双层缩套厚壁筒自增强残余应力分析

袁格侠 刘宏昭 赵迎祥 魏宏波

1.宝鸡文理学院，宝鸡，721016 2.西安理工大学，西安，710048

0 引言

超高压容器已经广泛应用于化工、食品、人造水晶、核工业、军事设备等领域。为了提高容器的承载能力和疲劳寿命，经常采用有效的多层缩套技术和自增强技术［1］。

尽管多层缩套技术和自增强技术都有各自的优点，但多层缩套技术受到层间最大过盈量的限制，自增强技术受材料包辛格效应（bauschinger effect，BE）的影响，以及在循环载荷作用下残余应力的松弛，使得这两种技术在进一步提高容器承压能力方面受到了限制。因此，将这两种技术相结合的多层组合筒体技术受到了研究者们越来越多的青睐［2－3］。两种技术的结合可进一步均化工作时筒壁上的应力分布，提高容器操作时的安全性［4］。

对于缩套与自增强技术相结合的双层筒体有两种处理顺序，一种是对内外筒先分别进行自增强处理，然后进行缩套，另一种是先缩套后再进行自增强处理［5］。

基于理想弹塑性材料模型，傅卫国等［6］研究了内筒先进行自增强，然后与外筒缩套的双层筒的最佳设计。李敬安等［7］研究了内外筒都先进行自增强，然后缩套的双层筒的优化设计，由于未考虑自增强残余应力对缩套过程的作用以及材料的包辛格效应，因此残余应力的计算误差较大。Parker等［8］基于可变材料模型，用数值方法研究了外筒进行自增强处理后与内筒缩套的双层筒残余应力的计算方法。

缩套后，内筒存在切向压缩应力，外筒存在切向拉伸应力，使自增强时材料的模型变得复杂化，即自增强处理时，内外筒之间存在高度非线性弹塑性接触问题，使得先缩套后再进行自增强处理的双层筒残余应力的计算变得十分复杂，难以得到其精确的解析解［9］。Parker等［10］用数值方法计算了该类双层筒的残余应力，主要研究了自增强百分比相同时缩套压力对残余应力的影响，以及筒体径比对疲劳寿命的影响。Lee等［11］的研究虽然给出了该类双层筒的残余应力解析解，但由于在计算自增强加载应力时未考虑缩套残余应力的存在，其计算结果误差较大。

本文利用ANSYS软件可以实现基于上一个载荷步的求解结果求解下一个载荷步的优势，在ANSYS平台上，利用其APDL语言开发了缩套双层筒自增强参数化接触有限元模型。考虑缩套应力对自增强处理时应力的影响，推导出了基于理想弹塑性材料力学模型的双层缩套厚壁筒残余应力解析解，并将本文解析解、Lee等［11］的解析解与有限元仿真值进行了对比研究。

1 双层厚壁筒接触分析模型的建立

为了便于对不同缩套过盈量和不同缩套半径的双层筒进行残余应力分析，基于ANSYS平台开发了双层筒的接触有限元参数化模型，并可自动完成网格划分和分析。

容器的几何模型为圆筒周向的1/4，将其内径、外径及长度进行参数化处理，单元类型选用3DSolid185。

内外筒的材料模型均为双线性随动硬化模型BKIN（bilinear kinematic hardening modle），它可以模拟材料的应变硬化和BE。该模型用弹性模量、泊松比、屈服极限和切线模量4个量来表征，为便于研究不同材料制成的筒体，对材料模型的表征量进行参数化处理［12］。

由于网格划分的疏密对分析结果有较大的影响，因此对网格划分也进行了参数化。这样可根据内外筒尺寸的大小及精度要求，控制网格的划分。厚壁圆筒是规则图形，采用映射划分。本文采用控制线段的份数来控制网格的疏密［12］。划分网格后的双层筒有限元模型如图1所示。内筒有25×10×4＝1000个单元，外筒有23×10×4＝920个单元。

双层缩套自增强筒的接触类型分析：在缩套过程中，外筒加热膨胀后，放入内筒，然后降温外筒收缩，外筒内表面与内筒外表面发生接触并产生弹性变形；在自增强加载过程中内筒通过接触面将力传递给外筒，实现体与体之间力的传递；在自增强卸载过程中，外筒弹性变形部分恢复，将外筒收缩力通过接触面又传递给内筒。在这3个过程中，接触面间都属于面与面之间的单向接触行为。内外筒的表面硬度和弹性模量相等或相差不大，其接触可视为“柔体—柔体”的“面—面”接触模型。

图1 双层厚壁筒有限元模型

创建接触对：根据以上分析，内外筒的接触为“柔体—柔体”的“面—面”接触模型。外筒内表面为目标面，单元类型为TARDE170，内筒外表面为接触面，单元类型为CONTA174。内外筒几何尺寸为实际尺寸，即包括初始相互渗透，许用接触面渗透量为0.0001mm。选用增广拉格朗日接触算法。

求解过程采用ANSYS的多载荷步法，其最大的优点就是可以实现基于上一个载荷步的求解结果求解下一个载荷步，这样就可对双层筒的缩套、自增强加载和自增强卸载过程的实际应力状态进行精确仿真。

通过以上步骤，建立了1/4 3D双层筒的参数化接触模型，并使用ANSYS的APDL语言编写了模型程序，自动实现模型建立和分析。

2 基于理想弹塑性材料模型的双层筒自增强残余应力解析解

缩套双层筒进行自增强处理时的横截面如图2所示。图中，ri、ro分别为双层筒内半径和外半径；rs为内外筒缩套半径；rc为自增强加载时的内筒屈服半径。

图2 双层厚壁筒横截面

现考虑存在缩套应力时，双层缩套筒体自增强处理后残余应力的解析解，并做如下假设：①假定材料不可压缩；②假定材料为理想弹塑性模型；③假定内筒为部分自增强；④不考虑外筒的塑性变形；⑤采用Mises屈服准则。

2.1 缩套应力分析

两筒进行缩套配合时，相当于内筒受外压，外筒受内压，根据Lamé公式［5］，内外筒应力分布为

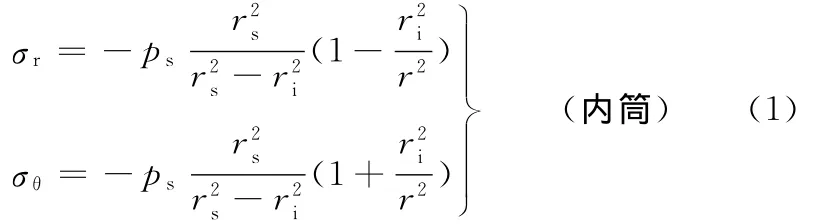
式中，σr、σθ分别为径向应力和周向应力；r为双层筒任意半径；ps为内外筒层间缩套压力；Δ为内外筒层间缩套过盈量；E1、E2分别为内外筒弹性模量；μ1、μ2分别为内外筒泊松比。

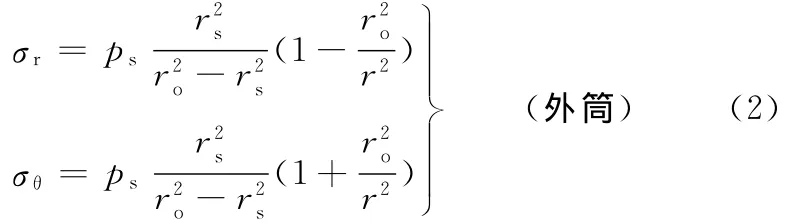
双层筒经缩套后，内筒存在压缩应力，外筒存在拉伸应力。自增强加载时，要使内筒屈服，首先要克服缩套后的压缩预应力；而外筒相反，由于存在拉伸预应力，自增强加载时更易屈服。亦即内筒抗拉强度增强，外筒抗拉强度减弱，并且半径不同，筒体的强度也不同，如图3所示。对于内筒，内壁强度最大，随着半径的增大，强度减小；对于外筒，内壁强度最小，随着半径的增大，强度也增大。

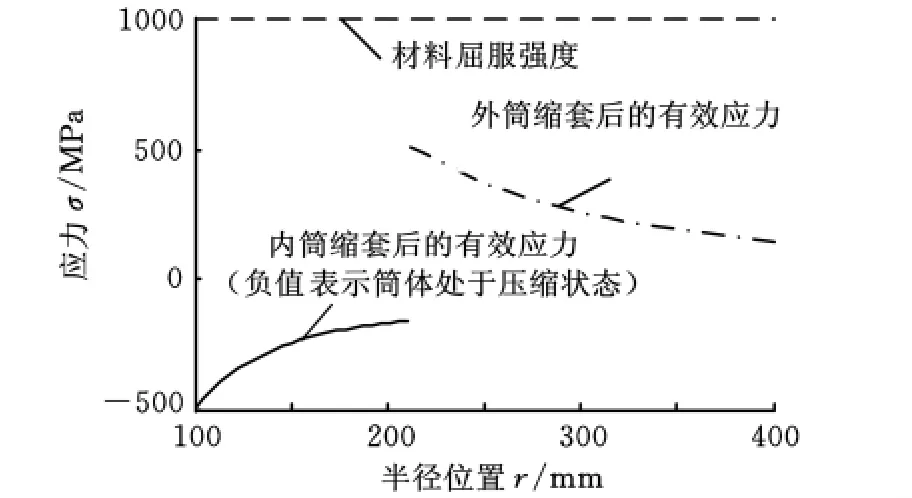
图3 缩套后的筒体强度

缩套后，内筒的有效应力可表示为

外筒的有效应力可表示为

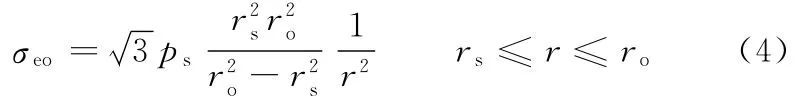
则此时内筒的拉伸强度可表示为

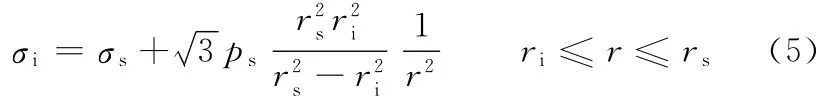
式中，σs为材料的屈服极限。

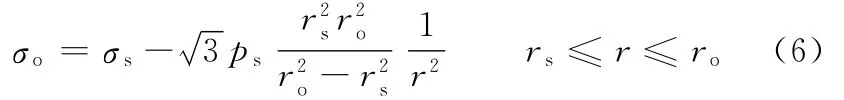
2.2 自增强加载时的应力分析

2.2.1 加载塑性区应力分析

在平面应变及材料不可压缩的情况下，根据Mises屈服准则，有

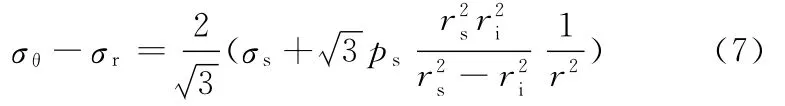
外筒拉伸强度可表示为

根据静力平衡方程，有

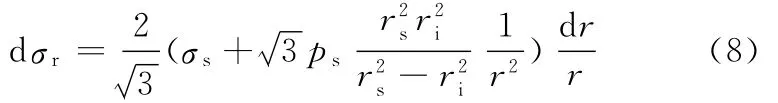
对上式从ri→r进行积分，可得

式中，p为任意半径r处的径向压力；pa为自增强压力。

在加载塑性区（ri≤r≤rc），径向与周向应力可表示为

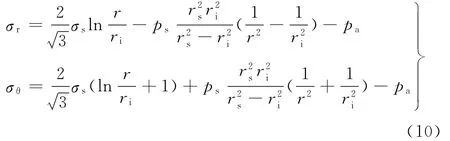
2.2.2 加载弹性区应力分析

当r＝rc时，径向应力的负值即为屈服半径处的有效压力pc，即

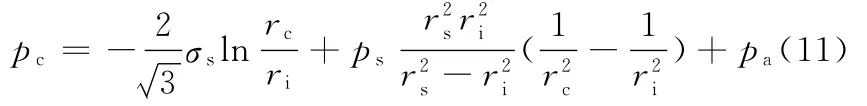
根据假定③和④，内筒弹性区及外层筒均处于弹性状态，则可将pc看作弹性区rc≤r≤ro的弹性极限压力。根据Mises屈服条件，有

根据连续性条件，式（11）与式（12）右边相等，则pa、ps与rc的关系式可表示为

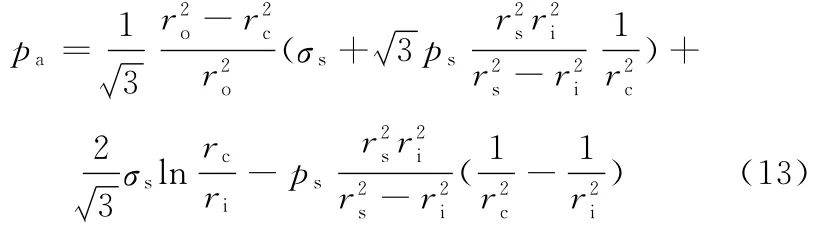
根据Lamé公式［5］，在弹性区rc≤r≤ro范围内，周向与径向应力可表示为

2.3 残余应力分析

假定卸载为完全弹性卸载，此时可把双层筒看做整体筒。在筒壁内产生的应力可用Lamé公式来确定，则卸压产生的应力可表示为

其中，任意半径r的变化范围为ri≤r≤ro。其双层筒的残余应力为缩套应力加上自增强加载应力再减去自增强卸载应力。

对于内筒，在加载塑性区ri≤r≤rc时的残余应力为

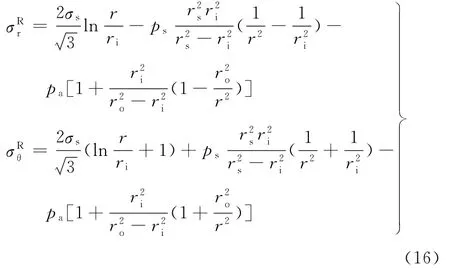
在加载弹性区rc≤r≤rs时的残余应力为

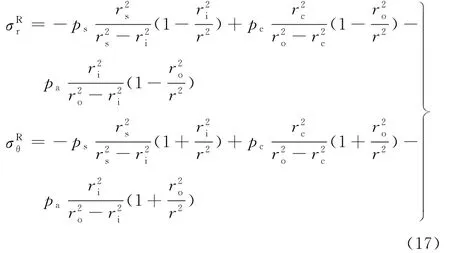
对于外筒，自增强加载时可认为处于弹性状态，其残余应力为

3 本文解析解、Lee解析解与仿真结果的比较

理想弹塑性材料模型是BKIN的特例，利用建立的有限元接触模型对某双层筒缩套与自增强过程进行仿真。仿真双层筒的结构参数如下：内径为100mm，外径为225mm，缩套半径为150mm，层间过盈量分别为0.2mm和0.3mm；自增强压力分别为700MPa和850MPa；内外筒弹性模量为198GPa，切向模量为0.1MPa，屈服极限为1000MPa。仿真结果与本文解析解、Lee［11］解析解如图4所示。

图4显示：本文残余应力解析解与有限元仿真值在内筒塑性区趋于一致，在弹性区和外筒塑性区略有差异，内筒屈服区半径略大于仿真屈服半径。Lee［11］的周向残余应力解析解在整个筒壁上都大于仿真值，且内筒与仿真值差异很大；随着过盈量的增大，内筒差异随之增大；随着自增强压力的增大，外筒的差异也随之增大。Lee［11］的径向残余应力与仿真值在缩套半径处差异最大，在内壁和外壁附近差异较小。

图4 本文解析解、仿真结果与Lee解析解［11］

本文解析解与仿真值的差别在于推导解析解时未考虑外筒缩套后强度的变化。Lee［11］解析解与仿真值的差别在于Lee［11］解析解在计算自增强加载时未考虑缩套预应力的存在，对缩套应力、加载应力和卸载应力进行了简单的叠加。实际上由于塑性变形的存在，合成残余应力与加载顺序有关，不再适用载荷独立作用时的叠加原理。自增强加载时，要使内筒屈服，首先要克服缩套后的压缩预应力；而外筒相反，由于拉伸预应力的存在，自增强加压时更易屈服，因此，内外筒残余应力仿真值都小于Lee［11］解析解。缩套过盈量愈大，内外筒缩套后的残余应力愈大，自增强加载时，对于内筒克服压缩残余应力所消耗的自增强压力愈多，因此仿真值内筒屈服半径小于Lee［11］解析解，这也使得过盈量愈大，Lee［11］解析解与仿真值的差异愈大。

4 结论

（1）基于ANSYS平台，使用APDL语言开发了双层缩套筒自增强参数化接触模型。模型的优点在于可以直接以层间过盈量为已知参数进行残余应力的计算。

（2）基于理想弹塑性材料力学模型和 Mises屈服准则，考虑缩套应力的影响，推导出双层缩套筒自增强残余应力解析解。

（3）将模型的分析值与 Lee［11］解析解及本文的解析解进行了比较，分析了双层筒缩套及自增强处理过程中的应力状态与加载次序的关系，从而论证了模型的准确性。

［1］Yuan Gexia，Liu Hongzhao，Wang Zhongmin.Optimum Design for Shrink－fit Multi－layer Vessels under Ultrahigh Pressure Using Different Materials［J］.Chinese Journal of Mechanical Engineering，2010，23（5）：582－589.

［2］Jahed H，Farshi B，Karimi M.Optimum Autofrettage and Shrink－fit Combination in Multi－layer Cylinders［J］.ASME J.Pressure Vessel Technology，2006，128（5）：196－200.

［3］Majzoobi G H，Farrahi G H，Pipelzadeh M K，et al.Experimental and Finite Element Prediction of Bursting Pressure in Compound Cylinders［J］.International Journal of Pressure Vessels and Piping，2004，81：889－896.

［4］Hanlon P C（EDT）.Compressor Handbook［M］.New York：McGraw－hill Professional Pub，2001.

［5］邵国华，魏兆灿.超高压容器［M］.北京：化学工业出版社，2002.

［6］傅卫国，吴光华.热套圆筒最佳过盈量和自增强压力简捷计算［J］.化工装备技术，1993，14（4）：22－25.

［7］李敬安.水炮的多层自增强高压腔筒的优化设计方法［J］.中国矿业学院学报，1986（1）：68－81.

［8］Parker A P.Bauschinger Effect Design Procedures for Compound Tubes Containing an Autofrettaged Layer［J］.ASME J.Pressure Vessel Technology，2001，123（2）：203－206.

［9］才鸿年，张玉诚，徐秉业，等.火炮身管自紧技术［M］.北京：兵器工业出版社，1997.

［10］Parker A P，Kendall D P.Residual Stresses and Lifetimes of Tubes Subjected to Shrink Fit prior to Autofrettage［J］.ASME J.Pressure Vessel Technology，2003，125（3）：282－286.

［11］Lee Eunyup，Lee Youngshin，Yang Quiming，et al.Autofrettage Process Analysis of a Compound Cylinder Based on the Elastic－perfectly Plastic and Strain Hardening Stress－strain Curve［J］.Journal of Mechanical Science and Technology，2009，23：3153－3160.

［12］袁格侠，刘宏昭，范彩霞，等.自增强超高压容器残余应力分析［J］.中国机械工程，2011，22（5）：536－540.