基于静力平衡原理的三维均质实体测量方法

甘 勇

桂林电子科技大学，桂林，541004

0 引言

随着现代制造技术、快速原形制造技术和反求工程技术的快速发展，研究开发高精度、低成本的三维实体无损测量技术有着越来越重要的现实意义。目前的三维实体测量方法主要有有损测量和无损测量两种，有损测量方法测量精度较高，但其测量速度慢、测量时间长，测量时要破坏被测零件，故测量成本较高，应用受到限制。目前应用较多的无损测量方法是光学测量方法，但该方法无法测量物体的内部轮廓，存在光学测量的盲点，且测量所得的数据点云庞大，杂乱无序，有的甚至残缺不全；另外，现有核磁共振成像和CT扫描方法能够测量物体的内部轮廓，但这两种方法的成本很高，对可测零件的尺寸有限制，测量精度低，特别是对被测实体的材料有限制［1－2］。目前基于浮力的三维测量方法可无损测量不溶于液体的均质实体，测量精度较高，能测量含有复杂内部轮廓的实体，但对于内部轮廓与外部不相通的均质实体也无法测量，且测量精度和可靠性受到液体的动态特性和不稳定性的影响［3－4］。国内外学者虽然在三维实体的测量技术方面做了大量的研究工作，也取得了不少的理论研究成果，并基于其研究成果开发了不少的工业产品，但到目前为止，还没有找到一种理想的三维实体的无损检测方法。针对这一技术难题，本文提出了一种基于静力平衡原理的三维实体无损检测方法，本方法应用分层原理，通过测量平衡系统中各力的变化值，根据空间力系平衡原理，推算出被测实体每层的质量及层中各微小单元体的质量和空间坐标，能对具有复杂内部轮廓的实体进行三维测量。

1 测量方法总体方案设计

在物体三维空间单元表示法中，空间单元体将空间分割成均匀的立方形网格，可以根据实体所占据的网格位置来定义物体的形状和大小。若此位置为物体所占据，即单元被填充，其质量视为单元质量1，称为实单元体；反之，空单元体以0表示。基于空间单元表示法研究均质实体，构建计算模型，可视其由单元正方体构成，采用基于二进制像素的三维重构方法，可取实单元体的质量为1，空单元体的质量为0，即所有像素值只能在（0，1）2个可能的离散值中选取，以此来表达空间图像单元体的有无［5－6］。本文测量方法根据杠杆平衡系统中力的变化实现无损分层测量，以杠杆平衡系统中力与力矩平衡和其与实体重量的关系为基础，通过按一定方向越过支点微小位移，测量杠杆平衡系统中实体每个不同位置的受力变化大小，求解被测实体各片层的质量和相应片层的重心坐标值。建立各片层质量和所含微小单元体的方程组及重心坐标方程组，通过智能计算求解方程组，获得各单元体的质量和其空间坐标值，进而对获得的点云数据进行图像重构。根据测量需求设计的总体方案原理图如图1所示，其测量系统主要由杠杆平衡系统、精密测力系统、装夹系统、精密运动系统及计算机组成。

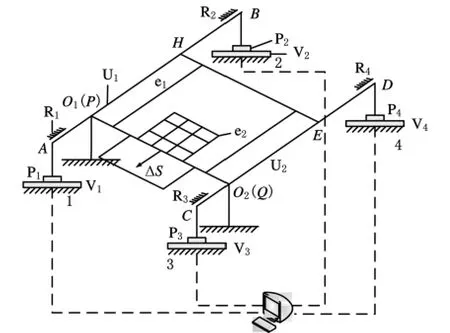
图1 三维均质实体无损测量方法原理图

杠杆平衡系统包括均质杠杆U1和U2、支撑平台e1和4个自动配重系统 P1、P2、P3、P4；杠杆U1的支点O1和杠杆U2的支点O2对称平衡地设置在相应的杠杆上；支撑平台e1与上述杠杆U1和杠杆U2之间通过4个固定力接触点P、Q、H和E相连接；其中，固定力接触点P和固定力接触点H位于杠杆U1上，且固定力接触点P与杠杆U1的支点O1重叠；固定力接触点Q和固定力接触点E位于杠杆U2上，且固定力接触点Q与杠杆U2的支点O2重叠；固定力接触点P和固定力接触点Q的连线与两杠杆U1和U2均垂直；固定力接触点H和固定力接触点E的连线也与两杠杆U1和U2均垂直；支撑平台e1在系统中本身的重力及力矩已知不变，并可以通过杠杆系统平衡掉；杠杆U1和杠杆U2的4个端点A、B、C和D上分别固定悬挂有一自动配重系统P1、P2、P3和P4。杠杆平衡系统快速调节杠杆U1和U2的平衡稳定，保护支点结构，维持系统平衡。为了提高测量精度，实现杠杆系统的快速稳定，以及保护精密测力仪器，杠杆U1和U2的4个端点A、B、C、D处各设有一限位器R1、R2、R3和R4。杠杆平衡系统的4个测力系统处各设有一个精密测力仪器V1、V2、V3和V4，该精密测力仪器的采集信号输出端均连接至计算机中。4个精密测力仪器用于被测实体e2发生位移时，实时测量各点的变化力。由于4个精密测力仪器的测量精度高、量程小，因此，设计了4个自动配重系统P1、P2、P3和P4进行配重，以解决其测量量程问题。装夹系统包括包容立方体机构，采用最小包容原则让被测实体e2装夹其中。精密运动系统的控制端与计算机相连，精密运动系统的动力输出端则与装夹系统相连，通过计算机指令控制包容有被测实体的装夹系统实现精密位移。

2 测量方法数学模型建立及求解分析

均质杠杆U1和U2分别对O1和O2点对称平衡，为简化计算，系统受力分析中均不计入。假设被测实体片层微小单元体为正方体且边长为ΔS，被测实体在支撑平台e1上，通过精密位移系统带动实现每次的微小位移ΔS，从而实现每个测量方向上各个片层按序移过支点，达到测量计算的目的。以支点O1和O2的连线中点O为坐标原点，将平行于杠杆的方向设为X轴方向，支点O1和O2的连线设为Y轴方向，垂直于X轴和Y轴的平面方向设为Z轴方向，建立空间三维坐标系。以计算被测实体在X轴测量方向上进行平移时所获得的片层质量和相应重心坐标为例，进行测量装置各部件受力分析，如图2所示。已知质量为M的被测实体所受的重力为G，将装夹有被测实体的包容立方体放置于杠杆平衡系统的支撑平台e1上，并让包容立方体所测片层方向的起始边缘与支点O1和O2的连线垂直相对，且将其状态设为被测实体的初始状态；通过调节自动配重系统，使杠杆平衡系统处于平衡稳定状态，同时，精密测力仪器测量并记录下该时刻杠杆平衡系统的4个测力点所受的力FA（0）、FB（0）、FC（0）和FD（0），并将其返回至计算机中。在初始位置，当杠杆U1平衡时（图2a），分别对支点O1和支点B进行受力分析，有

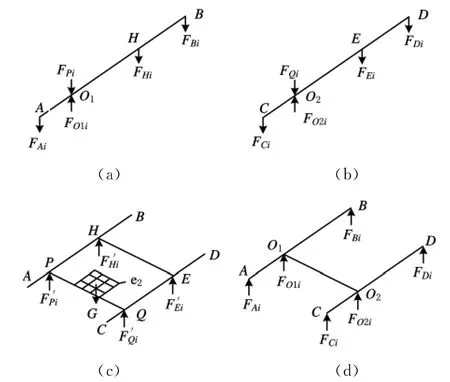
图2 测量装置各部件受力分析图

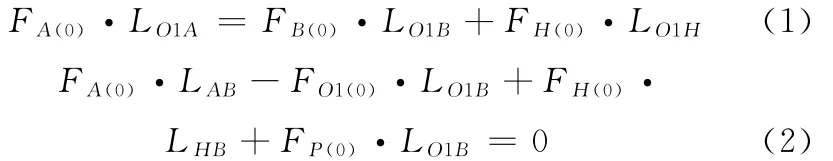
式 中，LO1A、LO1B、LO1H、LAB、LHB分别为 其下标两点 之间的距离。

在初始位置，当杠杆U2平衡时（图2b），对支点O2和支点D进行受力分析，有

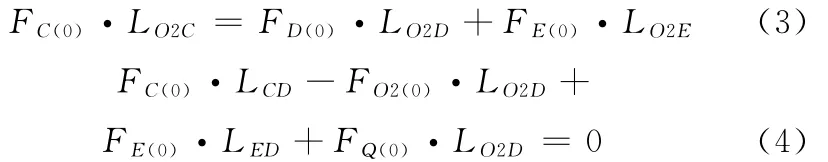
式中，LO2C、LO2D、LO2E、LCD、LED分别为 其下标两 点 之间的距离。

系统PQEH平衡时（图2c），对轴PQ进行受力分析，有

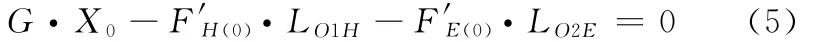
式中，X0为被测实体的重心坐标值；F′H（0）、F′E（0）分别为FH（0）、FE（0）的反 作 用 力，且 其 各 值 已 知 并 可 测 出；LO1H为其下标两点之间的距离。

系统PQEH平衡时，对轴EH进行受力分析，有

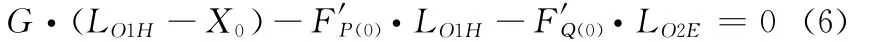
式中，F′P（0）、F′Q（0）分别为FP（0）、FQ（0）的反作用力，且其各值已知并可测出。

整个系统平衡时（图2d），对轴O1O2进行受力分析，有

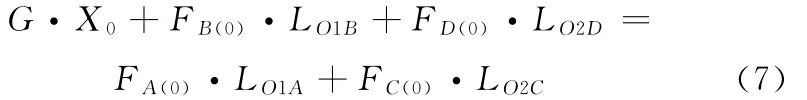
式中，LO1B、LO1A分别为其下标两点之间的距离。

计算机依据式（1）～式（7）联立求解出被测实体初始状态下的重心坐标值X0、支点O1和支点O2所受的力FO1（0）和FO2（0），以及固定力接触点P、Q、H和E所受的力FP（0）、FQ（0）、FH（0）和FE（0）。

保持被装夹系统的测量方向不变，让精密运动系统在计算机指令控制下带动装夹系统的包容立方体沿其X轴负方向每次平移ΔS后，通过调节自动配重系统使杠杆平衡系统处于平衡稳定状态，此时精密测力仪器测量出被测实体在第i（i＝1，2，…，n）层片层位置时杠杆平衡系统的4个测力点所受的力FA（i）、FB（i）、FC（i）和FD（i）。同上所述，杠杆U1平衡时，分别对支点O1和支点B进行受力分析；杠杆U2平衡时，分别对支点O2和支点D进行受力分析；系统PQEH平衡时，分别对轴PQ和对轴EH进行受力分析；整个系统平衡时，由于只有被测实体移动，其系统力矩变化相当于由片层质量引起，对轴O1O2进行受力分析，可列7个方程进行求解。计算机依据列出的静力平衡方程组联立求解出被测实体平移i次后第i层的片层重力Wi，以及支点O1和支点O2所受的力FO1（i）和FO2（i），固定力接触点P、Q、H和E所受的力FP（i）、FQ（i）、FH（i）和FE（i）。除去已测部分即未测部分的重心坐标Xi的方程为

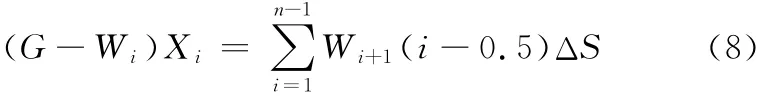
结合重力公式Wi＝miZg，即可获得被测实体在X轴测量方向上每片层的质量miZ，其中下标Z表示总质量。依次对被测实体的X轴方向、Y轴方向和Z轴方向，以及3个对角方向进行测量，且沿X轴、Y轴和Z轴3个方向测量时，每次平移微小单元体边长ΔS，从而获得被测实体在X轴、Y轴和Z轴3个测量方向上的每片层的质量和相应的重心坐标值。测量被测实体时，沿3个对角平面方向进行测量，每次平移ΔS时，就能获得被测实体在3个对角平面测量方向上的每片层的质量miZ和相应的重心坐标值，上述测量一共获得6个方向上的每片层的质量和相应的重心坐标值。

将包容立方体即被测实体分为n3个正方体的微小单元体，每个实微小单元体的质量为m，则第i层的总质量为

式中，mij为第i层第j个微小单元体，i＝1，2，…，n。

当被测实体e2移过第i层时，重心坐标方程为

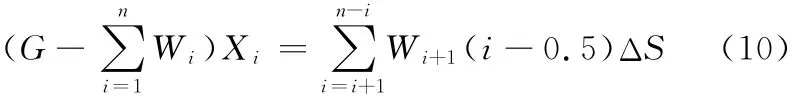
式中，Wi为第i层片层重力；Xi为未测部分的重心坐标。

若已知微小单元体的质量为m，则由微小单元体定义可知：所有微小单元体在实体空间只有两种情况存在，要么为实单元体，即质量为m；要么为空单元体，即不存在，质量为0。其数学表达式为

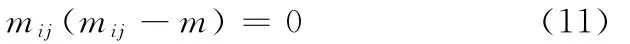
除可沿X、Y、Z3个方向进行测量外，通过改变被测实体的测量方向，还可沿各个对角平面的方向进行测量，即共有6个方向可供测量。故每一片层中的微小正方单元体的质量和可列一个线性方程，以及一个重心坐标计算线性方程。若一个实体共有N个微小正方单元体，当其在X、Y、Z3个方向上的每个单元体按坐标方向对齐时，一个坐标方向共可列出2N1/3个线性方程，则在X、Y、Z3个方向上进行测量时，共可列出6N1/3个线性方程；当沿各个对角平面方向进行测量时，共有6个方向，若每个方向只计片层质量方程，每片层一个方程，则共有6N1/3个方程；因此，在不同方向测量时，最少可列出12N1/3个线性方程。另外，还存在m1（m1—m）＝0，m2（m2—m）＝0，…，mN（mN－m）＝0等N个非线性方程，经过质量归一化处理以后，用这N＋12N1/3个方程优化求解N个未知数，可高精度地求得每一单元的质量，从而获得实单元质量的三维坐标值。

3 实验验证

根据测量总体方案进行初步实验，实验中的精密运动系统采用美国BAYSIDE LM系列运动平台，运动平台的重复定位精度达±5μm，其作用是控制定位平台，实现被测实体的精确位移。精密运动平台通过计算机控制指令控制被测实体按指定距离逐层位移。精密测力仪器采用瑞士梅特勒－托利多AB204－S型分析天平，其可读性和重复性均为0.1mg，具有去皮功能。它通过串口与计算机直接相连，用于测量杠杆平衡系统中力的变化。模拟实验测量采用图3所示的标准件模型，初步实验表明，本文实验测量片层质量的精度达到0.1mg，经智能运算测量的微小单元体的精度达到0.005%，测量重构精度达到±0.2mm，其重构点云图如图4所示。

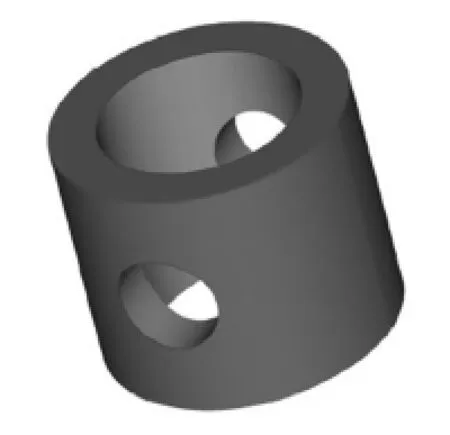
图3 被测标准件模型图

图4 转换后的点云图

4 结束语

本文测量方法所设计的测量平台不仅研制成本低、经济性好，而且可实现自动测量，其测量方法能够测量含有任意复杂内外轮廓的实体，且测量速度快、测量数据少、分层有序、重构简单；测量数据所列数学方程均有可靠成熟的解法，编程计算几乎不会给测量带来新的误差，其测量重构精度可以控制在0.2mm以内，基本满足生产实际中三维实体测量的工程要求。

［1］郭迎福，李兵，李鹏南，等.反求工程中测量技术综述［J］.矿山机械，2005，33（7）：75－77.

［2］金涛，陈建良，童水光.逆向工程技术研究进展［J］.中国机械工程，2002，13（16）：1430－1436.

［3］Gan Yong，Zhong Jing Ru，Gan Du Fen.Research on 3DNon－ destructive Measurement System Based on Homogeneous Entity［J］.Advanced Materials Research，2011，201/203：63－68.

［4］Gan Yong.Design for 3dEqual－density Entity Contour Digital Measurement Device［C］//Proceedings of the Second International Symposium on Test Automation ＆Instrumentation.Beijing，2008：2306－2310.

［5］Gan Yong，Sun Ning，Kong Qinghua，et al.Research on Method of 3DContour Digital Measurement for Entity［C］//Proceedings of ICMEM2007 International Conference on Mechanical Engineering and Mechanics.Wuxi，China，2007：395－400.

［6］甘勇，孙宁，孔庆华.面向均质实体的产品轮廓反求工程［J］.机械设计，2008（10）：8－11.