LMD时频分析方法的端点效应在旋转机械故障诊断中的影响

任达千 杨世锡 吴昭同 严拱标

1.浙江大学，杭州，310027 2.浙江机电职业技术学院，杭州，310053

0 引言

旋转机械故障诊断的目的是在早期发现潜在的故障。旋转机械在工作时会发生振动，通过对振动信号的检测和处理可以提取故障特征，并进一步确定故障类别。旋转机械故障诊断常用的信号处理方法有FFT、小波变换、Hilbert－Huang变换等［1］。

2005 年，Smith［2］提出了局域均值分解（local mean decomposition，LMD）算法，并首先将其应用于脑电图（EEG）信号的时频分析。与经验模态分解（empirical mode decomposition，EMD）类似，LMD也是以极值点定义包络线，但用滑动平均代替EMD方法中的3次样条插值。LMD的最终结果是一系列调频调幅信号，可以进一步用反余弦函数直接求得瞬时频率。由于端点附近的包络线无法正确获得，LMD算法同样存在端点效应。

为了解决LMD中出现的端点效应，本文提出了一种基于能量的端点效应评估方法，比较了LMD和EMD的端点效应。端点效应的严重程度与包络线的定义方法有关，由此提出一种镜像延拓极值点的端点效应抑制方法。将修正后的LMD方法应用于转子裂纹故障的诊断中，获得了较好的实验结果。为进一步抑制LMD的端点效应，可以考虑改进包络线的生成方法。

1 LMD基本算法

对信号的局域均值分解，首先需要确定原始信号x（t）所有的极值点，从左到右分别标记为n1，n2，…，其中，第i段的局域均值函数mi和局域包络函数ai分别为

再对局域均值函数和局域包络函数进行滑动平均，若相邻点的值相等，则再次滑动平均直到任何相邻点不再相等，即得到局部均值函数m11（t）和局域包络函数a11（t）。然后，将局部均值函数m11（t）从原始信号x（t）中分离出来，得到

再将h11（t）除以局域包络函数a11（t），以对h11（t）进行解调，得到

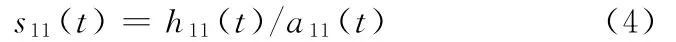
如果s11（t）相对应的局域包络函数不满足a12（t）＝1，则将s11（t）作为原始数据重复以上迭代过程，直到s1n（t）为一个纯调频信号，即－1≤s1n（t）≤1，它的局域包络函数满足a1（n＋1）（t）≈1。

最后把迭代过程中产生的所有局域包络线函数相乘便可以得到包络信号：

该包络信号即为乘积函数（production function，PF）的瞬时幅值。将包络信号a1（t）和纯调频信号s1n（t）相乘便可得到原始信号的第一个PF分量：

将PF1（t）从原始信号x（t）中分离出来，得到一个新的信号u1（t），将u1（t）作为原始数据重复以上步骤，循环k次，直到uk（t）的极值点少于等于1为止，x（t）分解为k个PF分量和uk（t）之和，即

式中，uk（t）为残余项；PFp（t）为包络信号ap（t）和纯调频信号sp（t）的乘积。

从上述计算方法可以看到，LMD分解是一个逐渐去除信号高频成分的过程。

2 端点效应的评价指标

实际存在的信号序列的长度总是有限的，在无法知道端点以外的信号的情况下，端点附近的局域均值函数和局域估计函数只能根据已知信号推测，不可避免地造成算法的误差。因此，LMD也受到端点效应的影响。文献［3］对EMD的端点效应做了定性描述，但没有给出端点效应的定量指标。

笔者认为，LMD的端点效应给分解结果添加了虚假成分，各PF的能量也会改变，因此可以通过比较LMD分解前后的信号能量，来评估端点效应的影响程度。

LMD分解的结果如下：

残余项uk（t）在这里也和PF一样参与计算。在实际计算中，为了便于比较，可以先计算原信号x（t）和LMD得到的各PF的均方根值（有效值）：式中，s（i）为需要计算有效值 的信号；n为信号的 采样点数。

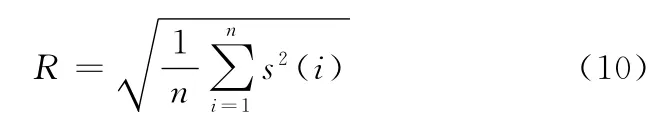
按式（10）比较各PF有效值的总和与原信号有效值，得到一个评价指标：

式中，R0为原信号有效值；Rp为第p个PF的有效值；Ru为残余项的有效值。

根据定义可知θ≥0，如果端点效应对LMD没有影响，则θ＝0。θ的值越大，说明端点效应的影响越严重。

3 LMD和EMD端点效应的比较

LMD和EMD的原理类似，两种分析方法均受到端点效应的影响。EMD分解受端点效应的影响很严重，如果没有适当的方法抑制端点效应，则虚假成分将从端点附近开始，逐渐“污染”整个信号序列。有时候，端点效应将导致EMD的结果完全不好用［3］。与EMD相比较，LMD的端点效应轻得多，处理起来也相对容易。LMD和EMD的端点效应对比如下：

（1）LMD信号端点附近未知包络线的长度比EMD的信号端点附近未知包络线的长度短。LMD和EMD的共同之处在于找出信号的极大值和极小值，然后由这些极值点来生成信号的包络线。端点以外的信号极值点是未知的，因此端点附近的包络线总是有一段是未知的，但是极值点生成包络线的方法有所不同，LMD未知的包络线长度比EMD的短。上述定义的局域均值函数和局域包络函数经简单的计算即可得信号的包络线，这里以局域均值函数为例说明。如图1所示，信号左端点的右边至第1个极值点（箭头所指）左边的局域均值函数是未知的。EMD的上包络线是对极大值点作3次样条插值，从第1个极大值点开始有定义；下包络线是对极小值点作3次样条插值，从第1个极小值点开始有定义；包络平均为上下包络之差，从第2个极值点开始有定义。因此，EMD的包络平均在第2个极值点（箭头所指）的左边是未知的。

图1 LMD和EMD端点附近包络线未知长度比较

（2）存在特殊的信号，LMD的分解结果几乎不受端点效应影响。在LMD分解过程中，如果端点同时也是极值点，那么端点作为一个极值点即可求出完整的局域均值函数和局域包络函数，端点效应可以基本得到消除。图2中余弦函数的表达式为

图2 余弦信号

图3所示为余弦信号的LMD分解结果（分解为乘积函数PF1和残余项R），残余项的幅值仅为原信号幅值的5.0×10－4左右，完全可以忽略。余弦信号的端点本身就是极值点，在LMD分解过程中，计算局域均值函数和局域包络函数将信号端点作为极值点，因此并不会带来误差，端点效应基本消除。

图3 余弦函数LMD分解结果

对于EMD，即使端点是极大值点或极小值点，信号的EMD分解结果依然受端点效应影响。余弦函数符合本征模函数（intrinsic mode function，IMF）的定义，EMD的分解结果应该就是原信号。实际分解结果如图4所示，IMF1最接近原信号，但是在端点附近发生了明显的变形，IMF2、IMF3、IMF4均是虚假的成分。

（3）LMD端点效应的扩散速度比EMD慢。LMD和EMD端点效应首先发生在端点附近，然后不断向内扩散，但是扩散的速度不一样。图5中，实线所示为正弦曲线，包络线应该为一直线，但由于端点效应，端点附近的包络线发生了变形。图5a中的虚线表示LMD算法的局域包络函数，端点效应的影响范围在箭头左侧，即端点以内的3个极值点。图5b中的虚线为EMD算法的上包络线（由3次样条函数插值得到），端点效应的影响范围在箭头左侧，即端点以内的5个极值点。

图4 余弦函数EMD分解结果

图5 LMD和EMD端点效应扩散速度比较

3 一种抑制LMD端点效应的延拓方法

本文提出的延拓方法，从本质上讲是一种镜像延拓，但只延拓一个极值点，而不是延拓一段信号。在每一次求局域均值函数和局域包络函数之前都重新延拓。这样延拓极值点之后，端点效应即可得到有效的抑制。

如图6所示，仿真信号是调幅信号和正弦信号之和，表达式如下：

如图7所示，小圆圈表示信号的极值点，以离端点最近的一个极值点为对称轴（点划线），将离端点次近的一个极值点向外延拓。在按式（1）、式（2）求局域均值函数和局域包络函数的时候，将这个延拓的极值点代入，即可求出信号完整的局域均值函数和局域包络函数。

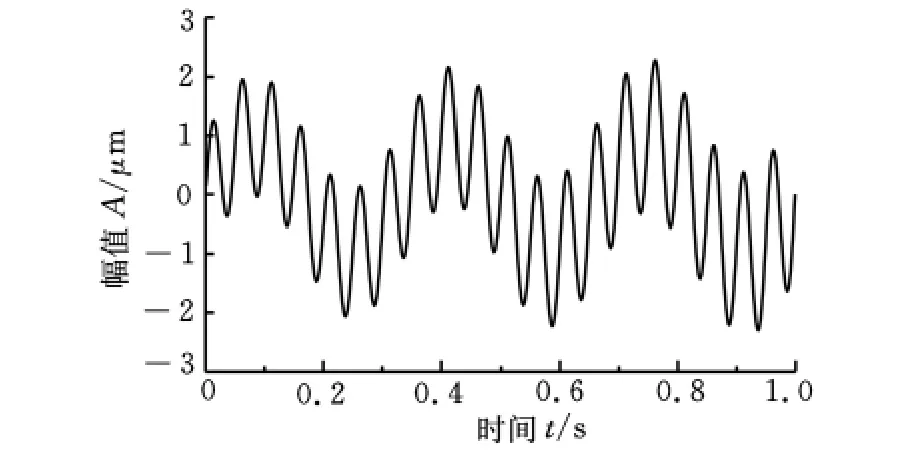
图6 仿真信号

图7 极值点延拓方法

没有应用端点效应抑制方法时，LMD分解结果如图8所示，分解结果共有7个乘积函数，可看到PF1为调幅信号，但是在端点附近有明显变形。PF2与正弦信号很相似。PF3～PF7和残余项的幅值较小，即可看做是LMD分解的误差成分。按式（11）计算可得评价指标θ＝0.029。

图8 未应用极值点延拓方法的LMD结果

对图6所示的仿真信号，应用延拓方法后再一次作LMD分解，结果如图9所示。仅有2个乘积函数和1个残余项，PF1和PF2仅在端点附近有非常轻微的变形，残余项的幅值很小，可以忽略。端点效应评价指标θ＝0.013。和图8所示的LMD分解结果相比，端点效应得到很好抑制。

图9 应用极值点延拓方法的LMD结果

4 裂纹转子故障诊断

Wang等［4］将LMD应用于转子碰摩和气流激振故障的特征提取，并认为LMD比EMD能更好地预测早期故障。

在转子系统中，裂纹故障具有突发、诊断困难、后果严重等特点。裂纹转子的振动机理尚不十分明确，而且小裂纹转子往往不发生剧烈的振动，因此裂纹故障十分隐蔽，难以识别。文献［5］指出，裂纹转子将引发弯扭耦合振动，扭转与弯曲振动的耦合是通过不平衡量来实现的，在裂纹较深和偏心较大时，扭转振动对弯曲振动的影响是比较大的。当转子系统产生扭振时，扭振信息以相位调制的形式存在于转子的振动信号中，形成调相信号，相位调制将改变振动信号的瞬时频率。因此，振动信号的瞬时频率可以作为裂纹转子的一种特征。

实验之前定制深裂纹转轴，首先利用线切割机在轴上指定位置切割出深度为直径50%的切槽，切槽宽度约为0.12mm，然后在切槽中嵌入厚度为0.10mm的薄金属片，使之形成近似的开闭裂纹，为防止薄金属片脱落，在薄金属片的其中一面涂上502胶水，使金属片与切槽单面粘合。如图10所示，裂纹与右端面的距离L＝100mm。振动信号波形和频谱如图11所示，采用定时采样方式，采样频率为3000Hz，轴频f0＝68.5Hz。

对转子裂纹故障信号做LMD分解，未处理端点效应和对极值点延拓的结果分别如图12所示。从图12可以看到，两者均分解为PF1～PF4，PF1的幅值最大，但是对极值点延拓之后，PF2～PF4的幅值下降。端点效应的评价指标θ从1.3×10－3下降到8.3×10－6。

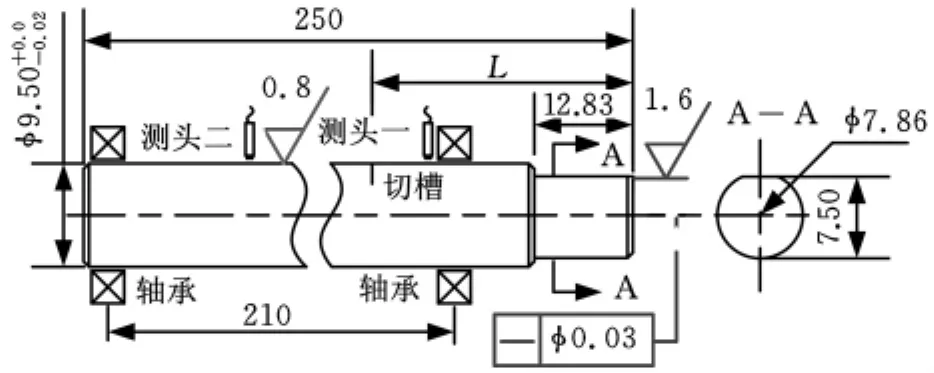
图10 转子裂纹加工示意图

图11 裂纹转子振动信号和幅值谱

基于LMD的时频谱如图13所示。边缘谱如图14所示，边缘谱的能量集中在轴频附近，没有明显的二倍频和高倍频，也可看到频率调制现象在频谱图和时频分析中的不同表现。信号经LMD分解以后，能量主要集中在PF1，应用“直接法”［6］对PF1求取瞬时频率，频率调制现象清晰可见，如图15所示。

由上述研究可知，裂纹转子的振动信号有明显的波内频率调制现象，边缘谱中二倍频则不明显。

5 结语

本文提出了一种基于能量的端点效应评价指标，对LMD的端点效应产生原因做了分析，并将其与EMD的端点效应进行了比较。因为包络线的定义方法不同，端点附近未知的包络线长度较短，存在特殊信号，LMD分解结果几乎不受端点效应影响，且LMD端点效应的扩散速度比EMD慢，因此LMD的端点效应相对较轻。提出的一种端点镜像延拓的端点效应抑制方法经仿真验证，能很好地抑制LMD的端点效应。应用LMD对转子裂纹故障做了实验研究，发现LMD方法能提取出转子裂纹故障的特征，取得较满意结果。

图12 裂纹转子振动信号LMD分解结果

图13 裂纹转子振动信号基于LMD的时频谱

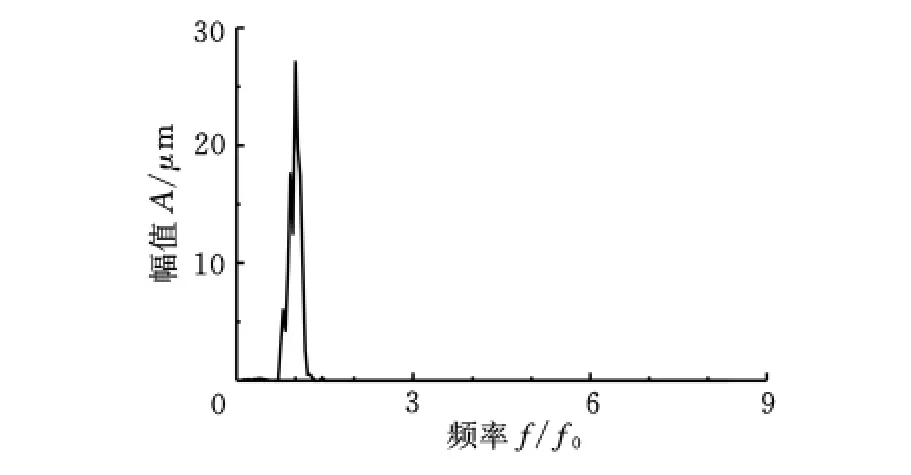
图14 裂纹转子振动信号边缘谱

图15 对裂纹转子振动信号PF1求得的瞬时频率

［1］褚福磊，彭志科，冯志鹏，等.机械故障诊断中的现代信号处理方法［M］.北京：科学出版社，2009.

［2］Smith J S.The Local Mean Decomposition and Its Application to EEG Perception Data［J］.J.R.Soc.Interface，2005，2（5）：443－454.

［3］Huang N E，Shen Zheng，Long S R，et al.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non－stationary Time Series Analysis［J］.Proceedings of Royal Society A，1998，454（1701）：903－995.

［4］Wang Yanxue，He Zhengjia，Zi Yanyang.A Comparative Study on the Local Mean Decomposition and Empirical Mode Decomposition and Their Applications to Rotating Machinery Health Diagnosis［J］.Journal of Vibration and Acoustics，2010，132（2）：10.1115/1.4000770.

［5］杨正茂，肖锡武.裂纹转子弯扭耦合振动的理论研究［J］.华中科技大学学报（自然科学版），2002，30（6）：1－3.

［6］任达千，杨世锡，吴昭同，等.基于LMD的信号瞬时频率求取方法及实验［J］.浙江大学学报（工学版），2009，43（3）：523－528.