基于混合遗传算法的混流混合车间协同调度问题
2012-07-25李修琳鲁建厦柴国钟汤洪涛蒋玲玲
李修琳 鲁建厦 柴国钟 汤洪涛 蒋玲玲
浙江工业大学,杭州,310032
0 引言
在实际离散制造过程中,产品生产过程一般包括零件加工、部件装配和产品总装,其生产形式是作业车间和流水车间集成的混流混合车间模式。零件加工车间、部件装配车间与产品总装车间在计划制定、物料供应和调度执行方面都紧密相关。生产调度及其执行过程中,优化多集中于单一车间而忽略与其他车间的关联影响。如零件加工车间往往以产品切换费用、换模费用的最少等目标来安排生产,而部件装配车间、产品总装车间以生产周期最短等目标来安排生产,从而导致零件的加工进度跟后续的部件装配或者产品总装不相匹配,造成大量的缓冲区在制品库存,拉长了产品的整个生产周期,影响了生产流程化,无法达到系统最优。在混流生产模式下,这种情况尤为严重。因此,对于具有自制件的混流装配生产过程,必须从整体优化的角度出发,建立多车间的集成调度。
目前的研究主要针对零部件车间的加工调度或者零部件装配车间的排序调度等单一车间展开,对作业车间和流水车间的集成研究较少。Lee等[1]研究了三机装配型流水车间的调度问题,优化目标是最小化最大完工时间。文献[2-3]以最小化最大完工时间为优化目标,研究了带装配操作的两机流水车间调度问题。上述研究考虑的加工装配车间过于简单,只是将装配车间看成一台机器,研究的是单品种生产,且没有考虑各个车间之间的缓冲区在制品库存问题。王炳刚等[4-5]研究了带有限缓冲区的流水车间集成调度问题,建立了带并行机的流水部件线和单机流水总装线的集成调度模型,有效弥补了上述研究的不足,但仍没有关于作业车间与流水车间的混合模型。
1 问题描述
1.1 混流混合车间模型
本文所要研究的混流混合车间由三部分组成:第一部分为加工零件的作业车间,以批为单位进行生产;第二部分为装配部件的流水车间,以个为单位进行装配;第三部分为产品总装的流水车间,以个为单位进行装配。图1所示为所要研究的混流混合车间简化模型。

图1 混流混合车间简化模型
混流混合车间主要有以下特点:①混合车间生产不同品种的产品,且以混流生产方式组织生产;②零件加工车间、部件装配车间、产品总装车间之间由缓冲区连接;③零件加工车间为部件装配车间和产品总装车间提供物料,部件装配车间为产品总装车间提供物料;④各生产单元间通过物料约束关联,适当的缓冲设置可在生产流畅的情况下减少生产运作成本;⑤同时具有作业车间调度和流水车间调度问题的各种约束条件;⑥加工零件的作业车间以批为单位进行生产,部件装配、产品总装的流水车间以个为单位进行生产。
1.2 混流混合车间调度模型的构建
在混流混合生产系统中,各生产单元是相对独立的子系统,虽然具有不同的生产特征和优化目标,但仍相互依赖、相互制约。在生产调度过程中,各生产单元通常单独制定调度方案,单方面进行各自生产单元的优化,虽然达到各自的生产目标,但却以其他单元生产目标的弱化为代价,使生产内部不协调,经常出现需要的零部件未生产,而暂时不需要的零部件却大量堆积,产生大量在制品库存,严重影响了生产物流的流畅性,增加了企业生产、场地和资源的成本。因此,集成调度零件加工车间、部件装配车间、产品总装车间,并控制其之间的缓冲区在制品库存具有非常重要的实际意义。针对混流混合车间调度问题,建立以最小化缓冲区在制品库存成本为目标的优化模型。
混流混合车间调度问题可描述为,以零件加工车间、部件装配车间和产品总装车间组成的三段生产系统中,零件加工车间有m台机器,加工n种零件,部件装配车间有l1个装配工位,生产r1种部件;产品总装车间有l2个装配工位,生产r2种产品,生产调度旨在安排各工件在各设备和工位上的生产顺序,实现既定目标的优化。为了便于研究混流混合车间调度问题,给出以下假设条件:
(1)只对自制件在流水车间装配的调度进行研究,外购外协件不在考虑范围内。
(2)若零件加工车间为部件装配车间、产品总装车间的装配工位加工了一批零件,或者部件装配车间为产品总装车间的装配工位加工了某种部件,而装配工位不需要,即装配工位已有的零部件能够满足装配所需要的数量,或者已加工的零部件不是装配工位所需要的类型,则将此批零件或者此种部件暂存在缓冲区,反之向相应工位配送,其中的配送时间假定为零。
(3)作业车间内零件的工序之间有工艺约束,不同零件之间不存在工艺约束。
(4)在零时刻,所有的零件都可以被加工。
(5)在零时刻,所有的机器及装配工位都已经准备就绪。
(6)工序加工时间已经包含了工序的准备时间和搬运时间。
目标函数为最小化缓冲区在制品库存成本,模型如下:

式中,Ai为一批自制零件i所占的面积;Ax为一个部件x所占的面积;Ci为单位面积的零件i在缓冲区存放单位时间所占用的成本;Cx为单位面积的部件x在缓冲区存放单位时间所占用的成本;Ti为一批零件i被加工出来的完工时刻;T′i为此批零件被下游领走的时刻;Tx为一个部件x被生产出来的完工时刻;T′x为此部件被下游领走的时刻。
1.2 模型约束
1.2.1 工艺顺序约束
(1)零件加工车间约束。自制零件的前一道工序加工完成后,才能加工后一道工序,其约束表达式为

式中,Eij、Eih分别为零件Ni在机器Mj和Mh上加工的完工时刻;D是一个足够大正数,作为对约束违背的惩罚系数;tij为一批自制零件Ni在机器Mj加工所需要的时间。
(2)部件装配车间约束。部件的前一道工序装配完成后,才能装配后一道工序,其约束表达式为

式中,Exk、ExH分别为部件装配流水车间中部件x在第k个装配工位和第H个装配工位上的完工时刻;txk为一个部件x在第k个装配工位上装配所需要的时间。
(3)产品总装车间约束。产品的前一道工序装配完成后,才能装配后一道工序,其约束表达式为

式中,Eys、EyK分别为产品总装流水车间产品y在第s个装配工位和第K个装配工位上的完工时刻;tys为一个产品y在第s个装配工位上装配所需要的时间。
1.2.2 资源约束
(1)零件加工作业车间约束。在同一台机器上,一批零件的加工任务完成后,方能开始下一批加工,其约束表达式为

(2)部件装配流水车间约束。在同一个装配工位上,一个装配任务完成后,方能开始下一个任务,其约束表达式为

(3)产品总装流水车间约束。在同一个装配工位上,一个装配任务完成后,方能开始下一个任务,其约束表达式为
1.2.3 时间约束
(1)部件装配完工时间等于该部件进入工位的时间与装配操作时间以及在该工位的等待时间之和:

式中,Bxk为部件装配流水车间中部件x在装配工位k上可以开始装配的时刻,即表示部件x已经完成前一道工序的装配任务,装配工位k已经完成前一个部件的装配任务;Δxk为部件装配车间部件x在装配工位k上开始装配的延迟时间(停工待料时间);Qikt、Qikt′分别为t和t′时刻部件装配车间的装配工位k含有的自制零件i的数量;Oixk为t时刻部件装配车间部件x在装配工位k上装配时需要的自制零件i的数量;txk为一个部件x在第k个装配工位上装配所需要的时间。
(2)总装配件完工时间等于该产品进入工位的时间与装配操作时间以及在该工位的等待时间之和:

式中,Bys为产品总装流水车间产品y在装配工位s上可以开始装配的时刻,即表示产品y已经完成前一道工序的装配任务,装配工位s已经完成前一个产品的装配任务;Δys为产品总装流水车间产品y在装配工位s上开始装配的延迟时间(停工待料时间);Qist为t时刻产品总装车间装配工位s含有自制零件i的数量;Qiys为产品总装车间的产品y在装配工位s进行装配时需要的自制零件i的数量;Qxst为t时刻产品总装车间装配工位s含有部件x的数量(前面已经假设零部件从缓冲区配送到装配工位的时间为零,此时的数量为装配工位和缓冲区中数量的总和);Qxys为产品总装车间产品y在装配工位s上进行装配时需要部件x的数量;tys为一个产品y在第s个装配工位上装配所需要的时间。
模型中,aihj、bigj、a′xHk、b′xgk、a′yKs、b′ygs为指示变量,aihj、a′xHk、a′yKs为0,表明该调度方案不符合工艺顺序约束要求;bigj、b′xgk、b′ygs为0,表明该调度方案不符合资源约束要求。
2 混合遗传算法求解调度模型
遗传算法是求解组合优化问题的优秀算法,具有良好的全局搜索能力,针对混流混合车间调度解空间大的特征,具有较好的优化效果。目前,GA在装配线和作业车间独立优化问题上已取得良好的应用效果[6-8],与模板退火算法结合的混合算法也取得了良好效果[9]。因此,将遗传算法作为算法主流程。为提高局部搜索能力,在遗传算法的流程中嵌入模拟退火算法,建立了一种混合算法。模拟退火算法可以对每一代种群中最好的部分个体执行退火操作,有效提高邻域搜索效率,弥补遗传算法在局部搜索方面的不足。
2.1 算法流程
图2所示为混合算法的主要流程。相关说明如下:①算法包含5个基本参数(种群规模N、最大迭代次数M、初始温度θ0、终止温度θend、退温系数λ),随机产生规模为N的初始种群P(T),初始代数T=0;②适应度计算,计算种群中每个个体的适应度值;③对种群进行选择、交叉、变异操作,产生新一代种群P(T+1),并将种群中具有最佳适应度值的个体集合作为P(x);④对种群P(x)进行模拟退火操作;⑤判断迭代条件,如果满足则输出最优解,并终止算法。

图2 混合算法的主要流程
2.2 算法详细设计
2.2.1 编码
混流混合车间调度问题的编码规则如下:根据给定的生产任务,先将产品级分解为部件级、零件级,然后根据各种零件的数量、比例和加工批量确定零件生产车间的零件生产批量;部件装配车间和产品总装车间是流水车间,取各产品数量的最大公约数,并通过各产品数量除以该值确定各部分的最小生产循环,对一个循环中的产品装配工序进行编号;编码分成三部分,其中,第一部分为零件加工车间零件的批量编号,第二部分为部件装配车间的部件编号,第三部分是产品总装车间的产品编号。为了修正操作运算后产生的非法解,分别对零件加工工序和装配工序的对应编号从小到大进行重排序,从而保证产生的新种群都为合法解。
示例:产品总装流水车间要生产10个A、10个B;装配1个产品A需要1个部件U、1个零件a和1个零件b;装配1个产品B需要1个部件V、1个零件a和1个零件c;装配1个部件U需要1个零件d,装配1个部件V需要1个零件e。其中,各零件加工批量为10。假定零件加工作业车间由4台设备(M1、M2、M3、M4)组成,加工零件a、b、c、d、e。各零件工序作业时间及作业顺序如表1所示。表1中,逗号左侧的数字为加工时间(s),逗号右侧的数字为加工工序的顺序号。
由已知条件可以知道,生产10个产品A、10个产品B需要零件20个a、10个b、10个c、10个d、10个e,需要部件10个U、10个V,即零件加工作业车间需要加工2批a、1批b、1批c、1批d、1批e。零件序列为[a,a,b,c,d,e],分别对各零件工序进行编号,如表2所示。表2中,a出现2次,表示零件a的2个不同批次;部件装配流水车间需要装配10个U、10个V,则部件装配流水车间的最小生产循环为1个U、1个V,对其进行编号,如UV为1个最小生产循环;产品总装流水车间的最小生产循环为1个产品A和1个产品B,如AB为一个最小生产循环。

表1 工序作业时间及作业顺序表

表2 工序顺序编号表
图3所示为一条染色体编码。染色体采用三段式的编码方法,S1段为作业车间编码,S2段为部件车间编码,S3段为装配车间编码。其中,编号1~4的码值为1,该码值按照顺序分别代表第一个工件即工件a的4个工序。采用该编码方法可在交叉变异操作时避免非法染色体的产生。
2.2.2 适应度函数
由于优化目标为缓冲区在制品成本最小化,因此将目标函数适当改变作为适应度函数:

2.2.3 种群选择
算法根据适应度函数值采用赌轮盘法选择个体遗传到下一代群体中。
2.2.4 交叉与变异
鉴于混流混合车间调度问题特点,零件加工车间、部件装配车间、产品总装车间的各段染色体编码进行各自独立的交叉和变异操作。交叉方法采用单点交叉;变异采用交换变异方法,即交换两个随机位置上的基因[10]。
2.2.5 模拟退火算法

图3 染色体编码
为提高精英群体的质量,算法采用变温度的模拟退火算法对每代最优的群体P(x)执行模拟退火操作SA。最优解x操作后得到的新解x′=SA(x)。如果x′优于x则保留新解,否则以概率exp(-Δθ′/θ)接受新解,其中,θ为当前温度,Δθ′为原解与新解的适应度差。新解的产生通过交换变异的方法,分别对三段编码各自进行交叉,防止不同类调度工件的串码,从而保证染色体的合法性。算法进程由初始温度θ0、终止温度θend、退温系数λ控制。模拟退火算法增强了个体的局部搜索能力,但增加了时间和计算成本,为平衡算法效率,算法采用变温度的温度适应算法,其中,当前温度为

式中,T为当前迭代代数;ceil(*)表示对括号中内容向下取整。
为保证迭代末期的有效温度,设定θ′e不小于1。在变温度的支持下,算法初期可提高算法的全局寻优能力,算法后期可加快算法的收敛速度,从总体上提高了算法的执行效率。
2.2.6 终止准则
以预先设定的最大进化代数M为终止条件。
3 实例验证
混流混合车间在生产中应用广泛,现以某冰箱制造企业为例对模型和算法进行验证。该生产系统由零件加工车间、部件装配车间和一条总装配线组成。零件加工车间的主要任务为生产8种自制零件。自制件集合为{N1,N2,…,N8},作业车间机器集合为{M1,M2,…,M10}。自制件在各机器上的加工以批为单位,工艺顺序及加工时间如表3所示。

表3 自制件工艺顺序及加工时间
部件装配车间主要负责门体A、B的装配,其装配工艺与时间如表4所示。

表4 部件装配工序的作业时间 s
产品总装流水车间共有33个装配工位,流转产品 Q1、Q2、Q3、Q4,对应的装配工序作业时间如表5所示。

表5 总装装配工序的作业时间 s
表6为零部件对应的产品需求矩阵,对应值为所需数量。

表6 产品需求矩阵

表7 各零部件滞留单位成本 元/(d·m2)

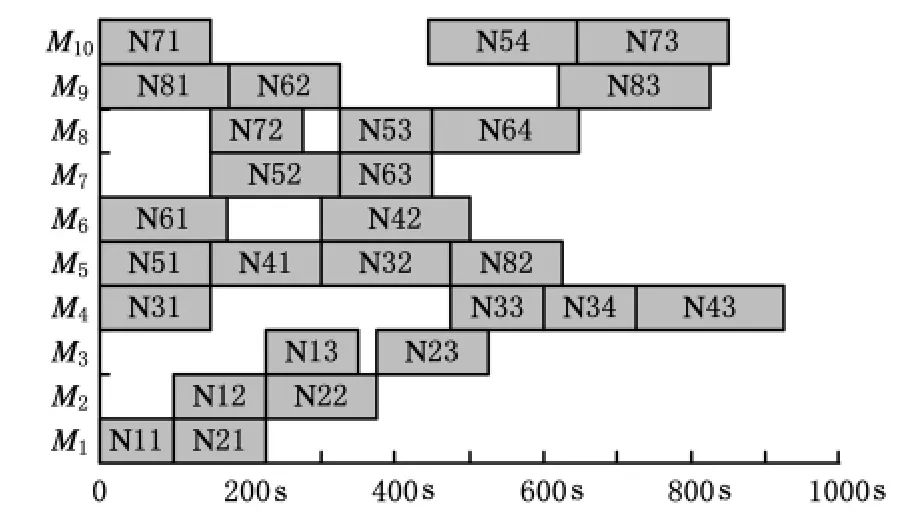
图4 零件加工调度甘特图
4 结语
混流混合车间是离散生产中常见的生产组织方式,本文描述了混流混合车间调度问题的特点,建立了混流混合车间缓冲区在制品成本最小优化模型,给出了集成模拟退火算法的混合遗传算法,并对模型进行求解,最后通过某冰箱企业混流混合车间调度问题的实例研究,验证了所建模型和算法的有效性。文中仅针对混流混合车间做了初步的集成调度研究,但混流混合车间作为一种混合生产系统,影响因素多,并涉及多个优化目标,后续研究应发掘影响生产系统的瓶颈因素,实现各子系统的多目标协调调度。
[1]Lee C Y,Cheng T C E,Lin B M T.Minimizing the Makespan in the 3-Machine Assembly-type Flow Shop Scheduling Problem[J].Management Science,1993,39(5):616-625.
[2]Cheng T C E,Wang G.Scheduling the Fabrication and Assembly of Components in a Two-machine Flow Shop[J].IIE Transactions,1999,31(2):135-143.
[3]Lin B M T,Cheng T C E.Fabrication and Assembly Scheduling in a Two-machine Flow Shop[J].IIE Transactions,2002,34(11):1015-1020.
[4]王炳刚,饶运清,邵新宇,等.基于多目标遗传算法的混流加工/装配系统排序问题研究[J].中国机械工程,2009,20(12):1434-1438.
[5]王炳刚.混流加工/装配系统集成优化研究[J].机械工程学报,2010,46(17):114-122.
[6]苏平,于兆勤.基于混合遗传算法的混合装配线排序问题研究[J].计算机集成制造系统,2008,14(5):1001-1007.
[7]Chul J H,Kim Y.A Genetic Algorithm for Multiple Objective Sequencing Problems in Mixed Model Assembly Lines[J].Computers and Research,1998,25(7):675-690.
[8]袁坤,朱剑英.一种求解多目标柔性Job Shop调度的改进遗传算法[J].中国机械工程,2007,18(2):156-160.
[9]鲁建厦,蒋玲玲,李修琳.基于混合粒子群算法求解装配线第二类平衡问题[J].中国机械工程,2010,21(4):420-424.
[10]刘民,吴澄.制造过程智能优化调度算法及其应用[M].北京:国防工业出版社,2008.
