并联机构驱动奇异的分层递阶滑模控制方法

刘延斌 郭志佳 韩建海

河南科技大学，洛阳，471003

0 引言

并联机构具有刚度大、承载能力强、误差小、精度高、自重负荷比小、动力性能好、控制容易等一系列优点，在性能和应用上弥补了串联机构的不足，因此在复杂曲面的焊接、喷涂、加工、测量等领域有广阔的应用前景。但目前真正应用到这些领域的并联机构并不多，其原因之一就是绝大多数并联机构（除少数无奇异并联机构外）都存在驱动奇异问题。驱动奇异发生在工作空间内部，位形复杂，当并联机构执行复杂曲面的焊接、喷涂、加工、测量等任务时，势必要进行大范围的连续工作空间轨迹运动，因此不可避免地会以任意状态自由地穿越工作空间内部的驱动奇异位置（奇异点），然而并联机构处于驱动奇异位置时，动平台某些方向上的运动将失去约束而失控，导致任务空间的运动控制精度难以保证，驱动输入（驱动力/力矩）也迅速无限增大，直接影响工作质量。

目前关于并联机构驱动奇异的运动控制研究可归结为低速情况下的运动学控制和高速情况下的动力学控制两个层面。在运动学控制研究层面：Nenchev等［1］提出了一种基于轨迹参数化的运动学控制方法，首先假定机构运动轨迹可参数化，然后在Lyapunov稳定设计理论的框架下运用伪逆方法获得轨迹参数和驱动速度控制律，但该方法的前提是轨迹可参数化；王玉新等［2］提出了一种扰动函数法，通过对机构输入参数施加扰动量使机构保持构型通过奇异位置。在动力学控制研究层面：Ider［3］提出了一种与动力学方程相容的路径规划方法，使机构沿此路径稳定地穿越奇异位置，但其缺点是限制了穿越奇异位置的任意性，而且控制力矩需要由动力学方程的高阶导数信息获得，计算稍显复杂；Jui等［4］提出了一种基于轨迹参数化的动力学控制方法，首先假定机构运动轨迹可参数化，然后根据奇异区内的某些稳定条件对轨迹参数进行规划，再结合伪逆方法获得驱动力控制律，其缺点同样是限制了穿越奇异位置的任意性；Briot等［5］提出了一种基于最优动力学条件的路径规划方法，可使机构沿此路径稳定地通过奇异位置，其缺点仍然是限制了穿越奇异位置的任意性；Kao等［6］提出了一种阻尼最小二乘法，其思想是当机构通过奇异位置时，对失秩的雅可比矩阵通过运用伪逆方法和引入阻尼项进行数学处理，以获得奇异鲁棒性和控制精确性折衷的近似解。

本文引入滑模控制理论，分别基于分层递阶结构的滑模控制方法［7－9］和基于伪逆的滑模控制方法设计了运动控制器，并通过仿真进行了分析和验证。

1 自由度分析

图1所示的3－RPR型平面并联机构含3个分支，每个分支由2个转动副（R副）和1个移动副（P副）组成，DFE为动平台，ACB为基平台，三个P副为驱动副，a为DF的长度，b为FE的长度，c为AC的长度。

图1 3－RPR型平面并联机构及其结构参数示意图

设定一个动平台坐标系O′UVW，原点与DE的中点重合，U轴与直线DE重合，V轴与直线DE垂直，W轴与6个R副轴线平行。再设定一个参考坐标系OXYZ，当机构处于中位时，原点与坐标系O′UVW的原点重合，轴X、Y、Z分别平行于轴U、V、W。

可见，3－RPR型平面并联机构的动平台相对基平台有3个自由度：绕Z轴的旋转和沿X轴、Y轴的平移。

2 奇异分析

2.1 约束奇异分析

2.2 支链奇异分析

2.3 驱动奇异分析

图2 3－RPR平面并联机构的七种可能驱动奇异位形

3 动力学建模

首先确定系统的位形坐标：

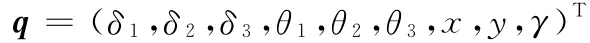
式中，δ1、δ2、δ3为3个驱动副的伸缩量；θ1、θ2、θ3为3条支链相对于基平台的转角；（x，y，γ）为动平台在参考系中的位姿坐标。

则可建立如下的6个运动学方程：

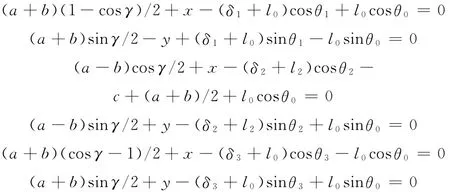
将x、y、γ视为独立变量，则根据上面的运动学方程可得到非独立变量δ1、δ2、δ3、θ1、θ2、θ3关于独立变量的表达式：

系统的总动能为

系统的总势能为

式中，mm、Jm分别为动平台的质量和相对质心的转动惯量；mi1、Ji1分别为第i条支链的下伸缩杆的质量和相对于基平台连接的铰点的转动惯量；mi2、Ji2分别为第i条支链的上伸缩杆的质量和相对质心的转动惯量；li为第i条支链的中位长度，l0＝l1＝l3；hi1为第i条支链的下伸缩杆的质心到与基平台连接的铰点的距离；hi2为第i条支链的上伸缩杆的质心到与动平台连接的铰点的距离。

将非独立变量δ1、δ2、δ3、θ1、θ2、θ3的代数表达式及其1阶微分代入式（1）、式（2）中，则根据拉格朗日方程可得如下形式的动力学模型：

式中，u为驱动输入。

4 驱动奇异运动控制

4.1 基于分层递阶结构的滑模控制

通过奇异分析可知，并联机构处于图2a～图2f所示的奇异位形时，均仅有一个运动失去约束，此时的雅可比矩阵的秩应为2，因此在奇异位置X0，JT（X0）可通过奇异值分解表达成如下形式：

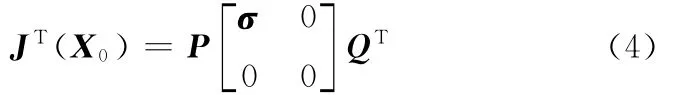
式中，P、Q均为正交变换矩阵；σ为对角阵，σ＝diag（σ1，σ2）；σ1、σ2为奇异值。

在奇异位置X0的邻域Ω内，有

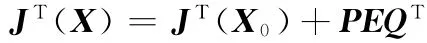
式中，E为小参数对角阵，E＝diag（ε1，ε2，ε3）。

对于式（3）的右端则有

令τ＝QTu，并将式（4）代入式（5）得

由于E为小参数矩阵，因此可将Δ视为建模误差，并将式（6）代入式（3）得

然后将上式写成如下形式：

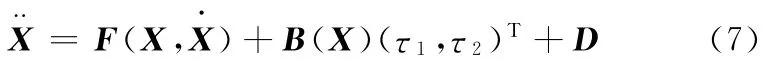
进一步写成

可见该系统是典型的欠驱动系统。

4.1.1 具有转动奇异特性的奇异位置的控制器设计

图2a～图2d所示的4种奇异位形，其驱动螺旋皆相交于一点的情形，动平台此时的转动自由度失去约束，因此式（8）中的第3个子系统是欠驱动子系统。

首先设计底层滑模函数：

式中，（xd，yd，γd）为给定的动平台参考位姿；c1、c2、c3为正常数。

然后设计2个上层滑模函数：

式中，μ1、μ2、λ1、λ2为正常数；a1、a2为常数。

式（10）和式（11）是为了保证s1与λ1s2＋s3同号，以及s2与λ2s1＋s3同号，因此，当S1，S2→0时，就能够保证s1→0与λ1s2＋s3→0，以及s2→0与λ2s1＋s3→0，从而保证s3→0，最终实现ex，ey，ez→0。

对式（8）求导得

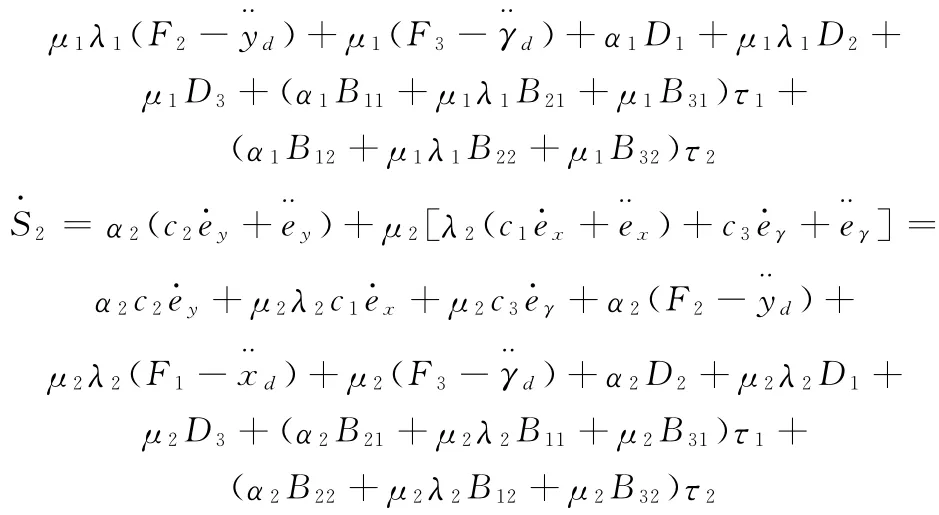
采用指数趋近律

式中，k1、k2为正常数。

因此可得虚拟控制律：

由于τ＝QTu，因此有

式中，O1、O2分别为矩阵QT的第一行和第二行。

这样可根据广义逆方法设计实际控制器：

4.1.2 具有平动奇异特性的奇异位置的控制器设计

图2e、图2f所示的2种奇异位形，驱动螺旋皆平行，表明动平台此时沿垂直于驱动螺旋方向的平动自由度失去约束，为此引入如下的线性变换：

式中，γ0为在该奇异位形下驱动螺旋相对参考系X轴的转角。

将式（14）取2阶微分，并将式（7）代入得

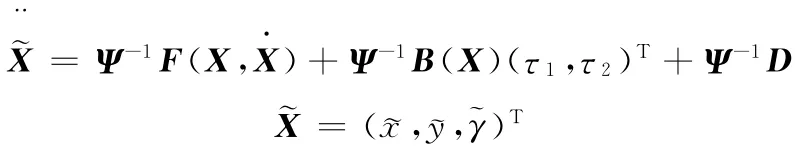
将上式进一步写成

此时，式（15）中的第一个子系统为欠驱动子系统。

设计如下的底层滑模函数：

式中，d1、d2、d3为正常数。

而两个上层滑模函数则设计为

式中，ν1、ν2、κ1、κ2、b1、b2为正常数。

因此最终可保证ex，ey，ez→0。

对式（17）求导得

采用指数趋近律

式中，ζ1、ζ2为正常数。

因此可得虚拟控制律：

同样，由式τ＝QTu根据广义逆方法设计实际控制器：

4.2 基于伪逆的滑模控制

式（3）可写成

设计滑模函数

式中，C1、C2、C3为正常数。

对式（23）求导，并由式（22）得

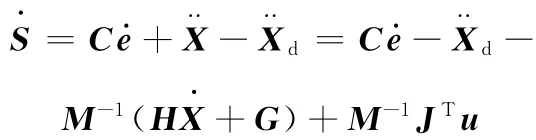
采用指数趋近律

其中，Ki、Σi（i＝1，2，3）为正常数，即可得如下控制器：

式中，（JT）＋为JT的伪逆。

5 仿真分析

并联机构的物理参数如下：mm＝5kg，Jm＝0.83kg·m2，m11＝m21＝m31＝m12＝m22＝m32＝1kg，J11＝J21＝J31＝0.3kg·m2，J12＝J22＝J32＝0.15kg·m2。 并联机构的结构参数如下：a＝0.6m，b＝0.4m，c＝1.08m，l0＝0.8m，θ0＝60°，h11＝h21＝h31＝h12＝h22＝h32＝0.3m。

首 先 给 定 初 始 位 置 （x（0），y（0），γ（0））＝（5mm，5mm，－0.1rad），目标点为如图2a所示的奇异位置（0，0，0），图3所示为利用基于分层递阶结构的滑模控制器（式（12）、式（13））得到的控制仿真结果；图4所示为利用基于伪逆的滑模控制器（式（24））得到的仿真结果。

然后再给定初始位置（x（0），y（0），γ（0））＝（－715.8mm，－232.5mm，0.96rad），目标点为图 2c 所 示 的 奇 异 位 置（－712.8mm，－216.5mm，0.98rad），图5所示为利用基于分层递阶结构的滑模控制器得到的控制仿真结果；图6所示为利用基于伪逆的滑模控制器得到的仿真结果。

图3 基于分层递阶结构的滑模控制仿真

图4 基于伪逆的滑模控制仿真

图5 基于分层递阶结构的滑模控制仿真

图6 基于伪逆的滑模控制仿真

6 结语

由图3a、图4a、图5a、图6a可见，两种控制方法都具有较快的响应速度，且能够达到较高的镇定精度；由图3b、图4b、图5b、图6b可见，基于伪逆的滑模控制方法的驱动力输入量比基于分层递阶结构的滑模控制方法的驱动力输入量要大很多，其大小实际上很难实现，因此基于分层递阶结构的滑模控制方法更有实际应用价值。

［1］Nenchev D N，Uchiyama M.Singularity－consistent Path Planning and Motion Control through Instantaneous Self－motion Singularities of Parallel－link Manipulators［J］.Journal of Robotic Systems，1997，14（1）：27－36.

［2］王玉新，李雨桐，郭瑞琴.并联机构以保持构型通过奇异位置的方法［J］.机械工程学报，2008，44（6）：125－130.

［3］Ider S K.Inverse Dynamics of Parallel Manipulators in the Presence of Drive Singularities［J］.Mechanism and Machine Theory，2005，40（1）：33－44.

［4］Jui C K K，Sun Qiao.Path Tracking of Parallel Manipulators in the Presence of Force Singularity［J］.Journal of Dynamic Systems，Measurement，and Control，2005，127（4）：550－563.

［5］Briot S，Arakelian V.Optimal Force Generation in Parallel Manipulators for Passing through the Singular Positions［J］.International Journal of Robotics Research，2008，27（8）：967－983.

［6］Kao C C，Zhan T S.Singularity Robustness of the 3RPS Parallel Manipulator by Using the Dampedrate Resolved－acceleration Control［J］.Expert Systems with Applications，2010，37（7）：5134－5144.

［7］Lo J C，Kuo Y H.Decoupled Fuzzy Sliding－mode Control［J］.IEEE Transactions on Fuzzy Systems，1998，6（3）：426－435.

［8］Lin C M，Mon Y J.Decoupling Control by Hierarchical Fuzzy Sliding－ mode Controller［J］.IEEE Transactions on Control Systems Technology，2005，13（4）：593－598.

［9］王伟，易建强，赵冬斌，等.Pendubot的一种分层滑模控制方法［J］.控制理论与应用，2005，22（3）：417－422.