基于射线管分裂方法的SAR场景快速消隐技术
2012-07-25董纯柱殷红成
董纯柱*①② 殷红成①② 王 超②
基于射线管分裂方法的SAR场景快速消隐技术
董纯柱殷红成王 超
(中国传媒大学信息工程学院 北京 100024)(电磁散射重点实验室 北京 100854)
SAR场景模型常采用非均匀三角网格描述,使得传统的基于Z-Buffer技术的消隐算法难以在保持较高的消隐精度的同时兼顾消隐效率。该文提出了一种基于射线管分裂方法的SAR场景快速消隐技术,将复杂SAR场景的消隐问题分解为两个简单过程:一是对场景三角网格在发射平面上的投影点云做2维Delaunay三角网格划分,二是基于射线管分裂方法对新生网格可见性进行判断和拓扑重构。典型飞机目标和草地上T-72坦克的消隐结果验证了该方法的准确性和高效性。
消隐算法;射线管分裂方法;Delaunay三角剖分;Z-Buffer算法;SAR场景
1 引言
对基于模板匹配的SAR图像解译而言,SAR图像中特有的透视收缩、叠掩和阴影等几何畸变特性是重要且稳定的识别特征。在低擦地角(10°~30°)条件下,高分辨率SAR图像表现出尤为明显和完整的阴影特征。地面目标SAR图像的阴影主要由地面目标的自遮挡阴影和目标-环境间的互遮挡阴影两部分组成。为准确仿真地面目标的散射特性和SAR图像中的阴影特征,不可避免地要事先确定在给定入射方向上地面目标以及环境表面的可见和不可见区域,即进行面消隐处理。
目前,常用的面消隐算法包括Z-Buffer算法、区间扫描线算法、BSP树算法、区域细分算法、射线投射算法等。其中,以Z-Buffer算法和射线投射算法的应用最为广泛。借助显卡(GPU)强大的渲染和并行计算能力,Z-Buffer算法和射线投射算法能够以秒级实现单个角度上百万量级均匀三角网格模型的消隐运算。然而,在高分辨条件下,若采用均匀三角网格对复杂目标和几百米甚至几公里的环境表面进行剖分,将产生千万甚至上亿量级的网格面元,消隐运算效率极低。为了提高SAR场景模型的消隐效率,必须大幅度减少网格面元的数量。一种可行的方法是采用非均匀三角网格(或TIN网格)对SAR场景模型进行剖分,在不明显降低模型精度的条件下产生最少数量的面元网格。因此,解决非均匀三角网格模型的快速消隐问题是实现SAR场景快速消隐的关键。
本文融合区域细分算法和射线投射算法思想,在基于kD-tree的非均匀三角网格模型GPU快速射线追踪的基础上,将非均匀三角网格模型描述的SAR场景消隐问题分解为对场景网格在发射平面上的投影点云做2维Delaunay三角剖分,以及基于射线管分裂方法对新生网格可见性进行判断和拓扑重构两个简单过程,实现了复杂场景的精确快速消隐计算。以飞机和草地上T-72坦克为例,消隐计算结果表明,本文方法能够实现复杂SAR场景实时/准实时的准确消隐,为快速获取SAR图像阴影等几何畸变特性以及目标-环境的电磁散射特性提供了高效预处理工具。
2 基于射线管分裂方法的SAR场景快速消隐
考虑到SAR场景是由非均匀三角网格描述的,基于射线管分裂方法的SAR场景快速消隐计算主要包括如下3个步骤:
(1) 发射面点云数据生成:沿入射方向对SAR场景进行自遮挡判断,并将自遮挡可见顶点投影到发射面上形成2维点云数据;
(2) 点云数据三角网格剖分:构建发射面点云数据2维凸包,并实现带凸包的Delaunay三角剖分,形成初始射线管;
(3) 网格模型可见性判断及拓扑重构:根据射线管与目标的相交情况,对射线管执行自动分裂,并根据细分射线管与场景网格的相交关系重构场景可见三角网格。
2.1 发射面点云数据生成
为加速反射面点云生成过程,沿入射方向对三角网格进行自遮挡判断,即判断三角形面元正法向与入射方向夹角的余弦
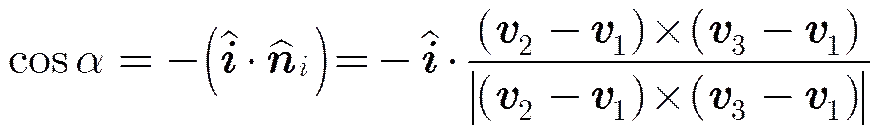

其中,为可见顶点个数,发射平面上的点由远离场景的固定点和面法向确定,如下:

式中,为场景模型的几何中心,为场景模型包围球的直径。
2.2点云数据三角网格剖分
为能够对发射面点云数据进行带凸包的2维Delaunay三角剖分,首先需要建立如图4所示的发射面局部坐标系,并将3维点云数据转换为局部坐标系下的2维点云数据,其中
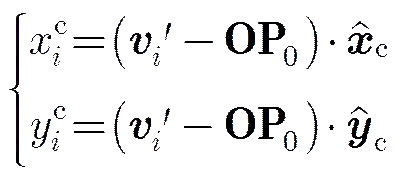
计算2维有限点云数据2维凸包(Convex Hull)的算法很多[3,4],这里不再赘述。本文采用时间复杂度为的分而治之算法[8]实现发射面点云数据2维凸包的快速构建,其中为凸包顶点个数。
三角剖分的一般要求是不存在长而薄的三角形(Slivers)。Delaunay三角剖分是一种使最小角具有最大值的方法,能够最大限度地减少狭长三角形的数量。为改进凸包边界附近的三角形的性态,在进行Delaunay三角剖分前,先求取如图4所示的2维凸包的最小包围矩形;然后按对构成包围矩形的4条边界,,和进行均匀细分,生成细分边界点,其中为细分边界点个数,且

2.3网格模型可见性判断及拓扑重构
为实现对非均匀网格描述的SAR场景模型的精确消隐处理,首先需要基于发射面点云数据Delaunay三角剖分结果生成初始射线管,在GPU上采用OptiX射线追踪引擎完成射线管顶点射线的自动射线追踪,并根据射线管顶点射线与非均匀网格的相交关系进行自动射线管分裂。本文采用的射线管自动分裂方法如图1(c)所示,阈值,,并且和越小,消隐精度越高,计算量也越大。精度和效率折中考虑,和经验值分别为和6°。对于每次分裂得到的4个细分射线管仅需追踪由原始射线管3边中点生成的3根新增射线。完成所有射线管的自动分裂计算后,即可获得全部可见射线管在网格模型面元上的第1个交点数据集。其中,为全部可见射线管个数;为可见射线管与面元模型的第1个交点个数;,和为可见射线管第1个交点索引,且。因此,重建的消隐处理后的SAR场景的可见三角网格模型由线性表表示为

(a) 1000个2维点云三角剖分结果 (b) 2维点云三角剖分效率

射线管顶点射线与非均匀网格的相交具体包括下面4种情况:
(1) 若3根射线与网格模型无交点或射线管的面积小于阈值,判定为无效射线管,直接丢弃;
(2) 若3根射线的第1个交点均位于同一面元上,判断为全部可见射线管,不再分裂;
(3) 若3根射线的第1个交点位于同一部件的不同面元上,且面元法向间夹角小于阈值,判断为全部可见射线管,不再分裂;
(4) 除上述3种情形外,都判断为部分可见射线管,需要进行分裂。
3 算例和分析
下面用飞机目标和地面上T72坦克的消隐计算实例验证本文方法的正确性、高效性和实用性。仿真硬件平台为搭载NVIDIA Quadro FX 5800 4GB GDDR3显存图形卡的HP Z800工作站。
3.1飞机目标
如图6(a)所示,飞机总体尺寸为20.09 m×13.2 m×2.33 m,其非均匀三角网格模型由423个顶点和842个三角形面元构成。图6(b)为取=43.3 mm,,沿入射,经消隐重构的由44,139个顶点和64,272个三角形面元构成的可见网格模型,消隐处理时间为1.033 s。如果将飞机按10 mm尺寸剖分(三角形面积约为),将生成由2,608,529顶点和5,217,248面元构成的均匀三角网格模型,而在同样角度下采用基于硬件的Z-Buffer算法消隐计算时间为0.841 s,消隐结果如图6(c)所示。可见,本文算法能够在达到硬件Z-Buffer算法消隐效率和精度的同时,重构更少面元数量(约为均匀剖分时的1.23%)的可见三角网格模型供后续电磁散射计算使用,并在完成SAR场景消隐处理的同时完成了场景的射线追踪,因此必将显著提高SAR场景电磁特性预估效率。
3.2 草地上T-72坦克
对SAR场景消隐重构可见三角网格模型的一个最直接的应用是高效仿真用于阴影区边界确定和姿态估计的非相干阴影模板图像。图7给出了采用本文方法快速获取的草地上T-72坦克在73°入射角0.2 m分辨率128×128像素、方位角间隔为45°的非相干阴影模板图像,其中目标、地面和阴影区域的像素亮度分别为255, 127和0。T-72场景由18, 309顶点和35, 317三角形面元构成,其单幅图像的仿真时间仅为0.2 s, 1~2 min即可完成方位角间隔1°全方位模板图集仿真。可以看出,非相干阴影图像准确重现了给定角度下目标在环境上的稳定和完整阴影特性。

(a) 非均匀网格模型
(b) 非均匀三角网格模型本文方法消隐结果

(c) 均匀三角网格模型Z-Buffer算法消隐结果
4 结论
本文提出的基于射线管分裂方法的SAR场景快速消隐技术有效融合了区域细分算法和射线投射算法思想,能够解决采用非均匀三角网格描述的SAR场景模型的精确快速消隐问题。消隐重构的可见三角网格模型能够直接用于SAR场景非相干阴影模板图像仿真,射线管分裂结果亦可直接用于SAR场景电磁散射特性计算,从而显著提高复杂目标电磁特性预估以及SAR模板图像的仿真效率。

图7 草地上T-72坦克在73°入射角、0.2 m分辨率、128像素×128像素非相干阴影图像
[1] Oliver C J, Quegan S, Ward, I A等著, 丁赤飚等译. 合成孔径雷达图像理解[M]. 电子工业出版社, 2009.
Oliver C J, Quegan S, Ward, I A,, translated by Ding Chi-biao,Synthetic Aperture Radar Image Inter- pretation[M]. Publishing House of Electronics Industry, 2009.
[2] Ross T D, Bradley J J, Hudson L J,SAR ATR: so what's the problem? An MSTAR perspective[C]. SPIE Conference on Algorithms for Synthetic Aperture Radar Imagery, Orlando, Florida, April 1999, 3721: 662–672.
[3] 和青芳. 计算机图形学原理及算法教程(Visual C++版)[M]. 清华大学出版社, 2010.
He Qing-fang. Principle and Algorithm on Computer Graphics(Visual C++ Edition)[M]. Publishing House of Tsinghua, 2010.
[4] Schneider P J and Eberly D H著, 周长发译. 计算机图形学几何工具算法详解[M]. 电子工业出版社, 2005.
Schneider P J and Eberly D H, translated by Zhou Chang-fa. Geometric Tools for Computer Graphics[M]. Publishing House of Electronics Industry, 2005.
[5] Parker S G, Bigler J, Dietrich, AOptiX: a general purpose ray tracing engine[C]. ACM Transactions on Graphics, New York, July 2010, 29(4): 1–13.
[6] Wang Pan, Liu Hua-hai, and Li Si-kun. Multi-GPU Compositeless parallel rendering algorithm[C]. 12th Inter- national Conference on Computer-Aided Design and Computer Graphics, Shenzhen university, December 2011, 66: 103–107.
[7] Zhang Chang-gong, Xi Ping, and Zhang Chao-xin. CUDA- based volume ray-casting using cubic b-spline[C]. Inter- national Conference on Virtual Reality and Visualization, Renmin University, October 2011, 10: 84–88.
[8] Shih Min, Chiu Yung-Feng, Chen Ying-Chieh.. Real-time ray tracing with CUDA[C]. Lecture Notes in Computer Science, Berlin Heidelberg, 2009, 5574: 327–337.
[9] Balciunas D A, Dulley L P, and Zuffo M K. GPU-assisted ray casting of large scenes[J]., 2006, 18(20): 95–103.
[10] Dwyer R A. A faster divide-and-conquer algorithm for constructing delaunay triangulations[J]., 1987, 2(2): 137–151.
[11] Shewchuk J R. Triangle: Engineering a 2D quality mesh generator and delaunay triangulator[J].:, 1996, 1148: 203–222.
[12] Shewchuk J R. Delaunay Refinement algorithms for triangular mesh generation[J]., 2002, 22(1–3): 21–74.
A Fast Hidden Surface Removal Approach for Complex SAR Scene Based on Adaptive Ray-tube Splitting Method
Dong Chun-zhuYin Hong-chengWang Chao
(Information Engineering School, Communication University of China, Beijing 100024, China)(National Electromagnetic Scattering Laboratory, Beijing 100854, China)
Traditional hidden surface removal algorithm based on hardware Z-Buffer technique cannot give attention to precision or efficiency at the same time when dealing with the non-uniform triangulated SAR (Synthetic Aperture Radar) scene model. A novel high-precision hidden surface removal approach using fast ray-tube splitting algorithm is proposed, where the SAR scene hidden surface removal problem is decomposed into two simple procedures,.. a Delaunay triangulator is used to generate the initial ray tubes from the projected point clouds of all incident visible vertices, then an adaptive ray-tube splitting method is adopted to carry out the complex scene shading situations and resultant visible model reconstruction. Simulation results of typical aircraft and T-72 tank show that, the new approach is feasible and effective.
Hidden surface removal algorithm; Ray-tube splitting method; Delaunay triangulation; Z-Buffer algorithm; SAR (Synthetic Aperture Radar) scene
TN957
A
2095-283X(2012)04-0436-05
10.3724/SP.J.1300.2012.20064
董纯柱(1981-),男,河南信阳人,工程师,现为中国传媒大学电磁场与微波技术专业在职博士生,主要研究兴趣为SAR图像解译和电磁散射理论计算。
殷红成(1967-),男,江西余江人,研究员,专业总师,博士生导师,主要研究兴趣为电磁散射、雷达目标特性、目标识别等。
王 超(1979-),男,陕西西安人,高工,博士,主要研究兴趣为电磁散射、雷达目标特性和数值计算等。
2012-09-11收到,2012-11-14改回;2012-12-10网络优先出版
国家部委基金资助课题
董纯柱 dongcz207@gmail.com
