一种用于多目标跟踪的增强型SMC-PHD滤波算法

吴 伟*①② 尹成友①



一种用于多目标跟踪的增强型SMC-PHD滤波算法

吴 伟尹成友

(电子工程学院 合肥 230037)(脉冲功率激光技术国家重点实验室 合肥 230037)

该文对标准型SMC-PHD滤波器作了两点改进。第一，提出基于观测值的目标个数和目标状态估计方法，该方法首先计算以观测值为行、存活粒子为列的权值矩阵，将按行计算的权值和与判决门限比较，把大于门限的观测值判决为真实观测值，并据此估算目标个数和目标状态。第二，为每个粒子分配表示存活年龄的辅助变量，以抑制强杂波环境下的目标数高估问题。仿真实验表明，在强杂波环境下，增强型SMC-PHD算法在多目标跟踪稳定性方面优于标准型SMC-PHD算法。

多目标跟踪；概率假设密度；序贯蒙特卡罗；目标出生强度

1 引言

基于传感器的观测值序列估算监视区域内出现的目标个数及其状态值是多传感器多目标跟踪领域研究的主要问题，该问题的解决面临以下困难：首先，由于目标分裂、目标消失以及新目标出现等情况随时发生，目标个数随时间变化；其次，受传感器的性能限制，虚警、漏警现象随时发生，观测值个数也随时间变化；第三，目标运动状态未知，目标与观测值之间没有一一对应关系。对此问题，近年来Mahler等人基于随机有限集理论提出了概率假设密度(Probability Hypothesis Density, PHD)滤波方法、势估计概率假设密度(Cardinality PHD)滤波方法。这些滤波方法的最大优点是无需数据关联技术便能处理复杂的多目标跟踪问题，因此得到了国内外许多学者的关注。目前已有许多具体实现算法被提出，如用于处理线性高斯情形的高斯混合PHD算法、用于处理非线性非高斯情形的标准型SMC-PHD (Sequential Monte Carlo-PHD)算法、具有航迹形成能力的PHD算法、能进一步提高状态估值精度的平滑PHD算法、能处理多机动目标跟踪的多模交互式PHD算法等各种改进型PHD算法。这些算法已在多个领域得到初步应用并呈现出良好的应用前景，如：监视雷达目标跟踪、声学目标跟踪。

在标准型SMC-PHD算法实现过程中，新生粒子生成方式和目标状态估计方法对其多目标跟踪性能影响很大。传统SMC-PHD算法通常假设新生目标只在几个固定区域起始，并以此建立新生目标模型。这种处理方法有两个弊端：(1)新目标不在新生目标模型指定的区域出现时，SMC-PHD将无法起始该目标；(2)当杂波出现在新生目标模型指定的区域时，SMC-PHD容易高估目标数，并给出错误的目标状态估值。此外，基于k-均值聚类的多目标状态提取算法在强杂波环境下性能也不是很稳定。

对于上述问题，文献[11]提出基于观测值生成新生目标模型的PHD算法，本文在此基础上提出两点改进：(1)改进目标数和状态值估计方法：计算每个观测值对所有存活粒子权值贡献的和值，并与预定门限比较，将大于门限的观测值判决为真实目标观测值，并估算目标状态值；(2)对于强杂波环境下目标数容易高估问题，本文为每个粒子引入存活年龄辅助变量，规定只有存活年龄高于某一门限值的粒子方能用于估算目标数及其状态值，以此降低错误估计出现的概率。最后的数值仿真表明，本文所提方法在目标数和状态值估计性能方面优于标准型SMC-PHD滤波器，且性能更为稳定。

2 PHD滤波器

对于多目标跟踪问题，目标状态集和观测集可分别用随机有限集和表示，其中和分别表示时刻单目标状态空间和单目标观测空间上全部有限子集的集合；是第个目标状态值，是时刻多目标数目；是传感器的第个观测值，表示时刻观测值数目。多目标跟踪问题的本质在于分析观测集合组成的-代数，最终获得多目标数目估值和目标状态估值。

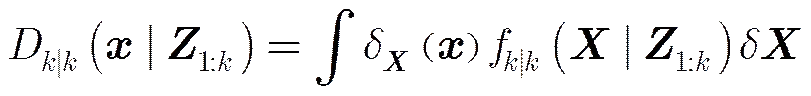
(2)

PHD滤波器包括预测和更新两个步骤，具体方程为

在未知新生目标起始位置前提条件下，标准SMC-PHD算法容易出现失跟现象；在强杂波环境下，基于目标起始位置已知的SMC-PHD算法容易出现目标数高估问题，导致状态估值错误频出。下面介绍的增强型SMC-PHD滤波算法可以有效解决上述两个问题。

3 增强型SMC-PHD滤波器

3.1 增强型SMC-PHD滤波器

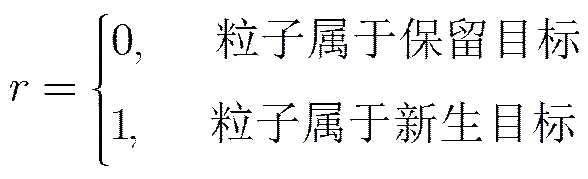
式(6)没有考虑目标裂生情况，但这不影响滤波方法的正确性，因为可将目标裂生情况当作目标新生情况处理。

考虑到前一时刻新生粒子可以在后一时刻变成存活粒子，但前一时刻的存活粒子却不能在下一时刻变成新生粒子，即，反之不成立，因此有

(9)

(11)

(13)

综合考虑式(12)、式(13)，PHD的更新方程可表示为

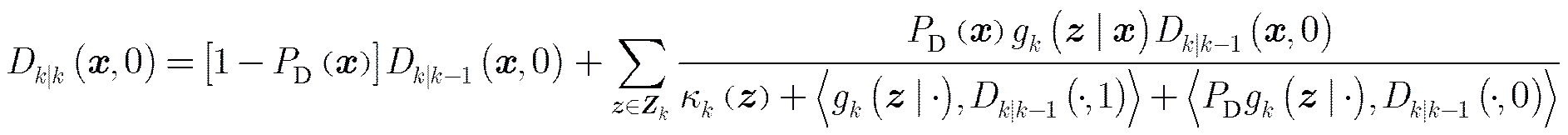
(15)

3.2 增强型SMC-PHD实现

出于算法完整性考虑，下面对增强型SMC- PHD跟踪算法的主要步骤进行总结：

步骤2新目标粒子生成步骤

步骤3更新步骤

(18)

接着更新每一个粒子的存活年龄，即

步骤4状态估值步骤

(21)

(23)

步骤5重采样步骤

4 仿真实验

4.1仿真场景设置

以2维目标跟踪场景为例，通过仿真实验证明增强型SMC-PHD滤波器对多机动目标问题的跟踪性能。假设监视区域为，监控时间，传感器采样间隔。目标在监控时间内可能作匀速或转弯运动，因此假设目标的运动模型集合由匀速模型和转弯模型组成。令时刻目标的状态矢量为=，是转弯角速度。

假设目标的状态方程为

仿真实验中多目标真实运动轨迹如图1所示：Target 1出生于第1秒，消亡于第35秒，它在1～20 s内作转弯运动，在21～35 s作匀速运动；Target 2出生于第1秒，消亡于第30秒，它在1～16 s内作匀速运动，在17～30 s作转弯运动；Target 3出生于第11秒，消亡于第42秒，它在11～30 s内作转弯运动，在31～42 s作匀速运动；Target 4出生于第21秒，消亡于第50秒，它在21～50 s作匀速运动。

图1 目标的真实运动轨迹

本文基于最优子模式分配指标(Optimal SubPattern Assignment, OSPA)来定量分析算法在目标估值精度方面的性能，关于OSPA的定义请参见文献[7]，仿真中取,。

为了验证两种滤波算法在强杂波环境下的多目标跟踪性能，本文选择虚警数，即杂波密度参数为。在新生目标粒子模型方面，假设标准SMC-PHD的新生目标出生模型为

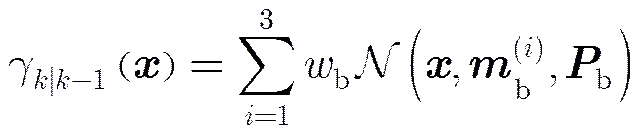
令

即只知道后3个目标的起始位置，第1个目标的起始位置未知，以此验证标准SMC-PHD滤波器对于未知起始位置目标的跟踪能力，式中。对于增强型SMC-PHD滤波器，本文通过坐标值无偏转换技术将观测值映射到状态空间，然后以位置观测值为中心，对其高斯采样获得新生目标粒子集合。在预测粒子生成方面，两种算法均先从模型库中随机选择一个运动模型，将其状态转移密度作为建议密度函数生成预测粒子集合。在目标个数和状态估计方面，前者使用k-mean方法，后者使用3.2小节所述方法。其它滤波参数设置如下：目标存活概率，传感器检测概率，新生目标数。在标准SMC-PHD滤波器中，每个目标的粒子数为500；在增强SMC-PHD滤波器中，每个新生目标和存活目标的粒子数分别为100和300，存活年龄门限，目标确认门限。

图2给出了标准SMC-PHD在强杂波环境下的多目标跟踪性能。图2(a)表明：(1)由于第1个目标的起始位置未知，标准SMC-PHD一直跟不上该目标，这表明标准SMC-PHD是以已知目标起始位置为有效滤波的前提条件的；(2)在各个目标起始位置处有大量的目标状态估值堆积在一起，出现这种现象的根本原因在于：只要有杂波出现在新生目标出生模型指定的区域附近时，标准SMC-PHD算法便会给出错误的状态估值。图2(b)表明在强杂波环境下，在大多数扫描周期里标准SMC-PHD算法明显高估了目标数，因此它的OSPA指标很差。

图2 单次实验，标准SMC-PHD算法跟踪性能

图3 单次实验，增强SMC-PHD算法跟踪性能

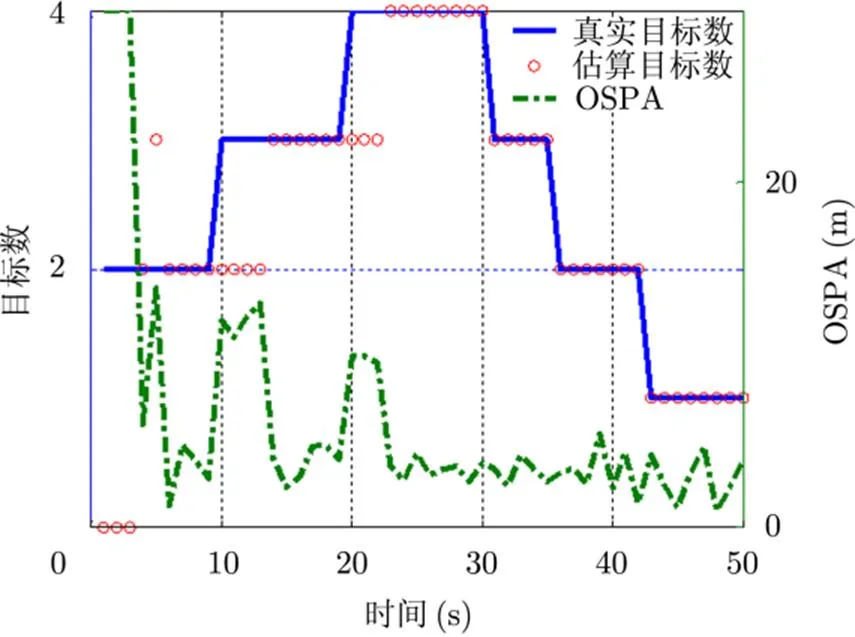
图4 单次实验，时，目标数估计和OSPA示意图

图5给出了两种滤波算法在100次蒙特卡罗仿真实验条件下关于OSPA均值的跟踪性能比较。由图易知，增强型SMC-PHD跟踪性能比较稳定；而标准SMC-PHD由于易将新生目标模型附近出现的杂波误认为真实目标，因此它的多目标跟踪性能较差。

图6给出了两种滤波算法单步计算复杂度与虚警数之间的关系图，该图是基于2.66G CPU, 2G内存、Lenovo T400计算平台，采用Matlab7.10编程计算获得的。由图易知，增强型SMC-PHD的计算复杂度与虚警数大致成指数关系，而标准SMC-PHD的计算复杂度与虚警数大致成线性关系。在虚警数小于25时，前者的计算复杂度低于后者，当虚警数大于25时，前者的计算复杂度迅速增大。

为满足算法处理的实时要求，我们可采取以下途径：(1) 提高传感器的检测性能，降低虚警数；(2)优化算法，采用C语言编程以提高执行速度；(3)引入并行计算。

图5 100次蒙特卡罗实验，两种算法在OSPA的性能比较

图6 单步执行时间与杂波数的关系示意图

5 小结

本文针对杂波环境下目标个数变化的多目标跟踪问题，提出了基于无偏转换技术的新生粒子生成方法和基于观测值的多目标个数和目标状态估计的增强型SMC-PHD算法，同时引入粒子存活年龄来抑制虚假目标的出现。仿真实验表明，增强型SMC-PHD算法在目标数估计方面性能更为稳定，在目标状态估计方面估值精度更高，在低杂波环境下计算速度也优于标准SMC-PHD算法。作者后续工作主要包括以下3个方面：(1) 如何消除因目标发生漏警所引起的目标数估计起伏问题；(2) 如何有效形成多目标航迹，克服PHD滤波器固有的困难；(3) 如何将PHD与传统多目标跟踪方法组合起来进一步提高多目标跟踪性能。

[1] Mahler R. Statistical Multisource-Multitarget Information Fusion[M]. Artech House, Norwood, 2007.

[2] Mahler R P S. Multitarget bayes filtering via first-order multitarget moments[J]., 2003, 39(4): 1152-1178.

[3] Vo B N and Ma W K. The gaussian mixture probability hypothesis density filter[J]., 2006, 54(11): 4091-4104.

[4] Vo B N, Singh S, and Doucet A. Sequential Monte Carlo methods for multitarget filtering with random finite sets[J]., 2005, 41(4): 1224-1245.

[5] Wang Yan, Meng Huadong, Zhang Hao,.. Track probability hypothesis density filter for multi-target tracking[C]. IEEE Radar Conference (RADAR), China, May 23-27, 2011: 612-615.

[6] Nadarajah N, Kirubarajan T, Lang T,.. Multitarget tracking using probability hypothesis density smoothing[J]., 2011, 47(4): 2344-2360.

[7] Mahler R P S, Ba-Tuong Vo, and Ba-Ngu Vo. Forward- backward probability hypothesis density smoothing[J]., 2012, 48(1): 707-728.

[8] Melzi M, Ouldali A, and Messaoudi Z. Multiple target tracking and classification using the unscented probability hypothesis density filter[C]. 7th International Workshop on Systems, Signal Processing and their Applications (WOSSPA), USA, May 9-11, 2011: 21-24.

[9] Hauschildt D. Gaussian mixture implementation of the cardinalized probability hypothesis density filter for superpositional sensors[C]. International Conference on Indoor Positioning and Indoor Navigation, USA, Sept. 21-23, 2011: 1-8.

[10] Plinge A, Hauschildt D, Hennecke M H,.. Multiple speaker tracking using a microphone array by combining auditory processing and a gaussian mixture cardinalized probability hypothesis density filter[C]. 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), USA, May 22-27, 2011: 2476-2479.

[11] Ristic B, Clark D, and Vo B-N. Improved SMC implementation of the PHD filter[C]. Proceedings of the 13th International Conference on Information Fusion, Edinburgh, UK, July 2010.

[12] Duan Zhansheng, Han Chongzhao, and Rong Li X. Comments on “Unbiased converted measurements for tracking”[J]., 2004, 40(4): 1374-1377.

[13] Hu Zhijian, Leung H, and Blanchette M. Statistical performance analysis of track initiation techniques[J]., 1997, 45(2): 445-456.

An Improved SMC-PHD Filter for Multiple Targets Tracking

Wu WeiYin Cheng-you

(Electronic and Engineering Institute, Hefei 230037, China)(State Key Laboratory of Pulsed Power Laser Technology,Hefei 230037, China)

Two improved contributions have been advanced for the standard Sequential Monte Carlo Probability Hypothesis Density (SMC-PHD) filter. Firstly, a novel method is advanced for the cardinality and state estimation. A weight matrix is firstly calculated by measurements and persistent particles, and the weight sum of each row is then evaluated, the measurements indexed by row will be judged as true if its weight sum is larger than a certain threshold, and the weight sum of persistent particle states will be reported as the true target states. Secondly, an assistant variable which is used to denote the persistent age for every particle is introduced, by the help of this age variable, the overrated problem of targets number in dense clutter environment can be effectively restricted. The results of numerical simulation prove that the improved SMC-PHD filter has higher tracking performance than the standard one.

Multiple target tracking; Probability Hypothesis Density (PHD); Sequential Monte Carlo (SMC); Target birth intensity

TP391

A

2095-283X(2012)04-0406-08

10.3724/SP.J.1300.2012.20094

吴 伟(1974-)，男，安徽歙县，中国科学技术大学博士学位，电子工程学院副教授，研究方向为多传感器信息融合、智能信号处理。

尹成友(1964-)，男，安徽巢湖，中国科学技术大学博士学位，电子工程学院教授，博士生导师，研究方向为多传感器信息融合、电磁场与微波技术。

2012-07-23收到，2012-12-12改回；2012-12-17网络优先出版

安徽省自然科学基金(090412067)资助课题

吴伟 wudawei@ustc.edu