基于最近邻-拓扑图的异类传感器目标关联算法

2012-07-25袁定波孟藏珍彭应宁

雷达学报 2012年4期

袁定波*① 孟藏珍①② 许稼① 彭应宁①

袁定波孟藏珍许稼彭应宁

(清华大学电子工程系北京 100084)(中国人民解放军空军预警学院武汉 430019)

针对雷达和高动态平台上的红外传感器构成的异类传感器信息融合系统中的目标关联问题，该文提出了一种基于最近邻-拓扑图的目标关联算法。该算法避免了系统误差补偿环节，有效地克服了最近邻方法对系统偏差敏感和拓扑图方法运算量大的不足，显著提高了存在系统误差条件下的关联成功率，且具有很强的稳健性。数值实验结果表明了该方法的有效性，目标关联正确率在90%以上。

数据融合；目标关联；拓扑相似性；最近邻算法；拓扑图法

1 引言

随着现代传感器技术和信息处理技术等领域的日新月异的快速发展，异类传感器之间的多源信息融合逐步体现出巨大的需求[1]。例如，目前常用的雷达和红外异类传感器组合[2]可为复杂电磁环境中目标跟踪提供解决思路。

目标关联问题是多源异类传感器信息融合的关键步骤。在对红外数据和雷达数据分别进行滤波和时空配准后，将雷达和红外数据转化到了同一个观测坐标系。由于随机噪声和传感器系统偏差的影响，不同传感器对同一个目标观测位置可发生较大的偏离。针对同类传感器的系统偏差，目前已提出了基于误差估计和补偿的方法。主要有实施质量控制法(Real Time Quality Control, RTQC)[3]、最小二乘法(Least Square, LS)[4]、极大似然法(Maximum Likelihood, ML)[5]、精确极大似然法(Exact Maximum Likelihood, EML)[6]等。但由于异类传感器信息融合系统中传感器观测数据维度不同以及时空配准引入的复杂的非线性变换等原因，难以建立方程进行系统误差估计和补偿。图1给出了时空配准后的目标的偏差示意图。可以看出偏差是时变的，且同一时刻不同目标的偏差也不一致。这为目标关联提出了很大的挑战。传统的目标关联算法如匈牙利算法[7、拍卖算法[9]、蚁群算法[10]、最近邻算法[11]等由于没有充分考虑系统误差的影响，很难取得较好的关联效果。例如，最近邻(Nearest Neighbor, NN)算法计算量小，易于工程实现。但是在系统偏差存在的情况下，其关联失配概率较大。其中，最近提出的基于多目标拓扑图的目标关联算法在系统偏差条件下实现数据关联表现出了很好的特性。但是，拓扑图方法在目标拓扑结构发生严重畸变(如翻转)的情况下失配概率大，且算法复杂度高。

图1 目标偏差曲线

本文围绕雷达-红外传感器信息融合系统，针对系统误差难以估计补偿的问题，提出了基于最近邻-拓扑图的异类传感器目标关联算法。仿真表明，新算法巧妙地避开了系统误差补偿环节，将系统误差补偿和目标关联耦合在了一起，关联成功概率在90%以上。同时，该算法具有较好的鲁棒性，可适应目标结构的较大变形，且大大降低了运算复杂度。本文结构组织如下：第2节，第3节分别简单介绍了最近邻算法和拓扑图算法的原理；第4节重点介绍最近邻-拓扑图目标关联算法；第5节给出了算法的数值仿真和结果分析；第6节对本文做了一个总结和展望。

2 最近邻算法

通常，雷达-红外目标关联中的NN关联算法

流程描述如下：

步骤1 随机选择一个雷达目标；

步骤2 从红外目标中选择一个与其最近邻的红外目标；

步骤3 将关联的雷达目标和红外目标分别从数据集中移除；

步骤4 重复步骤1至步骤3，直至对每一个雷达目标完成操作，直至结束。

通常，为了保证关联成功率，步骤1中优先选取威胁较大的目标。NN关联算法运算量小，但其关联成功率较低。在图2所示的情况下，不难看出，最近邻算法的结果是雷达目标3和红外目标4关联，关联错误。

图2 红外-雷达目标图

3 拓扑图法

基于拓扑图的目标关联算法的基本思路是利用整体拓扑结构信息进行关联。其主要流程可描述如下：

步骤2 从个雷达目标中任意选取3个构成三角形；这样的三角形构成的集合共有个元素；

步骤3 从个红外目标中任意选取3个构成三角形；这样的三角形构成的集合共有个元素；

步骤4 对于步骤2中的每一个三角形，按照式(1)中的定义，从步骤3中找出与其相似度最大的三角形并记下对应的顶点和相似度；

步骤5 综合步骤3、步骤4得出使得整体相似度最大的关联序列。

该算法有一定的局限性和缺点。式(1)所描述的相似度公式并不能判断三角形是否翻转，如图3所示。

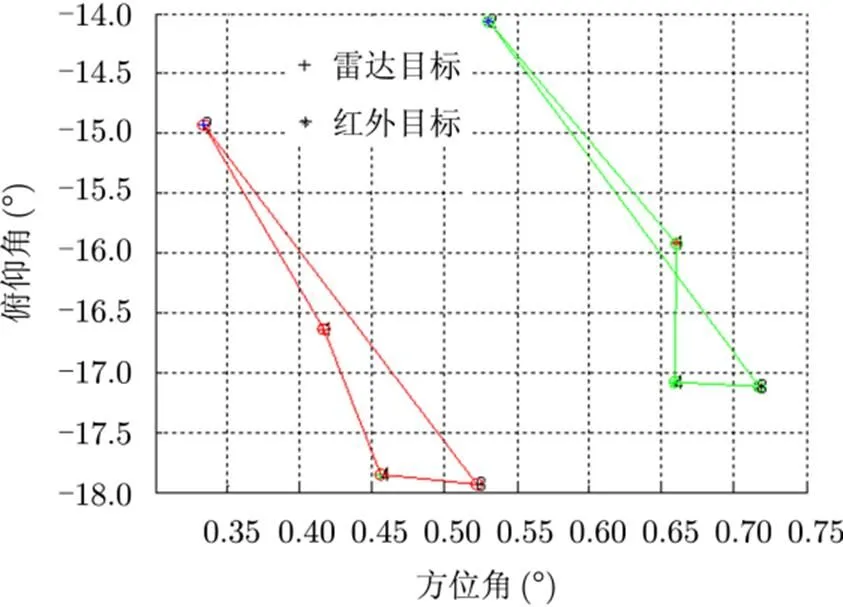
图3 红外-雷达拓扑图

实际应用中当目标相对位置翻转时，算法失效。同时，算法中步骤2至步骤4要完成个相似度计算，算法复杂度高。

4 基于最近邻-拓扑图的目标关联算法

NN关联算法运算量小但是失配概率较大，而单纯的基于拓扑图的算法在拓扑结构畸变严重的情况下失配概率较大且运算量较大。为此，基于以上两点，我们提出基于最近邻-拓扑图的目标关联算法。

4.1三角形拓扑相似度

该算法中拓扑相似度的判定依然以三角形为依托。为了判定拓扑结构是否翻转，定义如下规则：

(3)

(4)

4.2最近邻-拓扑图目标关联

基于最近邻-拓扑图的目标关联算法流程如图4所示。

图4 最近邻-拓扑图目标关联算法流程

对于雷达目标集合中的每一个目标，都减去几何形心偏差，得到新的雷达目标集合为

(7)

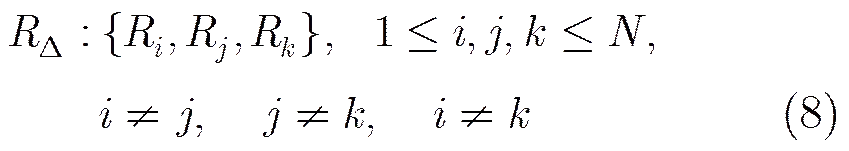
(9)

(11)

步骤6 对于步骤5中得到的相似度矩阵，利用匈牙利指派算法或者JV最短路径扩张算法，求得使整体匹配度最高的匹配序列，完成雷达目标和红外目标的匹配。

5 算法仿真及结果分析

5.1仿真数据

仿真数据设置了两个场景共计12个样本。其中场景1中设置4个红外目标，4个雷达目标，每个目标包含52点数据，方位角偏差在～之间缓变，俯仰角偏差在～之间缓变；场景2中设置4个红外目标，8个雷达目标，每个目标包含85点数据，方位角偏差在～之间缓变，俯仰角偏差在～之间缓变。

5.2 仿真结果及分析

我们分别对两个场景的6个样本进行仿真，得到两个场景的关联成功概率如表1和表2所示。

表1最近邻-拓扑图算法仿真结果(场景1)

场景-样本主目标关联成功率(%)从目标1关联成功率(%)从目标2关联成功率(%)从目标3关联成功率(%) 1-1100100100100 1-2100100100100 1-3100100100100 1-4100100100100 1-510096.1510096.15 1-610098.0810098.08

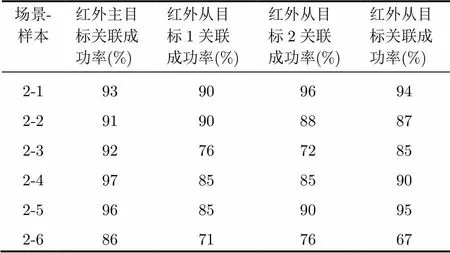
场景-样本红外主目标关联成功率(%)红外从目标1关联成功率(%)红外从目标2关联成功率(%)红外从目标关联成功率(%) 2-193909694 2-291908887 2-392767285 2-497858590 2-596859095 2-686717667

从表1，表2可以看出，本文算法将系统偏差补偿和目标关联有机地耦合在一起，受系统偏差影响较小，关联性能较高。

对于场景2的数据也利用最近邻算法进行了仿真，其结果如表3所示。通过表2、表3对比看出，由于系统偏差的影响，最近邻算法性能极差。而新算法对系统偏差不敏感，性能较好。

表3最近邻算法仿真结果(场景2)

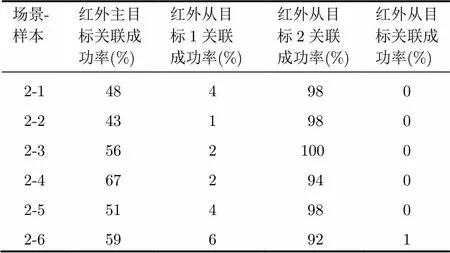
场景-样本红外主目标关联成功率(%)红外从目标1关联成功率(%)红外从目标2关联成功率(%)红外从目标关联成功率(%) 2-1484980 2-2431980 2-35621000 2-4672940 2-5514980 2-6596921

下面我们来分析雷达目标数对主目标关联成功率的影响。设定红外目标数=4时，得到主目标关联成功概率与雷达目标数的关系曲线如图5所示。从图中我们可以看出，随着雷达目标数目增多，主目标关联成功概率下降。这是由于雷达数量越大，拓扑结构越复杂，出错概率越大。同时我们可以看出，当雷达目标数目小于9时，关联成功率在95%以上；当雷达目标数小于12时，关联成功率在91%以上。

同时，由于在最近邻-拓扑图算法中涉及了邻域半径。我们分析邻域半径大小对主目标关联成功率和算法复杂度的影响得到曲线如图6所示。可以看出，邻域半径越小，算法复杂度越小，但同时会牺牲一定的算法精度。当邻域半径超过一定范围，关联成功率不再随邻域半径变换。邻域半径的大小选取反映了拓扑图的畸变程度，综合算法精度和时间的考虑，我们选取邻域半径为。

图5 雷达目标数对主目标关联成功率的影响

图6 邻域半径对算法影响

最后，在此简要分析该算法的时间复杂度。假设雷达和红外目标个数分别为和，则步骤1共需要完成2次均值运算和次减法运算；步骤2～步骤4共需要进行次拓扑相似度计算；步骤6需要对的矩阵寻优。故整体时间复杂度为量级。而拓扑图法要完成次拓扑相似度的计算，即次欧氏距离的计算，同时要完成的矩阵寻优。故其时间复杂度为量级。当取值较大时，后者算法复杂度远远大于前者。

本文算法有一定的适用范围。当传感器出现大量的虚警和漏报时，整个拓扑结构发生严重的冗余或者缺失时，基于最近邻-拓扑图的目标关联算法性能下降。

6 结束语

本文通过对异类传感器目标关联算法的深入研究，针对同一时刻系统误差对各目标大小不一且系统误差难以实时估计补偿的情况，提出了基于最近邻-拓扑图的目标关联算法。新算法巧妙地避免了系统误差对目标关联的影响，很好地解决了异类传感器目标关联成功概率较低的问题，且大大地降低了算法的复杂度。仿真实验表明新方法的目标关联成功概率在90%以上，有利于工程实现和军事应用。但同时本文算法还有待改进的地方，比如算法中邻域半径的选择如何做到自适应是下一步值得研究的地方。

[1] 郜丽鹏, 叶方, 司锡才, 等. 基于雷达、红外的数据融合算法研究[J]. 信息技术, 2005, 29(5): 8-10, 67.

Gao Li-peng, Ye Fang, Si Xi-cai,.. Study on data fusion algorithm of radar and IRI[J]., 2005, 29(5): 8-10, 67.

[2] 尹继豪, 崔炳喆. 雷达/红外数据融合的机动目标跟踪算法综述[J]. 航空兵器, 2009, (5): 39-43.

Yin Ji-hao and Cui Bing-zhe. Radar/IR data fusion algorithm for maneuvering target tracking[J]., 2009, (5): 39-43.

[3] 董云龙, 何友, 王国宏, 等. 一种改进的系统偏差估计算法[J].宇航学报, 2005, 26(6): 737-742.

Dong Yun-long, He You, Wang Guo-hong,.. One modified algorithms to estimate system errors[J]., 2005, 26(6): 737-742.

[4] 吴泽民, 任姝婕. 雷达时差和系统误差的联合估计方法[J]. 兵工学报, 2011, 32(7): 847-852.

Wu Ze-min and Ren Shu-jie. Joint estimation for time offset and radar system error[J]., 2011, 32(7): 847-852.

[5] 宋强, 何友, 熊伟, 等. 基于极大似然的单传感器误差配准算法[J]. 宇航学报, 2011, 32(8): 1826-1832.

Song Qiang, He You, Xiong Wei,.. A maximum likelihood-based single sensor bias registration algorithm[J]., 2011, 32(8): 1826-1832.

[6] 丰昌政, 薛强. 雷达组网的精确极大似然误差配准算法[J]. 兵工自动化, 2012, 31(2): 5-8.

Feng Chang-zheng and Xue Qiang. An exact maximum likelihood error registration algorithm for radar network[J]., 2012, 31(2): 5-8.

[7] 宋业新, 陈绵云, 张曙红, 等. 两类多目标广义指派问题的有效算法及其应用[J]. 华中科技大学学报(自然科学版), 2001, 29(1): 70-72.

Song Ye-xin, Chen Mian-yun, Zhang Shu-hong,.. An efficient algorithm for solving two multi-object generalized assignment problems and its application[J]., 2001, 29(1): 70-72.

[8] Gottschalk T D. Concurrent implementation of Munkres algorithm[C]. Proceedings of the Fifth Distributed Memory Computing Conference, 1990, Apr. 8-12, 1990: 52-57.

[9] 柳鹏, 高杰, 刘扬, 等. 基于拍卖算法的目标分配问题优化[J].兵工自动化, 2008, 27(9): 22-24.

Liu Peng, Gao Jie, and Liu Yang. Target distribution optimization based on auction algorithm[J]., 2008, 27(9): 22-24.

[10] 黄树采, 李为民, 李威, 等. 多传感器管理的目标分配问题蚁群算法研究[J]. 空军工程大学学报(自然科学版), 2005, 6(2): 28-31.

Huang Shu-cai, Li Wei-min, Li Wei,.. Multisensor management with ant colony algorithm for solving target assignment problem[J].(), 2005, 6(2): 28-31.

[11] 田宏伟, 敬忠良, 胡士强, 等. 基于多速率运动模型的多帧最近邻数据关联算法[J]. 上海交通大学学报, 2005, 39(3): 413-416.

Tian Hong-wei, Jing Zhong-liang, Hu Shi-qiang,.. Multiple scan nearest-neighbor data association algorithm based on multirate kinematic model[J]., 2005, 39(3): 413-416.

[12] 杨哲, 韩崇昭, 李晨, 等. 基于目标之间拓扑信息的数据关联方法[J]. 系统仿真学报, 2008, 20(9): 2357-2360.

Yang Zhe, Han Chong-zhao, Li Chen,.. Data association based on target topology[J]., 2008, 20(9): 2357-2360.

[13] Kadar I, Eadan E, and Gassner R. Comparison of robust assignment algorithms[C]. In: Kadar I, Signal Processing, Sensor Fusion, and Target Recognition VI, SPIE Conference Proceedings, Orlando, FL, USA, April 21, 1997, 3068: 240-249.

[14] 韩红, 韩崇昭, 朱洪艳, 等. 基于FCM的多传感器融合多目标跟踪的数据关联[J]. 系统仿真学报, 2004, 16(9): 2096-2099.

Han Hong, Han Chong-zhao, Zhu Hong-yan,.. Multi-sensor fusion multi-target tracking data association based on FCM[J]., 2004, 16(9): 2096-2099.

[15] 石玥, 王钺, 王树刚, 等. 基于目标参照拓扑的模糊航迹关联方法[J]. 国防科技大学学报, 2006, 28(4): 105-109.

Shi Yue, Wang Yue, Wang Shu-gang,.. Fuzzy data association based on target topology of reference[J]. Journal of National University of Defense Technology, 2006, 28(4): 105-109.

[16] Jonker R and Volgenant A. A shortest augmenting path algorithm for dense and sparse linear assignment problems[J]., 1987, 38(4): 325–340.

Target Association of Heterogeneous Sensors Based on Nearest-neighbor and Topology

Yuan Ding-boMeng Cang-zhenXu JiaPeng Ying-ning

(Department of Electronic Engineering, Tsinghua University, Beijing 100084, China)(The Chinese People’s Liberation Army Air Force Warning Institute, Wuhan 430019, China)

A new data association algorithm is proposed in this paper for heterogeneous sensors information fusion system, which consists of Radar and high-dynamic-range IR, based on joint usage of the nearest-neighbor (NN) and the topology similarity. The proposed algorithm can avoid the complicated system biases compensation based on topology information. Because the NN method is sensitive to the system bias while the existing topology-based algorithms need a large amount of computation, the proposed algorithm shows a lot of advantages, like high estimation accuracy and robustness as well as the improvement of success association rate. Finally, some numerical experiments are provided to demonstrate the effectiveness of the proposed method. And the estimation accuracy can be as high as 90%.

Data fusion; Target association; Topology similarity; Nearest-Neighbor (NN) algorithm; Topology

TN957

2095-283X(2012)04-0393-06

10.3724/SP.J.1300.2012.20083

袁定波(1990-)，男，硕士研究生，清华大学电子工程系，主要从事卫星导航等研究。 E-mail: ydb12@mails.tsinghua.edu.cn