2011年高考试题中应用开普勒定律解题赏析

王善锋

（山东省邹平县第一中学，山东 邹平 256200）

17世纪二十年代，开普勒这位身材瘦小、高度近视的科学巨人，面对模模糊糊、叠影重重的天象，聆听到了天宇的和声，揭示了约束行星运动的法则，给天庭立了法，把人们从盲目的对“天”的崇拜引向对天的探究.开普勒第三定律揭开了天文学研究的新纪元，为人类的发展立下了不朽的功勋.本文归类分析2011年全国及各省市高考试卷中应用开普勒定律解题的问题，为今后复习这部分知识提供方便.应用开普勒定律解决同一中心天体问题，简洁有效，能够使问题得以简化，因而在复习中要引起重视.

1 开普勒第三定律的基本认识

例1.（安徽卷第22题）（1）开普勒行星运动第三定律指出：行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比，即是一个对所有行星都相同的常量.将行星绕太阳的运动按圆周运动处理，请你推导出太阳系中该常量k的表达式.已知引力常量为G，太阳的质量为M太.

（2）开普勒定律不仅适用于太阳系，它对一切具有中心天体的引力系统（如地月系统）都成立.经测定月地距离为3.84×108m，月球绕地球运动的周期为2.36×106s，试计算地球的质 M地.（G＝6.67×10－11Nm2／kg2，结果保留一位有效数字）

解析：（1）因行星绕太阳作匀速圆周运动，于是轨道的半长轴a即为轨道半径r.根据万有引力定律和牛顿第二定律有

（2）在月地系统中，设月球绕地球运动的轨道半径为R，周期为T，由（2）式可得

解得 M地＝6×1024kg（M地＝5×1024kg也算对）.

点评：开普勒第三定律是由太阳系总结得到的，但对于同一中心天体形成的系统都是成立的.应用开普勒第三定律，要准确找到中心天体，从而确定常量.将运动轨道简化为圆轨道时，用轨道半径代替半长轴，而后应用开普勒第三定律，就能使问题得以解决.

2 开普勒第三定律认识同“中”卫（行）星问题

例2.（海南卷第12题）2011年4月10日，我国成功发射第8颗北斗导航卫星，建成以后北斗导航卫星系统将包含多个地球同步卫星，这有助于减少我国对GPS导航系统的依赖，GPS由运行周期为12小时的卫星群组成，设北斗星的同步卫星和GPS导航的轨道半径分别为R1和R2，向心加速度分别为a1和a2，则R1∶R2＝________.a1：a2＝________（可用根式表示）.

点评：同“中”卫星具有相同的中心天体，开普第三定律成立，将它们的轨道简化为圆轨道后，由轨道半径就可确定周期，或由周期就可确定轨道半径，从而找到问题的突破口，使问题得以解决.

3 开普勒第三定律对卫星追及问题的应用

例3.（重庆卷第21题）某行星和地球绕太阳公转的轨道均可视为圆.每过N年，该行星会运行到日地连线的延长线上，如图1所示.该行星与地球的公转半径比为

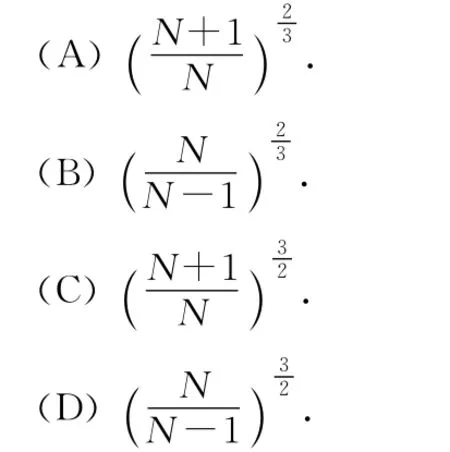
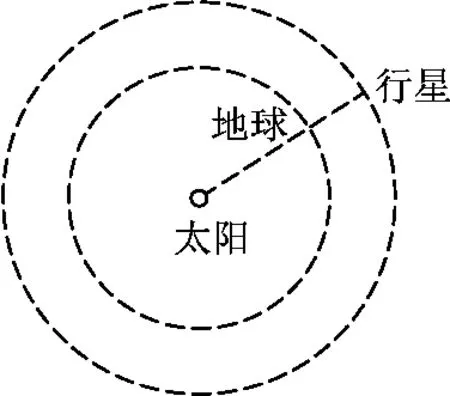
图1

解析：从行星运行到日地连线的延长线上到下次再到日地连线延长线上，地球比该行星转过的圆心角大2π，设行星的的周期为T，由此可知即，解得又地球与该行星都绕太阳转，则根据开普勒第三定律得所以选项（B）正确.

点评：天体运动是天体在万有引力的作用下做圆周运动，其角速度、线速度、加速度、周期在中心天体确定的情况下由轨道半径决定.两卫星绕同一中心天体运动，轨道半径与周期关系由开普勒第三定律找到联系.不同轨道上卫（行）星不可能直接追及相遇，但可以到达与中心天体的同一连线上，就可找到转过的圆心角关系，进而找周期关系，从而使问题找到突破口.

4 开普勒第三定律结合特殊天体特点认知问题

例4.（全国新课标第19题）卫星电话信号需要通过地球同步卫星传送.如果你与同学在地面上用卫星电话通话，则从你发出信号至对方接收到信号所需最短时间最接近于（可能用到的数据：月球绕地球运动的轨道半径约为3.8×105km，运行周期约为27天，地球半径约为6400 km，无线电信号的传播速度为3×108m／s）

（A）0.1s. （B）0.25s. （C）0.5s. （D）1s.

解析：由于同步卫星与月球都是地球的卫星，根据开普勒第三定律得即两通话的最短距离为从地球到同步卫星距离的2倍，即同步卫星高度的2倍，即同步卫星的轨道半径减去地球半径的2倍，所以有s＝2×（4.22×104－0.64×104）km＝7.16×104km，所需最短时间（B）选项对.

点评：月亮、同步卫星都是地球的卫星，它们的的周期已知，应且开普勒第三定律，可以确定它们轨道半径之间的联系，从而使问题得以突破.

5 开普勒第三定律在变轨问题中的应用

例5.（浙江卷第19题）为了探测X星球，载着登陆舱的探测飞船在该星球中心为圆心，半径为r1的圆轨道上运动，周期为T1，总质量为m1.随后登陆舱脱离飞船，变轨到离星球更近的半径为r2的圆轨道上运动，此时登陆舱的质量为m2则

（C）登陆舱在r1与r2轨道上运动时的速度大小之比为

（D）登陆舱在半径为r2轨道上做圆周运动的周期为

点评：变轨就是通过变速，改变卫星原轨道所需的向心力，从而使卫星受到的引力与向心力不等而做离心或近心运动，实现变轨.变轨过程中，由于卫星始终绕同一天体运动，开普勒第三定律是认知轨道半径与周期联系的有效关系.理解离心与近心运动的本质，撑握向心力与万有引力的关系，知道稳定运行时万有引力提供卫星做圆周运动所需的向力，就能突破问题的障碍.