运用万有引力定律处理卫星问题的通式及思考

杨小林

（深圳第二实验学校，广东 深圳 518021）

新课改《物理课程标准》将“万有引力定律”安排在必修2模块中，依据《物理课程标准》审定的不同教材关于这部分的设计各有不同，除了江苏版的设置只有两节外，其他5个版本教材都设置了3节或更多，其中人教版的达6节.从高考的考试大纲来看，以2011年广东为例，万有引力定律及其应用和环绕速度都是Ⅱ级要求（即对所列知识要理解其确切的含义及与其他知识的联系，能够进行叙述和解释，并能在实际问题的分析、综合、推理和判断等过程中运用.与课程标准中的“理解”和“应用”相当.）从历年高考来看，这部分也是必考内容.

从教学后的反馈看，多数学生认为该章比抛体运动或圆周运动难学，知识点、规律、公式、概念多，如开普勒三大定律、万有引力定律、宇宙速度、卫星的运行速度与发射速度、卫星的角速度、加速度、周期、能量、近地卫星与同步卫星，向心加速度与重力加速度的关系、卫星变轨问题、天体质量与密度的估算等等，公式、符号多，运算繁杂.其实这么多内容，都可以用一串连等式来归纳概括，公式如下：

具体分析如下：

（1）首先开普勒三大定律中考得最多的第三定律就藏在（1）式中：开普勒第三定律表达式为为行星椭圆轨道半长轴，T为行星公转周期，k为常量）由于椭圆轨道与圆十分接近，中学阶段认为a＝r，由（1）式中推出，这样我们还知道影响这个常量的因素是M（即太阳质量），这个结论也可以推广到地球及其卫星，月球及其卫星…….

（3）高中物理题中最常见的卫星运行速度、角速度、加速度、周期等均可由（1）式分别推出，对于很多选择题，我们不用定量计算，只要定性知道大小关系就可以了，所以，我们还可以定性描述上述物理量的变化规律，那就是r增大，v、ω、a减小，而周期和机械能则相反，随着r增大而增大.并且可以借助示意图来理解，答题会更快捷，如图1所示.

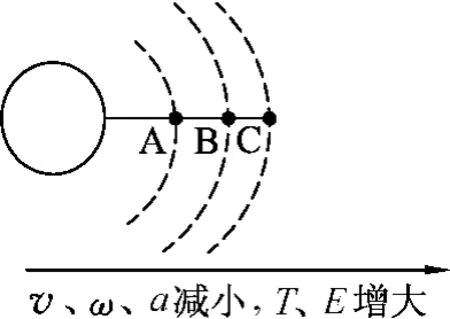
图1

（4）星球表面重力加速度g，以地球为例（以R表示地球半径）由推出gR2＝GM，此关系式被称为“黄金代换”，足见其重要性.若不在地球表面，而是在空中，则随r增大而减小.

（5）万有引力定律的应用，除了上述人造卫星外，还有估算天体质量或密度，发现未知天体等等.以估算天体质量为例，方法和思路也在（1）式中，由推出，即要估算某个天体的质量，就把它作为中心天体，去寻找它的一颗卫星的周期和轨道半径就可以了.同理也可以用（r、ω）或（r、v）求出 M，当然也可以由mg求出，若已知星球半径R及表面重力加速度g，则M

（6）关于近地卫星和同步卫星的特点，由（1）式知近地卫星，线速度就是环绕速度，和其他卫星相比速度最大.同步卫星由（1）式有由于T＝24h已确定，所以ω、h、a大小也唯一确定.

……

综上所述，（1）式是我们处理这一章问题的一个通用公式，一条线索（注意适用范围是卫星），用（1）式可以处理本章大部分的题目，请看以下两个例题.

解析：该题应用牛顿第二定律和万有引力的知识来求解，设物体所在位置高度为h，重力加速度为g′，物体在地球表面重力加速度为g，则

由（1）式得

由（2）、（3）式得

所以h＝R＝6 400km.

例2.两颗靠得很近的恒星，必须各以一定的速率绕它们连线上某一点转动，才不至于由于万有引力的作用而将它们吸引到一起.已知这两颗恒星的质量为m1、m2，相距L，求这两颗恒星的转动周期.

解析：由万有引力定律和向心力公式来求即可.m1、m2做匀速圆周运动的半径分别为R1、R2，它们的向心力是由它们之间的万有引力提供，所以

由（1）～（3）式得

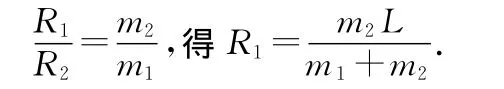
代入（1）式得

一串公式串连了本章大部分知识，当然不是说背下这串公式就学好了本章，我们如果能进行这样的归纳总结，加深理解，这个过程一定是有利于我们学习和掌握的，依据教育部考试中心考试大纲和课程标准等要求，物理科高考要考查学生5种能力：理解能力、推理能力、分析综合能力、应用数学处理物理问题能力、实验能力.当我们在理解、推导、归纳上述公式时，这些能力是应该可以得到提升的.

1 普通高中物理课程标准.北京：人民教育出版社，2003.