灰色关联决策在NSNP曲线拟合中的应用

邱 路，蒋 艳，郭晓龙

(上海理工大学 管理学院，上海 200093)

0 引言

近些年来，随着人类全基因技术发生了迅猛的发展，分析研究基因变异以及基因读取的软件和算法也越来越先进[1][2]。其中以生物统计学的发展最为明显，对于庞杂的生物数据进行汇总，并且对其进行计算研究，最后得出一些有利于科学家进行进一步研究的素材，这极大地推动了基因技术的发展。可是由于统计学的方法毕竟是有限的，在处理一些数据时，并不能真实有效地反映出这些数据的确切含义，而且有时精确度也有待于提高。

单核苷酸多态性（single nucleotide polymorphisms,SNP）为DNA序列变异的基本形式。SNP不仅可以作为遗传学标记，通过连锁或关联分析定位疾病易感基因，而且有些SNP本身就可以导致疾病，SNP对疾病的早期风险评估、早期诊断、预防和治疗等各方面均有巨大的应用价值[7]。为了探求人类的基因库中NSNPS（Novel SNPs）的变化规律，文献[1]中用了随机排序算法，将每一次排序所得的NSNP数量进行平均化，最后用STATA软件拟合出来一条曲线，拟合的确定系数98.3%。本文为了进一步提高曲线的拟合可信度，分别采用matlab和spss对于NSNP进行了4种模型的预测，4种模型中有3个确定系数都在99.8%左右。本文进一步引入灰色关联评价方法，在3个确定系数都是99.8%的曲线中再拟合出一个最优的曲线。结果表明该方法对提高拟合曲线精确度有明显的效果。

1 模型建立与问题描述

本文采取了排序算法[1]对于44个人全基因组外显子上的SNP进行了研究。本文采用R软件中随机排序算法对44个随机数进行1000次全排列，如表1。

表1 44个全基因组外显子SNP序列一次随机排列表

在此基础上，将这44个全基因组上的NSNP和合并后的NSNP进行对比，每次对比都删除重复的NSNP，最后对1000次结果求平均数。对比后的数据序列如表2所示。该表中数据包括44个基因组每次的NSNPs数，每个基因组中NSNPs的1000对比后的平均数。

表2 NSNP汇总表

表2中的平均值和基因组数作成曲线如图1:

图1 44个基因组中NSNP变化趋势图

为了对NSNP的数量进行预测，在这里我们采取了拟合曲线的方法，图2是分别用matlab和spss软件拟合的几条曲线。

图24 种模型的拟合图

从图2可以看出，几条拟合曲线都比较理想。他们的确定系数如下：虽然这四条曲线和原曲线的差别相当小，但其与原曲线的区分度依然值得提高。本文采用灰色关联评价方法以得到一条最能精确表达原曲线的函数。

2 方法提出与数据处理

灰色关联分析的基本思想是根据序列曲线的集合形状的相似程度来判断其联系是否紧密。曲线越接近，相应序列之间的关联度也就越大[8]。进行灰色关联评价的步骤如下：

首先，选取一条序列为参考序列，在这里我们采取NSNPS数这条原序列为参考序列。

X0=(X0(1),X0(2),X0(3)…X0(43),X0(44))=(3272.98,2768.01,2586.54…1489.43,1482.77)将其余四条曲线也分别变换成数字序列形式:令matlab拟合的幂曲线1：

X1=(X1(1),X1(2),X1(3)…X1(43),X1(44))=(3257.00,2824.79,2599.06,…,1504.19,1497.10)

令matlab拟合的幂曲线2：

X2=(X2(1),X2(2),X2(3)…X2(43),X2(44))=(3230.3,2819.79,2601.64,…,1495.08,1487.58)

令spss拟合的幂曲线：

X3=(X3(1),X3(2),X3(3)…X3(43),X3(44))=(3273.36,2835.83,2607353,…,1502.67,1495.54)

令spss拟合的对数曲线：

X4=X4(1),X4(2),X4(3)…X4(43),X4(44)=(3068.63,2771.09,2597.05,…,1454.13,1444.27)

其次，对于X0,X1,X2,X3,X4这5个数列进行无量纲化。在这里采取均值像法：

xi(k)d=无量纲化的5个序列如表3。

表3 无量纲化的五个序列

几种灰色关联度的公式如下:[9]

(1)灰色绝对关联公式为:

(2)灰色相对关联度公式为:

其中(n)是xi(n)初值像的始点零化像。

(3)灰综合关联度公式为：

(4)灰色相似关联度公式为：

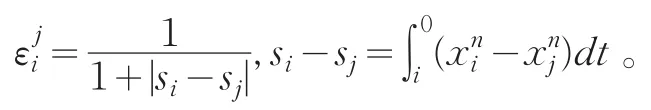
灰色系统理论建模系统3.0是一套用Visual Basic6.0开发的第一套基于Windows视窗界面的灰色系统建模软件。[9]这套软件极大地简化了数据输入中的繁琐过程，便利了灰色关联度的计算。

最后，将表3中的经过无量纲化的数据导入到灰色系统建模软件中，分别得出了4条曲线和原NSNP曲线的灰色关联度，如表4所示：

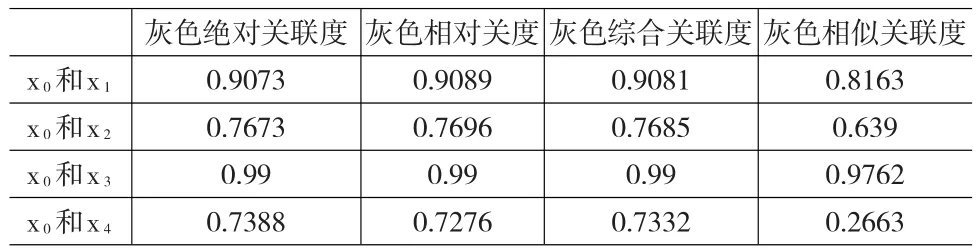
表4 4种灰色关联度对比表

由表4可见，四种灰色关联度中X3与X0都是最大的，也就是说用SPSS软件拟合的幂曲线是最优曲线，方程为：Y=3273.356X-0.207。在这四种灰色关联度中，灰色相似关联度区分度最高，这也符合了灰色相似关联度的基本思想：根据曲线几何形状来判断不同序列之间的联系是否紧密。

3 结论

为了探求44个全基因组上NSNP出现的规律，我们采取了拟合的方法，有利于对于更多数量的基因出现时对NSNP进行预测。文献[1]中采取的是STATA软件，最后的确定系数是98.3%，并没有达到最优的拟合效果。本文用matlab和SPSS拟合，并用灰色关联决策进行最后拟合比选，确定系数大于99.8%。可见采取多种软件进行拟合，并用灰色关联决策理论进行最后的拟合比选的这种决策思想，为基因变异数量的预测提供了一个很有开创性的方法。

[1]Kimberly Pelak,Kevin V,Shianna,et al.The Characterization of Twen⁃ty Sequenced Human Genomes[Z].PLoS Genet 6(9):e1001111.doi:10.1371/journal.pgen.1001111.

[2]Li H,Durbin R.Fast and Accurate Short Read Alignment with Bur⁃rows-Wheeler Transform[J].Bioinformatics,2009,25.

[3]Li-Juan,Zhang,Zhou-Jun,Li,Huo-Wang,Chenand,Jian Wen.Mini⁃mum Redundancy Gene Selection Based on Grey Relational Analysis[J].Computer Science2006,4265.

[4]崔立志,刘思峰,李致平,崔杰.一种新的灰色相似关联度模型及其应用[M].统计与决策，2010，(7）.

[5]党耀国,刘思峰.灰色斜率关联度的改进[J].中国工程科学,2004,6（3）.

[6]谢乃明,刘思峰.几类关联度的平行性和一致性[J].系统工程,2007,25(8).

[7]张小燕,胡木林,周才秀,王忠,陈沁.中风易感性与候选基因SNP位点关联研究[J].生物技术通报，2008，（增刊）.

[8]邓聚龙.灰理论基础[M].武汉:华中科技大学出版社,2002.

[9]刘思峰,党耀国,方志耕,谢乃明.灰色系统理论及应用[M].北京:科学出版社,2010.

[10]宁宣熙,刘思峰.管理预测与决策方法[M].北京:科学出版社,2008.