小样本条件下二阶分层抽样的样本最优分配研究

张金宝

（北京第二外国语学院 旅游管理学院，北京 100024）

0 引言

近年来，国内消费金融得到了较快的发展，汽车贷款、耐用消费品贷款、信用卡等越来越多的金融产品开始走进了中国居民的家庭。消费金融产品无疑将成为与普通家庭联系最密切的金融产品之一，这意味着消费金融的健康发展关乎千万家庭的切身利益。如何发挥其促进消费的积极作用，同时通过合理的政策和监管防范和化解风险，应引起政府足够的关注。

当然，关注的首要任务应是对中国居民消费金融的现状有最基本的了解。在国外，了解消费金融基本状况、获取消费金融基础数据的一个重要方法，就是在全国范围内开展以家庭为单位的消费金融调查。早在1961年，美国就开始了全国范围内的消费金融调查（Survey of consumer finance,SCF）。从1983年开始，调查开始常态化，每隔三年进行一次。加拿大、英国、塞浦路斯等国也进行了类似的调查（Alex Karagrigorou 2005）。我国的消费金融调查尚处在起步阶段，大规模的消费金融调查并未真正开始。那么，首先进行小规模的消费金融调查，积累相关的经验，为后期的大规模调查做准备不失为一个稳健可行的办法。

在此情况下，受某单位的委托我们进行了一次小规模的消费金融调查。考虑到现阶段我国的消费金融市场主要在城市，我们的消费金融调查确定以城市居民家庭为调查对象。具体地说，就是在城市的市辖区生活和居住的家庭。根据国外的经验，如何提高调查数据质量是调研的关键。从技术的环节看所采用的途径不外乎两种:一种是通过设计问卷题目，使获得的调查数据更加合理规范，降低非抽样误差。另一种则是设计合理的抽样方案尽量降低调查的抽样误差。受研究经费的限制，本次调查总的样本量为5000个家庭，拟在全国范围内调查24个城市。在制定抽样方案时，如何合理分配调查样本降低抽样误差，成为抽样设计中重点考虑的因素之一。

1 研究的准备

由于此前鲜有针对居民家庭的广泛的消费金融调查，所以关于家庭消费金融的基本状况的数据资料比较匮乏。事实上，仅仅根据现有的资料来制定抽样方案和分配样本是不现实的。但从国外的研究和国内的实践经验看，消费金融与城镇居民家庭的资产、收入、消费和储蓄等密切相关(Campbell,2006)。举个简单的例子，信用卡的授信额度、汽车贷款额度等都与居民的收入和资产成近似的正比关系。换个角度看，如果调查的样本中居民家庭的资产、收入、消费和储蓄等数据比较准确可靠，我们获得的这些家庭的消费金融数据就可能更加接近城市居民家庭消费金融的真实状况。

这给我们一定的启发：我们可以参考这些与消费金融密切相关的经济变量的信息来制定抽样方案。城市的规模和地理位置显著影响家庭的经济条件，这使得居民家庭的资产、收入、消费和储蓄等经济变量，不仅与居民家庭自身的特征变量(如人口、年龄、教育程度)有关，还与家庭所处的城市有关。因此，调查抽样拟定为二阶抽样，首先对全国的城市进行分类，在每类中先抽取城市；然后在抽中的城市里通过随机抽样最终确定调查的家庭。

研究的准备工作从城市的分类开始。对城市的分类主要考虑城市的规模、经济发展水平、储蓄水平、消费水平、消费条件等。城市规模用城市市辖区的人口来表示，经济发展水平用城市的生产总值(GDP)来表示，储蓄水平用市辖区居民的储蓄余额来表示，消费水平采用的是市辖区社会消费品零售额。根据樊纲和王小鲁（2003）的研究，对消费条件我们主要考虑了城市的交通条件、医疗条件、教育发展水平、社会保障水平、失业率等。通过聚类分析将全国的地级以上城市分成3大类。

其次，考虑到我国地区发展的不平衡，我们将全国的城市（不含港澳台地区）在地理位置上按东北、华北、华东、华南、华中、西南、西北七个大区进行划分，抽样家庭的样本数量在各个大区之间根据家庭户数按比例分配。5000个家庭样本相对于全国1亿两千万个城市家庭而言是非常小的。在样本数量有限的条件下，设计者希望每个大区至少抽取三类城市各一个。这样获得的调研数据，既能反映地理位置因素对消费金融状况的影响，也能反映不同城市类别对家庭的影响，使初步获得的调研数据尽可能多地反映家庭消费金融的基本状况，积累原始的调查经验。

具体到每个大区的样本如何在一、二、三类城市进行分配，则牵涉到本文的主题即样本最优分配问题。以华北区为例，根据总的样本分配方案，华北地区的样本数量为800个家庭。由于样本数量的限制，抽样的城市不可能太多。又由于我们希望通过抽样，对每类城市的消费金融状况都有个初步的了解，以便为下一步更大规模的消费金融调查积累经验，则每类城市至少要有一个城市入选。事实上，在华北地区我们只能在每类城市中抽取一个城市，然后在选中的城市中再按照随机抽样的原则抽取家庭。如果我们把城市的分类看做是对城市的分层，那么在每个层中我们进行的都是先抽取初级单位（城市）再抽取次级单位（家庭）的二阶抽样。

问题在于，尽管我们对城市进行了分层，但在每个层中城市的大小仍各不相同。我们面临的情况较之冯士雍、施锡铨（1995）论述的二级抽样的情况更为复杂。冯、施两人的著作讨论了总体的初级单元大小不等且只能取一个初级单元的情况下，抽样误差的估计问题。就本文的情况而言，书中讨论的情况则是发生在每个层中。本文想要解决的问题是如何在华北区三个不同类别的城市中分配800个家庭的抽样样本以便尽量降低抽样误差。因此除非特殊说明，下文讨论的“总体”均指某个大区内所有的城市居民家庭。

2 问题描述

如前所述，在缺少关于消费金融入户调查的前期资料的情况下，我们在设计抽样方案和分配样本时，更多的是考虑利用与消费金融有关的重要经济变量的间接信息。首先，使抽样方案能够对这些变量的平均水平有个比较准确地估计。为此需要描述分层情况下，由样本推测的总体均值的估计误差。

2.1 由样本推断的总体均值的误差

简单起见，我们只讨论一个变量的情形。设变量Y是要调查的家庭的经济变量（如，家庭的收入等），h代表抽样时对初级单位所划分的层，层数为L.每个层有Nh个初级单元即城市。第h个层抽取的初级单元样本数为nh=1。对于一般的分层抽样而言，由于每层之间的抽样是独立的，所以由样本推断的总体均值估计量的误差可以用公式（1）来表示：

其中，为由样本推断的总体均值，代表由样本推断的每层的均值。V代表求方差运算。Wh代表是每个层的权重，权重由每一层城市的家庭总数占整个总体家庭总数的比例来表示。式（1）表明对总体均值的估计误差是每个层的均值的估计误差的加权平均。在城市分层已经确定的条件下，根据《中国城市（镇）生活与价格年鉴2009》公布的统计数据，很容易可以算出各层的权重。因此，要描述总体均值的估计误差，关键是对每个层均值的误差作出估计就可以了。

在讨论每个层时，如果把每个层看成一个子总体的话，在这个子总体中初级单位即每个城市的大小是不同的，且在该子总体中我们只能选择一个初级单位。这个情形则与冯士雍、施锡铨（1995）论述情形颇为相似。

2.2 由每层样本推断的每层样本均值的误差

参考冯士雍、施锡铨（1995）著作，对每个层我们先规定一些标记符号：

hYij表示第h层第i个城市第j个家庭的经济变量的观测值，相应的样本记为hyij;第h层包含Nh个城市，每个层抽取的初级单位的样本数为nh。

对于h层某个固定的城市i，hMi表示该城市家庭的总数，第二阶段抽取的家庭户数为hmi，则：

对h层及该层所有的家庭而言：

hM0=，第h层样本和总体所包含的家庭的总数；

hY=第h层样本和总体所包含的家庭的重要经济变量的总和；

h第h层按家庭总户数计算的经济变量的平均值；

h第h层按城市计算的经济变量的平均值。

冯士雍、施锡铨（1995）分五种情况讨论了在不同的初级单元抽取方式下，抽样误差如何估计的问题。其中，在每层中按与初级单元（城市）的大小hMi成正比的概率抽取初级单元时（也即第h层第i城市被抽中的概率为hMi/hM0），所获得的均值估计量为无偏估计且方差最小，并且指出这种结论具有普遍意义。鉴于此，我们在每层的初级单元抽取时均采用此种方法，则每层中对家庭重要经济变量的均值的估计方差可以表示为：

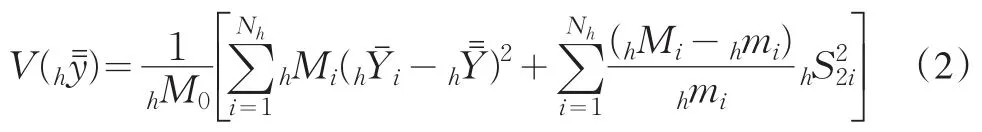
将公式（2）所表达的每层抽样的均值估计量的方差代入到公式（1），就可以得到总的抽样误差。即

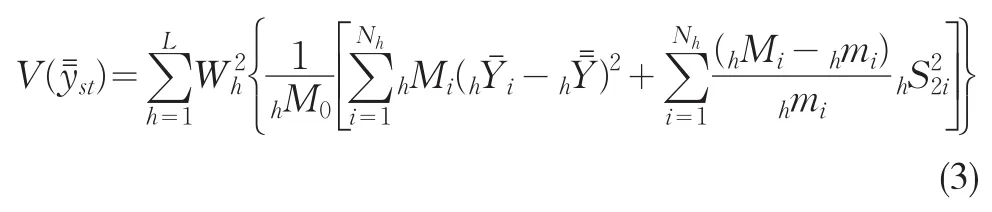
2.3 小样本条件下二阶分层抽样样本的最优分配问题

Beardwood(1959)讨论了简单的分层抽样方案中，样本量在不同的层之间如何最优分配的问题，并给出了实现最优分配时不同层的样本量之间的比例关系。但Beardwood考虑的约束条件是调查成本与各层的样本量呈正比的情况，与本文的限定样本量的约束条件有所不同。关于二阶分层抽样的成本，第一阶段的城市分层的成本主要是技术人员的数据分析发生的成本。考虑到这部分成本在总成本中占比很小，本文对其忽略不计，主要考虑第二阶段的入户调查成本。笔者在实际调研的过程中，发现调查公司的成本通常是按每户来报价，如130元/户，150元/户等。此外，大城市调查的交通成本比较低而入户成本高，小城市的入户成本低但交通成本较高。综合来看，不同类别的城市调查一户家庭的成本相差并不大，在处理时可按相等来处理。设每户的成本为c元，总的费用为tc元，则“总的调查成本一定”等价于“调查户数一定”。

假设总的样本量为mst户，在每个层分配的样本量分别为hm0（h=1,2,…L）。若使样本量在不同层之间实现最优分配，实际上是一个如何进行样本分配，使由样本推测的总体均值的估计方差最小的问题。这个思路可以用如下的最小化问题来表示：

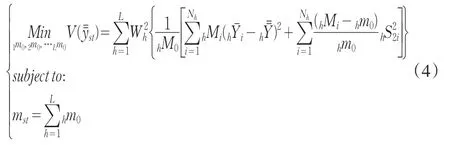
与Bearwood(1959)提出的模型相比，由于采用的是二阶分层抽样，且每层抽取的初级单位只有一个，因此本文抽样误差在形式上更加复杂。此外，尽管传统的成本约束与本文中限定样本数量的约束在本质上是一致的，但约束的数学表达仍有不同。需要说明的是，在每个层只选一个初级单元的情况下，层的样本量hm0与选中的初级单元的样本量hmi是一致的。参考Cochran W.G.(1977)《抽样技术》推荐的方法（中译本1985，张尧庭、吴辉译），在公式（4）中我们将公式（3）中的hmi用hm0代替。具体到某个城市，反映家庭之间经济变量差异的方差可以参考已有的调查资料进行估算。城市家庭的总户数，家庭经济变量的参数、可以根据统计年鉴公布的资料计算得到。这样在公式（4）中，只有样本量的分配参数为未知，求解公式（4）便可以计算出样本的最优分配。

3 研究实例

为便于读者理解本文的思路，我们仍以华北地区为例，来说明小样本条件下二阶分层抽样的样本分配问题。前期准备工作即对华北地区的城市分层已经完成，见表1。前已述及，鉴于国内城市家庭消费金融状况的资料比较匮乏，在设计抽样方案和分配样本时，我们更多地是采用与消费金融密切相关的经济变量的信息。事实上，为了稳健起见可以同时利用几个重要的变量，如家庭的收入、消费、储蓄等来测算最优样本的分配，然后综合考虑测算结果，确定最佳的分配方案。考虑到文章篇幅，本节仅以家庭消费为关键变量说明小样本条件下，在每个层只选一个初级单位时，样本量的最优分配问题。

表1 城市的分层明细

表2给出了不同城市家庭全年消费的平均值，以及每个城市总的家庭户数。其中，不同城市家庭全年消费的平均值是根据《中国城市（镇）家庭生活价格年鉴2009》中提供的城市市辖区社会消费品零售总额除以市辖区的家庭户数计算得到。

表2 华北地区的城市分级和城市家庭的平均消费水平

整个华北地区每个层城市居民家庭的平均消费水平，即可以利用表2提供的数据按照上节给出的符号定义，通过加权平均计算得到。为了给出样本的最佳分配，在公式（4）所表述的模型中，我们还需要知道不同城市家庭消费水平的方差，即目前，公开的资料鲜有披露。根据我们对北京、包头和张家口等城市居民家庭月均消费情况的调查结果，北京市城镇居民家庭的每月消费额的标准差为1414元，包头城市居民家庭月均消费额的标准差约为900元，而张家口城市居民家庭的月均消费额度的标准差为550元。考虑到公开资料较少的客观条件和简化计算，我们将这三个城市居民家庭消费额度的标准差，换算成对应的家庭年消费的标准差，作为每个层城市家庭消费额度标准差的近似值。即1S2i=1414*12=16968(i=1,2)，2S2i=900*12=10800(i=1,2,…7)，3S2i=550*12=6600(i=1,…22)。将上述已知条件代入到式（4），本节的具体问题则可以表述为：

利用Matlab软件通过编程计算可以求出上述问题的最优解。求得的结果为:1m0=394.97,2m0=251.39,3m0=153.6。对计算结果进行圆整，可得总的样本在每个层之间的最优分配为：1m0=395,2m0=251,3m0=154。需强调是，计算得出的最优分配仅仅是将居民家庭的消费作为计算样本分配的关键变量所得到的结果。在实际操作中，可以同时考虑几个与消费金融相关的重要变量进行测算。然后综合考虑测算结果作出样本分配的最佳方案。

4 结束语

根据国外的经验，消费金融调查往往涉及家庭经济活动的诸多方面，涉及家庭的资产、收入、消费、储蓄等重要的经济变量。这种内容繁多，范围广泛的调查活动往往不能一蹴而就。因此，先行的带有试验性质的调查往往成为扩大调查规模之前不可缺少的环节；反之，缺少这个环节盲目扩大调查规模则容易造成资源的浪费。这意味着，先行的试验性质的调查往往样本量较小。如何在样本量较小的情况下，通过合理分配样本量获得一个比较满意的调查结果，成为现阶段的消费金融调查必须面临的问题。

本文针对性地提出了一个解决方案。根据委托方提出的样本容量的限制，设计了二阶分层抽样的方案。在每个层中，我们只选一个初级单位进行入户调研。为了实现样本量的最优分配，我们参考冯士雍、施锡铨（1995）的著作给出了每个层的抽样误差，在此基础上描述了整个抽样方案的估计误差。再考虑样本总量限制的条件下，给出了优化样本分配的计算模型。根据模型的解设计的样本分配方案，能够在小样本的条件下尽量减少抽样误差，达到既节省成本又尽量获得准确信息的目的。

下一步可以根据本次调研获得的数据，更多地采用直接描述消费金融的变量（如家庭短期消费信贷的额度，信用卡的信用额度，住房贷款、教育贷款的参数等）来设计消费金融的抽样和样本分配方案。可以预见，抽样方案和样本分配的改进是一个逐步完善的过程。在这个过程中，只要在样本量还比较小的情况下，本文提出的方法都具有一定的适应性。当然，它也可以解决其他领域的小样本条件下二阶分层抽样的样本分配问题。

[1]Alex Karagrigorou.The Survey of Consumer Finance:Sampling and Surveying in Cyprus,[EB/OL].http://www.econ.ucy.ac.cy/～echalias/survey.html，2005.

[2]Campbell John Y.Household Finance[J].Journal of Finance,2006.

[3]樊纲，王小鲁.消费条件模型和各地区消费条件指数[J].经济研究，2004,(5).

[4]冯士雍，施锡全.抽样调查——理论、方法和实践[M].上海:上海科学技术出版社，1995.

[5]Beardwood J,Halton J H,Hammersley J M.The Shortest Path through Many Points[J].Proc,Cambridge Phil.Soc.,1959,(55).

[6]Cochran W.G.抽样技术[M].张尧庭，吴辉译.北京:中国统计出版社，1985.

[7]国家统计局城市社会经济调查司.中国城市（镇）生活与价格年鉴2009[M].北京:中国统计出版社,2009.