基于优势关系粗糙集的模糊综合评价的权重确定

吕跃进，张旭娜,韦碧鹏

（广西大学a.数学与信息科学学院；b.电气工程学院，南宁 530004）

0 引言

模糊综合评价[1]的基本思想是在确定评价因素、因子的评价等级标准和权值的基础上，运用模糊集合变换原理，以隶属度描述各因素及因子的模糊界线，构造模糊评判矩阵，通过多层复合运算，最终确定评价对象所属等级。近年来，模糊综合评价在水环境评价、财务预警、电力等方面被广泛应用[2～7]。

模糊综合评价的关键一步是权重的确定，目前权重大多由专家凭经验给出，人为干扰较为严重，可能导致评判结果不可靠。因此，很多文献采用一些客观赋权法对模糊综合评价进行改进。如文献[2]采用熵值法确定权重，文献[3]采用主成分分析法确定权重，文献[4]采用层次分析法确定权重是一种主客观结合的方法，文献[5]提出了直接根据单指标相对隶属度的模糊评价矩阵，构造层次分析法中的判断矩阵，用以确定各评价指标权重。而随着粗糙集理论[8]的广泛应用，许多文献应用粗糙集理论在模糊综合评判中确定权重，如文献[6]成功将粗糙集理论应用于确定地质因素的权重系数。但经典粗糙集面对的对象是无序的，不能很好地表达原有的偏好信息，而实际问题中的大部分指标都是有序的，例如企业发展能力综合评价中的指标净资产增长率、销售增长率等越大，企业发展能力越好。如果忽略指标的有序性就可能出现评价结果不合理。而优势关系粗糙集很好地解决了这个问题，弥补了经典粗糙集的缺陷。本文应用优势关系粗糙集提出一种度量有序决策表属性重要性的新方法，同时解决客观性和指标有序性问题。最后以企业发展能力模糊综合评价的权重确定为例，说明应用优势关系粗糙集确定权重方法是可行的。

1 优势关系粗糙集确定权重

经典粗糙集模型面对的对象是无序的，现实生活中存在的大量数据是有序的。为处理这类有序数据，Greco等人[9,10]提出了基于优势关系的粗糙集方法。本文引入对象优于程度的计量和综合优势度的概念，提出一种度量有序决策表属性重要性的新方法，然后将各属性重要性归一化处理后的结果作为每个属性的权重。

1.1 优势关系粗糙集基本概念

定义1[11]序信息系统。序信息系统是一个四元集合，I=(U,A,V,f)，其中U是论域，若U中有n个对象，则U可以表示为A是有限非空条件属性的集合，若有m个条件属性，A可以表示为V是属性的值域集，f是信息函数称≥a为相对于属性a具有优势，x≥ay表示x在a上的值大于或等于y。x≥Ay⇔∀a∈A,x≥ay。信息系统中对象的属性的值具有优势关系时，称信息系统为序信息系统。

定义2[11]优势关系。对于给定的一个序信息系统，如果B⊆A,x≥By，那么x在B上对y具有优势，记为xR≥By。

设B=B1⋃B2，其中B1是上向的属性集，B2是下向的属性集。定义对象x在属性集B上的优势集合：

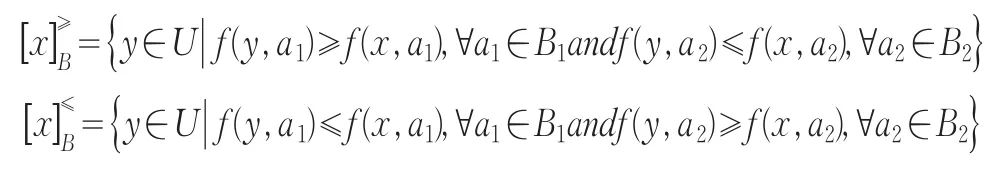
定义3[11]I=(U,A,V,f)为序信息系统且B,C⊆A。若对于任意的x∈U有，则称若 对 于 任 意 的x∈U有，则称

性质2当B⊆C时，有

定 义4[12]设I=(U,A,V,f)为序信息系统，a∈B∈A。若称a在B中是不必要的；否则称a在B中是必要的。

1.2 有序决策表的属性重要性度量及权重确定

定义5[13]对xi,xj∈U，利用粗糙集方法计算对象xi在属性集B下优于对象xj的程度为：

其中 ||∙表示集合的元素个数。显然0≤RB(xi,xi)≤1且RB(xi,xi)=1。

对象xi在属性集B下的综合优势度为[13]

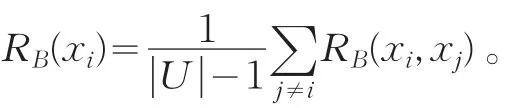
RB(xi)具有以下性质[13]：

性质40≤RB(xi)≤1；

性质5若xi＞Bxj，则RB(xi)＞RB(xj)。

RB(xi)的值越大，对象xi在属性集B下越具有优势。按照RB(xi)由大到小排序可以得到对象在属性集B下的优劣次序，记为在属性集B条件下排序得到的一组秩。利用综合优势度对对象排序直接从信息表出发，不需要其它先验信息，排序比较客观。

定义6在有序信息表I=(U,A,V,f)中，B⊆A，a∈B在B中的重要性为：

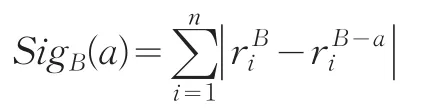
定义6表明属性a∈B在属性集B中的重要性由B中删除a后引起的秩的改变大小来衡量。

证明：

又有

证毕。

定理1设I=(U,A,V,f)为序信息系统，a∈B∈A，0≤SigB(a)，且属性a∈B在属性集B中必要的充要条件是0＜SigB(a)。

证明：0≤SigB(a)是显然的。

充分性：设属性a∈B在属性集B中不必要的，则，根据性质4，SigB(a)=0。

则命题的逆否命题：若SigB(a)≠0即0＜SigB(a)，则属性a∈B在属性集B中是必要的成立。

必要性：由于属性a∈B在属性集B中是必要的，因此由定义 4 可以知道又根据性质 2，

则至少存在一个xi∈U，使得即

可得xj≥B-{a}xi，RB-{a}(xj)≥RB-{a}(xi)。

由RB(xi)＞RB(xj)和RB-{a}(xj)≥RB-{a}(xi)可知，xi、xj排序发生变化，则根据属性重要性的定义可得0＜SigB(a)。

证毕。

最后将得到的各属性重要性按下式进行归一化处理，处理后的结果就作为每个属性的权重：

2 优势关系粗糙集确定模糊综合评价权重应用举例

在企业发展能力综合评价中，确定指标权重实际上就是确定各个反映发展能力因素的重要程度。根据得到的重要度进行归一化处理来确定权值。

以企业发展能力综合评价为例来说明如何利用优势关系粗糙集确定各个指标的权重。参与评价的企业构成评价对象集，选取的评价指标构成属性集。对象集、属性集和属性取值构成一个信息表。本文选取的反映企业发展能力的因素有销售增长率、内含增长率、可持续增长率、净资产增长率。

表1 企业发展能力B信息表

可以看出指标都是有序的，都是上向指标，即指标取值越大，表明企业的发展那能力越好。将上述信息数据离散化，分别用3、2、1表示。企业发展能力数据构成的信息表如表1所示。

其中，rij=RB(xi,xj)。

(2)同理计算出

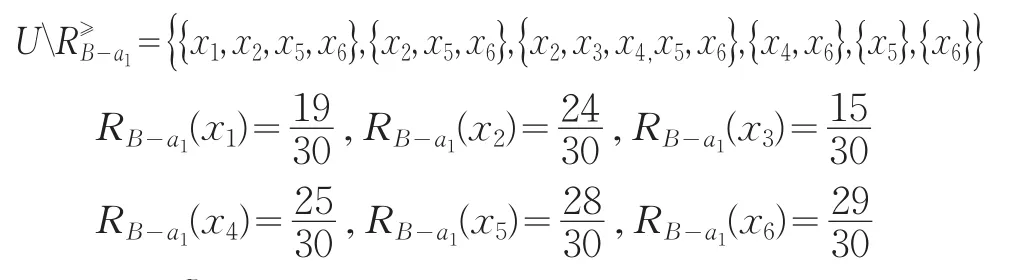
可以看出属性a2被删除后各对象的优势集合均未发生变化，序关系也不会发生变化。因此得出SigB(a2)=0。

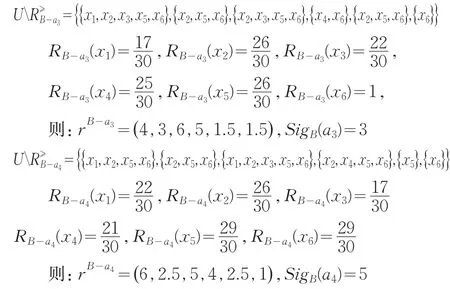
(3)根据各属性重要性进行归一化处理，处理后的结果就作为每个属性的权重：

P1=0.2,P2=0,P3=0.3,P4=0.5

3 总结

模糊综合评判时若权重系数基于专家经验给出，则因其主观性过强可能给出错误的结果。本文提出的基于优势关系粗糙集确定权重方法完全是由原始数据决定的，是一种完全客观的赋权方法，且可以解决指标的有序性问题。在实际应用这种方法时要考虑数据的代表性和离散化方法等问题。

[1]李士勇.工程模糊数学[M].哈尔滨:哈尔滨工业大学出版社,2004.

[2]梁冬青.基于熵权的模糊综合评价方法在火电厂选址的应用[J].煤,2010,19(1).

[3]田海龙,李岩,高维春.基于因子分析法原理的水环境模糊评价模型[J].吉林化工学院学报,2009,26(2).

[4]陈凯华,张孝远.模糊综合评价模型的改进及应用[J].甘肃科学学报,2009,18(3).

[5]金菊良,魏一鸣,丁晶.基于改进层次分析法的模糊综合评价模型[J].水力学报,2004,(3).

[6]石骁,赵庆飞.基于粗糙集理论的模糊综合评判权值确定[J].西南石油学院学报,2001,23(3).

[7]黄杰刚,路杨,位华,许云.基于模糊综合评价的上市公司财务危机预警[J].管理科学文摘,2004,(3).

[8]Pawlak Z.Rough Sets:Theoretical Aspects of Reasoning about Data[M].Bostont:Kluwer Academic Publishers,1991.

[9]Greco S,Matarazzo B,Slowingski R.Rough Approximation of a Prefer⁃ence Relation by Dominance Relation[J].European Journal of Opera⁃tion Research,1999,(117).

[10]Greco S,Matarazzo B,Slowingski R.A New Rough Set Approach to Multicriteria and Multiattribute Classificatioin[C].Polkowsik L,Skow⁃ron A.Rough Sets and Current Trends in Computing（RSCTC’98）,Lecture Notes in Artificial Intelligence.Berlin:Springer-Verlag,1998.

[11]张文修,梁怡,吴伟志.信息系统与知识发现[M].北京:科学出版社,2003.

[12]桂现才.序信息系统属性约简的一种启发式算法[J].计算机工程与应用,2008,44(27).

[13]张文修,仇国芳.基于粗糙集的不确定决策[M].北京:清华大学出版社,2005.