质押存货长期价格风险测度模型的构建

何 娟,蒋祥林,王 建,陈 磊

（1.西南交通大学交通运输与物流学院，成都，610041；2.复旦大学金融研究院，上海，200433；3.华夏银行成都地区信用风险管理部，成都 610000）

0 引言

近年来，面对巨大的市场需求，以及业内日益激烈的竞争，国内外金融机构纷纷试水供应链金融这一业务。尽管供应链金融市场潜力巨大，但是对供应链金融风险问题的担忧一直制约着动产质押融资业务的繁荣。作为主要业务模式之一的存货质押贷款通过使用存货作为质押物来降低和规避贷款的信用风险。在进行质押贷款的评定过程中，对质押资产的估价是为了评判在未来贷款时期内质押品的价值是否能保持对贷款的担保能力，而这就需要准确测度未来一段时期的质物价格波动风险，为业务实施中质押贷款比率的确定做提供定量的决策依据。因此，对质押存货的长期风险水平的准确测度和预测，对于防范存货质押业务的交易风险以及保证供应链金融市场的健康平稳运行，都具有非常重要的理论和现实意义。

与质押存货价格风险的已有研究相比，本文的价值主要体现在：（1）鉴于质押存货同金融资产价格收益波动相似的特点即表现出尖峰后尾特征和波动集聚性，引入学生t分布和广义误差分布，建立厚尾分布下的VaR-GARCH族模型；（2）预测未来波动率时，样本外预测更具实用性（White,H,2000）[1]，文中以样本外预测方法预测未来质押内多风险窗口下的长期波动率，进而得到厚尾分布下长期VaR的解析式；（3）为确保研究的可靠性和稳健性，基于失效率方法建立碰撞序列函数，并引入正态分布下的Risk-Mertrics模型，对厚尾分布下的VaR-GARCH族模型进行后验比较分析，保证VaR的预测精度。进而为银行实践中动态合理度量风险提供决策依据。

1 长期价格风险测度模型构建

1.1 VaR-GARCH族模型构建

综合考虑影响质物价格收益序列的尖峰厚尾特征及波动集聚性等多方面因素后，建立厚尾分布下的VaR-GARCH族模型计算质物的长期价格风险。

1.1.1 质押存货收益率的计算

假定质押存货在t日的市场价格为Pt，t-1日的市场价格为Pt-1，日收益率采用对数收益率为：

1.1.2 质押存货波动率的计算

质押存货的波动率即是指质押存货收益率的标准差σ。为了精准的刻画收益率的异方差性即波动率的集聚性，引入GARCH模型，而前人研究发现，GARCH(1,1)模型可以描述绝大多数的金融序列的时变方差，故在此使用GARCH(1,1)进行质物资产收益率的波动率进行预测。建立条件均值方程和条件方差方程如下：

其中，Rt表示t交易日的对数收益率；μt为对数收益率的条件均值。Tsay在其专著中亦指出绝大多数的金融资产的对数收益率序列是不相关或低相关的，这也成为波动率研究的一个基本思想[2]。因此文中，先验假设条件均值为零，也近似可以接受。εt≡σtzt为随机扰动项，又称残差项，其中zt为新生变量（Innovation）；σ2t为第t交易日的条件方差；α0为常数项，α1为ARCH项的参数估计值，β1为GARCH 项的参数估计值，而且α0＞0，α1＞0，β1＞0。

1.1.3 新生项zt的建模

在GARCH模型建模过程中，往往将新生项zt默认设置为正态分布，而实际上往往呈现尖峰厚尾性。为此，Bollerslev(1987)首次提出了学生t分布来刻画收益率的尖峰厚尾特征[3]，其概率密度分布为：

其中，n为自由度，当n→∞时，t分布趋近正态分布。

而Nelson(1991)发现广义误差分布（Generalized Error Distribution，GED）刻画收益率序列尖峰厚尾特征具有更为优良的性质[4]，其分布密度函数为：

本文拟以Fugate的就业能力指标作为依据和参考，以职业认同感、社会资本、个体适应力、人力资本为评价标准，在此基础上，细分为自信心、市场意识、技能、健康、交际范围、人际交往的主动性等十五个指标对新生代农民工就业能力进行探究和评价。运用AHP法分别计算出每个一级指标和二级指标的权重，据此了解和分析不同的指标变量对新生代农民工就业能力是否存在影响、影响的程度，以及影响的规律性，在此基础上进而探讨在不同方面、不同条件下如何逐步提高新生代农民工就业能力的建议。

实证分析中，将根据两种分布对尖峰厚尾性质的刻画能力，进行选取。

1.1.4 质押存货VaR的计算

鉴于质押钢材价格的波动性，以及风险发现到风险处置的时间差，实践中，商业银行在开展存货质押业务时，须选择合适的风险窗口T去测度风险，实时动态评估其市场风险（价格风险），以便在质押期内能根据风险变化动态测度风险。

如前所述，存货质押业务中VaR的计算实质上是长期风险预测，而非局限于未来某一天短期风险的预测。这也是近年来金融机构新开展的诸如供应链金融等新兴业务的共同特点，同时这也契合了巴塞尔协议Ⅱ以及最新的巴塞尔协议Ⅲ对银行向监管机构报告大于两个周甚至一年的VaR监管要求。然而国内外的研究多以2周以内的短期风险为主，关于长期风险预测的研究则相对缺乏。现有的长期风险的研究均是基于时间平方根法则即然而时间平方根法则有着严格的限定条件，即要求对数收益率序列服从均值为零的独立正态分布，这与大部分金融资产的对数收益率序列展现出的尖峰厚尾特征不符。在用于股票、期货等短期风险预测时，得到的VaR只是一个近似值，而对于存货质押业务等长周期预测，若采用近似值将产生较大误差。因此，为了得到更为精确的VaR，Dowd et al(2004),Pengfei Sun[5,6]对时间平方根法则进行了修正：

其中，pt为资产的初始价值（为分析方便，全文均以单位资产的价格作为初始价值）为置信水平α下的左侧分位数，μt，σt分别为两个估计变量t时收益序列的条件均值和条件波动率。虽然这种方法较初始时间平方根法则有所改进，但条件波动率的预测依然采用了时间平方根法则，这虽然避免预测每日条件波动率的繁琐，却同样对存货质押业务长期波动率的预测带来误差。因此如何基于考虑了波动率时变性的GARCH(1,1)模型进行厚尾分布下的长期波动率预测成为关键。Andersen,Bollerslev et al(2006)给出了不考虑自相关时，厚尾分布下GARCH(1,1)模型下的长期波动率的预测[7]：

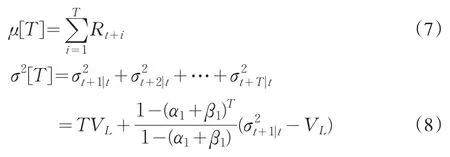
其中：

VL=为无条件方差。

据此，得到厚尾分布下的长期风险VaR：

作为衡量风险窗口T内银行潜在损失值的VaR，需关注风险窗口（持有期）T值和置信水平α两个参数的选择。其中，风险窗口T往往被银行等金融机构视为清算期，这与资产的流动性有关，由于商业银行多为流动性强且交易十分迅速的货币资产，其往往以日为期限计算VaR。而对于质物，理论上T的设定则要结合供应链金融市场实际流动性状况、样本规模以及质物资产头寸的调整等因素予以调整；实务中，银行则可以根据自身风险偏好，除重点考察质物本身的流动性即变现能力等质物自身特点外，还要结合供应链金融交易对手资信状况、贷款企业的偿债能力、盈利水平等财务指标以及供应链运营状况进行综合考量。而对于置信水平α的选择则根据银监会对商业银行市场风险的计量要求，取为99%。

1.2 回测模型构建

为了检验厚尾分布下的VaR-GARCH(1,1)模型的有效性，必须检验模型得出的风险值VaR对质押存货实际损失的覆盖程度。在回顾测试中应用范围最广是Kupiec[8]提出的失效率检验法，失效率也就是检测样本内VaR被超越的次数，理想的情况下，失效率应该接近于1-α，失效率过大或者过小均说明VaR模型不能准确刻画实际风险。

基于这种思想，在预测质押存货的价格风险时，以预测的存货价格被实际价格击穿的次数来检验失效率，建立如下碰撞序列：

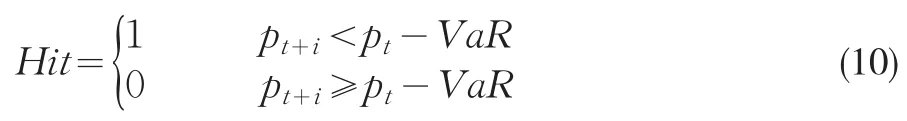
其中，初始价格减去持有内的风险值即为预测价格pf。定义N为风险窗口内的总样本数，f为预测价格被实际价格击穿的次数，则在统计意义上应为1-α。

2 数值实验

2.1 样本数据选取与统计特征描述

2.1.1 样本数据的选取

本文样本取自于在我国房地产等基建行业需求较为旺盛的螺纹钢，根据西本新干线和上海期货交易所提供的上海螺纹钢（φ16HRB335）的价格波动数据。本文以2005/9/05～2008/12/31四年的数据（共计868个样本点）作为确定参数的估计样本，2009/1/01～2009/12/31的数据（共计261个样本点）作为检验样本，对其进行模拟质押，质押合同起始日为2009年1月1日，质押期设为质押最长期限12个月。结合银行操作实务，风险窗口可分设为1个周、半个月、1个月、2个月、3个月、4个月、5个月、6个月、7个月、8个月、9个月、10个月、11个月和12个月。

2.1.2 样本内价格对数日收益率统计特征描述

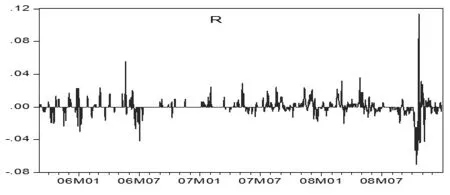
图1 上海螺纹钢对数日收益率波动状况

如图1所示，上海螺纹钢的对数日收益率序列的波动呈现明显的集聚效应，即大的波动后往往跟随着大的波动，小的波动后跟随着小的波动。这说明序列R的随机扰动项可能存在ARCH效应。

表1 上海螺纹钢对数收益序列的基本特征描述

表2 对数日收益率序列R的ADF单位根检验结果

表3 上海螺纹钢对数日收益率序列的残差的ARCH效应检验结果

表1中，偏度大于0，且峰度远大于3，J-B检测值显著，说明上海螺纹钢日对数收益率序列呈显著的尖峰厚尾分布，且D-W值接近于2，可以近似不存在自相关；表2中通过ADF（单位根检验），收益率序列是稳定分布；而表3通过拉格朗日乘数检验，表明对数收益率序列存在显著地ARCH效应，可以运用GARCH模型对波动率建模。

2.2 参数估计及数值实验结果比较

表4 t分布下GARCH(1,1)模型的估计结果

表5 GED分布下GARCH(1,1)模型的估计结果

对比表4、表5发现，t分布下的常数项α0不显著，而GED分布下各项系数均显著，因此使用GED分布刻画收益率分布的尖峰厚尾性，AIC/SC合理，残差序列已不存在ARCH效应，将表5中各参变量值代入式（2）和（3），得到描述螺纹钢时变波动率的GARCH(1,1)模型。

由式（12)可得α1+β1=0.86＜1，故满足GARCH(1,1)模型的平稳条件，可以用来预测条件方差,随机误差项的条件方差可以收敛到无条件方差：=2.3724E-05。根据Eviews程序求得GED分布在参数v为0.853,置信水平为99%时的左侧分位数为-2.87。

根据式（7）、（8）、（9）分别计算出质押期为12个月（2009/1/01～2009/12/31）模拟质押期内多风险窗口下的长期风险VaR（见表6），为进一步得到预测价格pf，建立碰撞序列函数，进行模型回测比较做好准备。

表6 12个月的模拟质押期多风险窗口的实验结果

3 模型回测比较

根据失效率检验法则以及碰撞序列函数（10）对模拟质押期内各风险窗口的风险值进行回测，并将实践中广为应用的基于独立正态分布假设Risk Metrics模型（时间平方根法则）引入，与厚尾分布下的VaR-GARCH(1,1)模型对比分析，主要结果如表7，表8。

综合分析可以发现，金融实务界主流的Risk Metrics模型虽然在大部分的风险窗口内，能正确估计长期风险值，但在3个月和4个月的风险窗口内，预测价格被实际价格分别击穿10次和15次，致使失效率远远超出了99%置信水平所接受的例外情况；与之相比较，厚尾分布下的VaR-GARCH(1,1)模型在3个月和4个月的风险窗口内出现了8次和3次例外，尤其在4个月的风险窗口内失效率远低于Risk Metrics模型。这表明VaR-GARCH(1,1)模型度量长期风险在统计意义上更为有效，预测精度更高。

4 主要结论

表7 基于Risk Metrics12个月的模拟质押期多风险窗口的实验结果

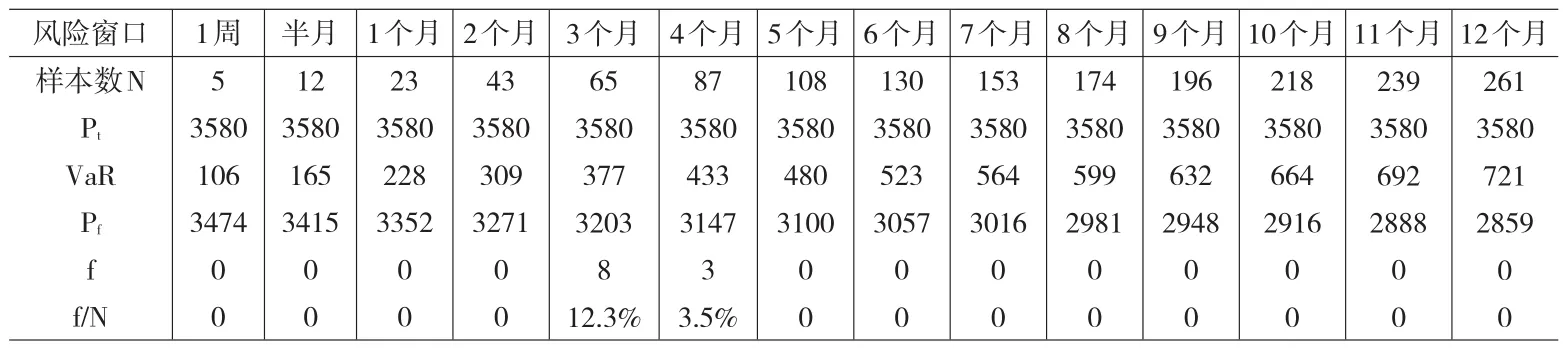
表8 GED分布下的VaR-GARCH(1,1)模型下12个月的模拟质押期多风险窗口的实验结果

针对存货质押业务流动性不活跃引起的银行风险持有期较长，本文以上海螺纹钢为算例，建立了能刻画日收益率尖峰厚尾特征及波动集聚性的VaR-GARCH(1,1)模型，得到了厚尾分布下长期风险VaR解析式，测度质押期内多风险窗口风险值。实证结果表明：螺纹钢展现出显著的尖峰厚尾特征及波动集聚性，而且广义误差分布较学生t分布更好的刻画了收益率的厚尾性质，最后经失效率检验，厚尾分布下的GARCH(1,1)模型相较实践中应用广泛的Risk Metrics风险预测模型具有更高的预测精度，为商业银行提供一种动态价格风险管理框架。进一步，该研究结果可以在供应链采购合约管理、价格管理以及质押率设定等方面扩展使用。

需要指出的是，为实践操作简单，论文采用GARCH模型进行厚尾分布下的长期波动率预测，重点研究了条件波动率，忽略了质物对数收益率可能存在的自相关性。这或许正是3个月的风险窗口内失效率较大的原因。如何考虑收益的自相关性的同时进行长期波动率预测，以提高长期VaR预测的精度，为银行防范风险、提高收益提供定量决策依据，是需继续研究的问题。

[1]White,H.A Reality Check for Data Snooping[J].Econo⁃metrica,2000,68(2).

[2]Ruey S.Tsay.Analysis of Fi⁃nancial Time Series[M].New York:John Wiley&Sons,Inc,2005.

[3]Bollerslev,T.A Conditionally Heteroskedastic Time Series Nodel for Speculative Prices and Rates of Return[J].Review of Economics and Statistics,1987,(69).

[4]Nelson,D.B.Conditional Heteroskedasticity in Asset Returns:A New Approach[J].Econometrica,1991,(59).

[5]Dowd,K.,Blake,D.,Cairns,A.Long-Term Value at Risk[J].The Journal of Risk Finance,Winter/Spring,2004.

[6]Pengfei Sun.The Estimation of Long-Term Risk from Data about Short-Term Risk[D].University Bielefeld,2009.

[7]Andersen,T.G.,Bollerslev,T.,Christoffersen,P.F.,Diebold,F.X.Vol⁃atility and Correlation Forecasting[A].In:Elliott,G.,Granger,C.W.J.,Timmermann,A.(Eds.)[Z].Handbook of Economic Forecasting.North Holland Press,Amsterdam,2006.

[8]Kupiec,P.Techniques for Verifying the Accuracy of Risk Measure⁃ment Models[J].Journal of Derivatives,1995,32(2).