基于熵—Shapely的样本差异赋权方法

席雪红

（郑州航空工业管理学院，郑州 450015）

0 引言

我国地域广阔、各地资源禀赋层次不齐，不同的资源对差异地区的发展约束不尽相同。在这样的背景下，对我国各区域发展水平作出一个合理并符合实际的评价对我国顺利实现“东部率先发展、中部崛起和西部大开发”的共同推进具有重要意义。常规的评价主要侧重于指标体系的构建，如李答民（2008）从结构、变量关系、制度、可持续性和增长力等5个维度，采用了价格指数等15个评价指数和指标连乘法对31个地区的经济发展水平进行了定量评价；王永洁等（2007）则使用了主成分分析方法将评价体系设为4个维度，对宁夏下属各市进行了发展水平评价。上述研究的指标体系构建具有一定的合理性和实践性，但应关注的是这些文献中或多或少都在避免一个几乎所有评价研究都不能忽视的问题：指标权重。类似的研究中，如汪波等（2004）直接采取AHP层次分析法对指标体系赋权;杨霞(2011)在构建指标体系的基础上，采用了熵权和灰色GM组合的方法的进行赋权，对我国区域农业发展水平进行评价。本文提出了一种基于熵权基础上修正的shapely二次权重方法，对以往评价过程中赋权的一次性操作提出修正，并使用该方法进行实例分析，以期对相应研究有帮助。

1 熵—Shapely二次权重修正方法

信息熵的概念源自于物理学分析，对于任何一种信息其自身都具有一定的膨胀性，具体到经济学领域，对于n个样本的多指标（如m个）评价，会有一个矩阵：

矩阵中xij表示第i个对象中第j个指标的值，形成了n×m矩阵，表示存在n行（评价对象个数）、m行（评价指标个数），那么对于指标j而言，其存在正负向指标区别，如j(1)指标在评价中越大越好，如经济增速、资产周转率等，而有一些指标在评价中以越小为好，如废水排放率、未通过率等，那么对于负向指标必须进行转化，一般可以采用数据倒数法和最大值减法进行处理，为了方便叙述和操作相对简单，这里不再具体说明，即假设（1）中所有指标为正向指标；由于不同指标存在量纲不同，需要进行归一化处理，具体公式为：

即在特定指标下不同样本的数值除以该列总和，如果zij越大，表示在j指标下，i单位的信息熵越大。计算熵权值的公式为：

将（3）式转化为最终的权重公式，权重为：

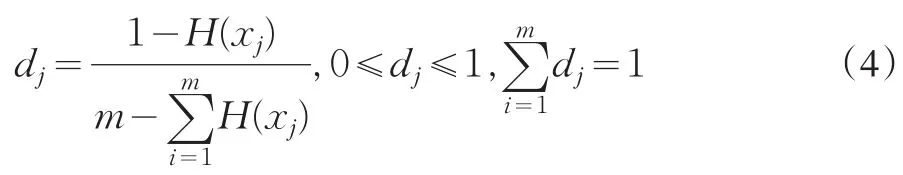
这种通过指标体系内部信息熵的挖掘得到的赋权方法就称熵赋权，克服了以往评价赋权中AHP的主观性。但是，不得忽视的一个问题是：一个具体的指标虽然原则上来说应该有dj的权重，这种权重效力的发挥依赖于指标数值的大小，比如在经济发展水平评价过程中，一些欠发达省份的某一指标数值相对较小，那么这个指标的意义就不是非常显著，故笔者提出了一种基于shapely的熵权修正方法。具体步骤为：

（1）设立临界判别值。对于指标j中的样本数值xij，其占最优值代表了在i样本在j指标固有权重上的实现度。

（2）对原有权重修正。对于每个i而言，j指标原有权重为上述计算出的dj，这里认为j指标对不同研究对象的权重是不一样的，得到的调整贡献度为：gij=γij∗dj。

（3）Shapely权重计算。这里认为对于集合G=[gi1,gi2,…gim]的任意子集G*⊆G（共2m个），具体计算公式为：

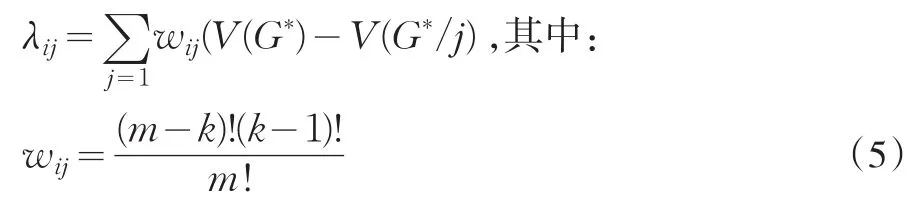
其中V(G*)——G*组合的权重发挥总效力，V(G*/j)——G*组合的权重发挥总效力，k为G*组合中指标的数量。可以发现经过处理后λij≠dj,由于每个样本在独立指标下的权重发挥效度不同，故最后计算出的最终权重也不相同。值得注意的是：这种赋权方法弱化了劣势指标的权重，而强化了强势指标的作用，这种方法具有一定的说服力：在很多区域评价中，一些地方在资源禀赋、劳动力人数方面有优势，而在技术创新和基础设施建设上存在不足，如果按照全国整体的唯一权重（资源禀赋、劳动力人数等优势指标的权重较低）对其进行评判，必然会造成评价的不公平出现。

2 实例分析

2.1 初始熵权计算

存在评价指标集X=[x1,x2,x3]和样本集Y=[y1,y2,…y10]，具体数据结构用（1）式的矩阵形式表示：

表1 熵权计算结果

可以发现三个评价指标的量纲完全不同，分别是[0,10]、[0,100]和[0,1]数据区间类型。假设所有指标均为正向指标，故不需要再进行同向化处理，可以根据实际对经济情形对号入座，比如对应为企业利润额（万元）、销售额（万元）和各项指标综合达标率。按照（2）～（4）式进行各指标初始权重。其中调节系数k=1/ln10=0.4343，计算出的熵权值H(xj)和最终权重dj如表1所示，表示三个指标中x1重要性最强，达到了0.550，其次是x3为0.261，x2的权重最小为0.187。

2.2 差异样本下的Shapley权重调整

（1）计算单个样本的权重实现度和调整贡献度。计算结果如表2所示，在2-1中，通过每列数据除以该列数据中最大值得到，可以看出在指标1上样本8完全实现，同理指标2和指标3上样本2和样本3完全实现，这样体现了不同样本在不同指标上的相对优势；表2-2通过每列数据与所代表的指标初始权重（表1中第三行）相乘得到的结果。

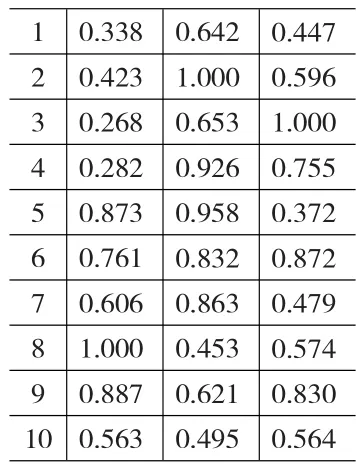
表2 -1 权重实现度

表2 -2 调整贡献度

表3 样本1的指标权重计算

（2）shaply权重修正。以样本1为例，其构成的指标集为I=[1,2,3]（这里为了方面计算和序数，故省略了x符号），设置门限值为这个门限值的意思是某个集合指标贡献度超过了全要素权重的一半值，这个评价指标体系的信度比较可靠。下面以样本1中三个指标权重计算为例，门限值为：（0.186+0.120+0.117）/2=0.2115，若V(s)＞0.2115，则由P(s)=1,否则等于0。

那么有映射关系：V（1）=0.186，V（1,2）=0.306，V（1,3）=0.303，V（1,2,3）=0.423。表3中表示包含指标1在内所有[1,2,3]的子集，第二行k为集合中元素个数，V(k)是包含集合得到的利益，V(k-1)是去除指标1后剩下元素集合的收益，然后根据门限值得到P值，具体见表3。表最后三行是需要的数据，运用（5）计算出指标1的权重是1/3；那么同样得到其他两个指标权重也分别为1/3。这样，按照上述运算，同样可以得到其他样本的各指标权重。

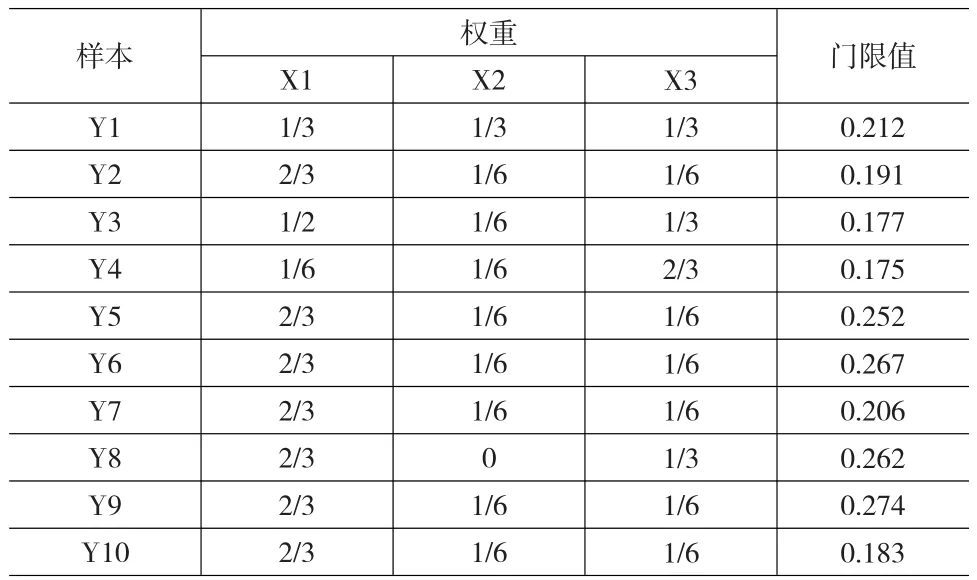
表4 经过shaply法修正后的样本差异权重

表4中显示了每个分析样本在三个指标上的权重分布，从纵列上看，Y2,y5～y10共六个对象的指标1权重为2/3，比初始权重0.55增加了0.167，而Y1，Y3，Y4在不同程度上权重呈现缩小趋势，指标2权重上除样本1外均呈现缩小趋势，如对象9该指标权重为0，但整体上缩小趋势不大，因为1/6与0.187差距较小。指标3上指标呈现出普遍权重缩小现象，因为初始权重为1/4，除了1,3,4,8样本该指标权重增大外，其他六个全部变小。上述研究结论体现了不同指标在对不同样本进行评价时的权重变化思想。

3.3 评价结论

由（6）中的矩阵数据和表4的权重数值，根据（7）可得到评价得分。

表5 熵—shapely评价得分及排序

表5中给出了基于熵—shapely的权重修正评价结果，表示X8＞ X9＞ X5＞X6＞ X4＞X7＞ X3＞X10＞ X2＞ X1,为了进行对比，这里采用熵权法得到初始权重再次进行评价，结论如表6，可以发现两种方法的评价结果存在很大差异，前四名的总体位置没有发生变化，X8和X9、X5和X6排名颠倒，X2经权重修正后由第六名变为第9名，X3和X10的排名也互相颠倒了一次。可以认为：shapely权重修正不会引起大的排名变动，即不改变原有数据分析内在结构和机理，而只是在排名比较相近的分析样本排序上进行具体修正，如上面分析的“相近样本名字倒换”特征。这样基于样本差异的权重波动分析方法，对经济管理乃至其他各类社会评级研究至关重要。

表6 初始权重评价得分及排序

4 结论

本文在对评价研究过程中赋权方法相关研究文献的基础上，提出了一种基于熵—shapely的样本差异指标赋权方法，这种方法改变了以往研究过程中对于不同样本进行评价时采取一致指标权重的传统做法，根据实例研究发现这种方法评价的结果不会在数据结构上有别于其他评价方法，但其存在的微调作用不可小视，希望有关学者能够在此基础上做进一步研究，对解决评价过程中的赋权难题作贡献。

[1]李答民.区域经济发展评价指标体系与评价方法[J].西安财经学院学报，2008,（5）.

[2]王永洁，刘小鹏，赵亚峰.区域经济发展的综合评价及优化—以宁夏为例[J].宁夏大学学报，2007,（1）.

[3]汪波，方丽.区域经济发展的协调度评价实证分析[J].中国地质大学学报（社会科学版），2004,（6）.

[4]杨霞.我国农业发展水平的GM-熵赋权组合评价[J].统计与决策，2011,（19）.