基于HHT的胃电信号处理

续大伟，史学涛

1.第四军医大学 生物医学工程系，陕西 西安 710032；

2.陕西省肿瘤医院 设备科，

陕西 西安 710061

基于HHT的胃电信号处理

续大伟1,2，史学涛1

1.第四军医大学 生物医学工程系，陕西 西安 710032；

2.陕西省肿瘤医院 设备科，

陕西 西安 710061

本文采用HHT（Hilbert-Huang Transformation，HHT）时间序列分析方法，处理从人体采集到的胃电信号，通过经验模态分解（EMD）技术将一非线性、非稳态过程的原始胃电序列分解为一组内在模态函数（IMF），然后对每一个IMF进行Hilbert变换，这样得到信号的瞬时频率，然后选择与胃电成分相关的频率成分，即2～4 cpm之间的IMF进行重构提取胃电信号，这是一种更具自适应性的、新型的、基于模态分解的时间序列数据处理方法，可以有效去掉叠加在胃电信号中的呼吸和血流等干扰信号，使胃电图（EGG）在临床诊断中更具有实际意义。

胃电图仪；胃电图； Hilbert-Huang变换；经验模态分解

0 前言

胃电图（Electrogastrogram， EGG）是指由胃电图仪从人体上腹部体表记录到的胃电信号。它可以有效地反映胃电活动的状况，具有一定的临床诊断价值[1]。由于它是来源于脏器性信号源，极易受噪声干扰，主要表现在来自呼吸、测量过程中人体的轻微运动、小肠电活动、心电活动等方面的干扰。因此，信噪比较低，波形不经过处理难以直接利用。在非平稳信号的时频变换理论中，小波变换具有完备性、正交性、局部化、自适应等特点，其基本运算包括伸缩和平移，从而形成信号的多尺度分析，并能同时有效地分析信号的时间和频率特性。尽管小波变换能够分析非平稳信号，但还是存在许多不足之处[2]。Hilbert_Huang 变换（HHT）是由Huang等人 1998 年提出的一种具有高时频分辨能力的信号分析方法。其核心包括 2 个部分 :经验模型分解（Empirical Mode Decomposition，EMD）和 Hilbert谱分析。

1 胃电图的组成成分及其特征[3-9]

人的胃和心脏一样，也存在着电活动。EGG主要是由胃电控制活动引起的一种自动慢波，其频率正好对应胃收缩的最大功率。慢波是一直存在的，它源自沿胃大弯的胃体的近 1/3 结和远 2/3 结的区域，它具有重复变化的特性，并向幽门传播，其速度和幅值逐渐增加。慢波的频率约为3 次 /min，患有胃功能性疾病的人表现为节律失调。一般认为，慢波只完成电起搏功能。一些研究表明，慢波与窦平滑肌的低幅值收缩也有一定的关系，当出现阶段收缩时，胃电响应活动（ERA）引起峰值（SPIKES），在 EGG 中表现为信号幅度的增加。另外，由于EGG来源于器官性信号源，极易受噪声干扰，主要干扰源有：呼吸噪声、电极与皮肤摩擦噪声、市电干扰噪声和来自其他器官的电活动。虽然在仪器记录EGG时，可由记录仪器滤除部分噪声，但EGG 主要是低频成分，能量微弱，质量差，必须经过有力的信号分析工具处理，否则很难直接用于临床诊断。

主频和主功率是 EGG 的主要参数。主频是指 EGG 取得最大功率处的频率，它能比较精确地反映胃慢波的频率。正常人通常为 3 次 /min，若不在这个频段，则是胃慢波异常。主频处的功率称为主功率，反映了胃慢波的幅度和奇点，功率的变化能提供胃收缩强度的运动信息。

1.1 经验模态分解（EMD）

该分解过程基于一个假设，即采集的数据是由许多基本的内在模态函数（IMF）叠加而成，它们是线性或者非线性，并且具有相同数目的极值点与过0点，即要求在横坐标上下对称分布。

不同时间尺度的各种模态根据其特征尺度进行分离，对任意给定时间段，可能同时存在许多运动模态，它们互相叠加得到原始获得的复杂信号。分离之后每种模态是相互独立的，在连续的过0点之间不存在其他的极值点。

IMF 所要满足的判断条件 ：① 整组数据极值点和过 0点的数目相同或者最多相差 1 个 ；② 局部极大值包络线和局部极小值包络线的平均值为0，也就是说信号的上下包络线对称于时间轴。

在实际信号的处理过程中，完全满足第二个条件是不现实的，所以只要二者的平均值小于一个预先确定的小量即可，根据定义，可以按照如下方法分解函数，设时间序列为X(t)。

（1）找出X(t) 的所有极大值点和极小值点，并将其用三次样条函数拟合为原始数据序列的上下包络线。上下包络线的均值为平均包络线m1，将原序列减去m1得到一个新序列h1，即 ：

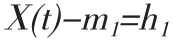
经过这次分离，突起的值成为新的局部极大值和局部极小值。此过程有两个目的：消除载波和让波形更加对称。

（2）一般来讲，h1不一定是一个平稳序列，为此需要对它重复上述过程，将h1看作原始数据，找到其包络的中心线m1继续分解，则有：

重复以上过程，经过k次，直到满足以上两个限定条件，结束分解，使得h1k成为第一个 IMF 项，即 ：

C1为从该数据分离出的第一个 IMF 分量，它代表原始数据序列中最高频成分。原始信号X(t) 与C1的差值为剩余信号r1：

由于r1包含了较长周期的组份，可将其视为原始数据并重复以上的过程获得C2，其新的差值为 ：

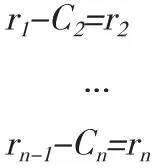
当rn为单调序列或者相对原始信号幅度极小可忽略不计时，认为完成提取信号内在模态的过程，此时代表原始数据序列的均值或者趋势。综合以上方程，最后获得：

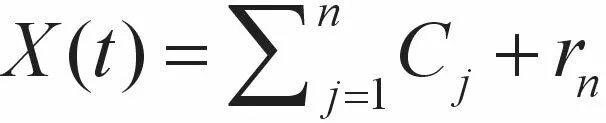
从此方程可知，原始信号可以表示为n个内在模态函数和 1 个剩余信号rn之和，rn是常数或是一组单调数据，所有的 IMF 分量经过逆向叠加，最后可以还原回原始数据X(t)。

1.2 Hilbert变换

设X(t) 为一时间序列，Y(t) 是它的 Hilbert变换，即 ：

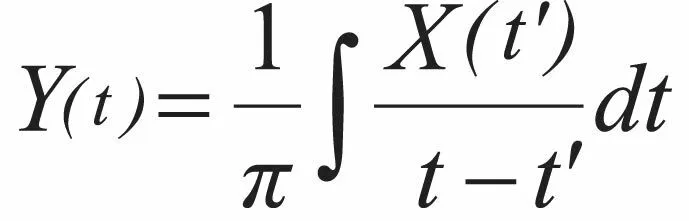
X(t)和Y(t)形成一复数，可以得到X(t)对应的解析信号Z(t) ：

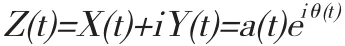
将信号的瞬时幅值 a(t)、瞬时相位 θ(t) 表示如下 :

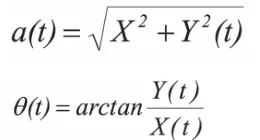
式中w(t)为t时刻的瞬时频率。

2 实验结果

对人体实测的胃电信号，应用EMD方法进行分解，得到各个时间尺度下的内在模态分量，选择与胃动力信号频率相关的模分量进行重构，可以滤除各种干扰，提取出胃动力信息。

实测采集到的一段原始胃动力信息数据（图 1），虽然3 次 /min 的慢波节律可以大概分辨出来，但是信号中含有明显的较高频率的心电、呼吸干扰以及低频的基线漂移等。

图1 原始采集胃电信号

对图1中的信号进行经验模态分解，得到8个内在模态分量和1个趋势分量，8个内在模态分量分别表示一定的周期特性。对 EMD 分解的 8 个 IMF 分量（图 2），主要是对应于胃电信号中低频成分及干扰；剩余分量Rn表示的是测试时间内的信号变化趋势。

对分解后的各个 IMF 分量进行 Hilbert变换，求出每个内在模态分量的瞬时频率，然后选择与胃动力相关的频率分量 IMF3、IMF4、IMF5、IMF6 进行重构，重构后的胃电慢波信号，见图3。

图2 EMD分解后的8个IMF分量

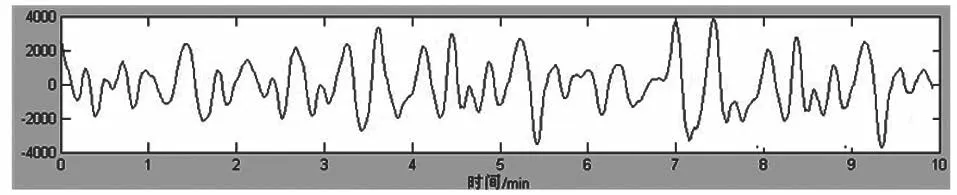
图3 重构后的胃电信号

原始采集的信号功率谱（图 4），含有心电，呼吸以及低频等干扰成分。由经过EMD 方法提取出的胃电信号功率谱（图5）可以看出，处理后的信号消除了基线漂移的影响，并且有效地抑制了各种干扰，其频率成分主要分布在 2～4 次 /min。

图4 原始信号功率谱

图5 重构后信号功率谱

3 结束语

本文采用经验模态分解方法，自适应地分解胃电信号，再对实际信号的内在模分量进行重构，可以有效抑制实际采集信号中的基线漂移、心电、呼吸等干扰，可很好地提取胃电信号，为进一步分析胃电信号的各种特性及其临床应用奠定了基础。

经 EMD 分解变换得到的 IMF 序列是直接从原始数据中分离出来的，实现无需确定分解次数，不受人为因素影响。因此，IMF 序列能更好反映原始数据固有的物理特性，其分解是客观的，内在的和自适应的。实验结果表明，它是一种行之有效的方法，为分析胃电信号提供了一种新的强有力的工具。

[1] 蔡建华,吴敏金.基于小波变换的EGG信号处理[J].华东师范大学学报,2000,(3):43-47.

[2] TSE P,YANG W X,TAM H Y.Machine fault diagnosis through an effective exact wavelet analysis [J].Journal of Sound and Vibration,2004,277(5):1005-1024.

[3] 杨振江,王承德.胃电信号的检测与处理[J].电子科技,1995,(12):55-57. [4] 刘海龙.生物医学信号处理[M].北京:化学工业出版社,2006.

[5] 张德丰.Matlab 数字信号处理与应用[M].北京:清华大学出版社,2010.

[6] Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for non-linear and non-stationary time series analysis [J].Proceedings of the Royal Society of London Series A-Machematical Physical and Engineering Sciences,1998,454:903-995.

[7] PENG z K,TSE p w,CHUA F L.An improved Hilbert-Huang transform and its application in vibration signal analysis[J]. Journal of Sound and Vibration,2005,186(2):187-205.

[8] 刘理,任惠茹,李刚.胃电图的记录、分析及其应用[J].生物医学工程学杂志,2003,20(3):567-570.

[9] Holly Moore.matlab实用教程[M].2版.北京:电子工业出版社, 2010.

Gastric Electrical Signal Processing Based on Hilbert-Huang Transformation

XU Da-wei1,2, SHI Xue-tao1
1. Biomedical Engineering Department, Fourth Military Medical University, Xi’an Shaanxi 710032, China; 2. Equipment Department, Shaanxi Provincial Tumour Hospital, Xi’an Shaanxi 710061, China

In this paper, the Hilbert-Huang Transformation (HHT) method is adopted to deal with the gastric electric signal collected from patient bodies. Nonlinear and non-stationary original gastric electric signal series can be decomposed by using the empirical mode decomposition method(EMD) into a number of intrinsic mode function(IMF)components. Under the Hilbert transformation process, instantaneous frequency are effectively extracted. Selected the related frequency, such as 2～4cpm, then reconstructed the signal. This is a new and applicable time series analysis method based on mode decomposition. This method can accomplish the extraction of gastric electric signal and remove the disturbances such as blood flow and breathing. HHT is an easy and effective method to do EGG analysis in clinical diagnosis.

electrogastrogram system; electrogastrogram; Hibert-Huang transformation; empirical mode decomposition

R319；R573

A

10.3969/j.issn.1674-1633.2012.07.011

1674-1633(2012)07-0044-03

2012-02-20

本文作者：续大伟，在读硕士研究生，临床医学工程师，陕西省医疗器械协会理事。

史学涛 ，副教授，硕士研究生导师。

作者邮箱：dawei5228@sohu.com