典型阵列快速MUSIC算法研究

张兴良* 王可人 樊甫华



典型阵列快速MUSIC算法研究

张兴良王可人 樊甫华

(电子工程学院信息系 合肥 230037)

由于MUSIC(MUltiple SIgnal Classification)算法需要大量的乘法运算和三角函数求值，导致其实时处理能力较弱。为此，该文首先对均匀线阵和均匀圆阵的阵列结构进行分析，提取导向矢量的一些性质。然后，利用Hermite矩阵的性质对复数乘法进行分解，再组建两个实值向量以减少乘法运算次数。最后，利用导向矢量的性质提出一种基于查表的新算法。新算法既没有三角函数求值运算，又不需要大量的存储空间。仿真实验结果表明新算法在没有改变MUSIC算法谱估计的效果的前提下，将MUSIC算法的运算速率提高了50倍以上。因此，新算法具有广阔的应用前景。

典型阵列；导向矢量；查表法；快速MUSIC(MUltiple SIgnal Classification)算法

1 引言

传统的空间信号谱分析法是傅里叶变换法，由于阵列尺寸有限，该方法的分辨率受到瑞利限的约束。以多重信号分类 (MUltiple SIgnal Classification, MUSIC)算法为代表的子空间类处理方法，即所谓超分辨空间谱估计算法，突破了瑞利限的限制，实现了谱估计理论的重大飞跃。近年来，这类算法广泛应用在通信、雷达和航天等诸多领域，其优点早已得到实践证明。

遗憾的是，超分辨空间谱估计算法需要大量的乘法和三角函数求值，因此其计算耗时难以满足工程需要。在圆阵、方阵等2维阵列中，该问题表现得更加突出。实际上，巨大的计算量已成为超分辨空间谱估计技术完全走向实用化的主要瓶颈之一。

快速空间谱估计算法一直是国内外学者研究的热点，目前主要的研究思路有3种。第1种是寻找新的计算量小的空间谱估计算法，这类算法的估计性能往往不如MUSIC算法，并且一般只适合均匀线阵，如ESPRIT算法和Root-MUSIC算法。第2种是对现有的空间谱估计算法进行改进，这类算法实际上是在精度和计算量之间进行折中选择。如文献[7]改用信号子空间实现基于FFT的快速MUSIC算法，但降低了谱估计的精度；文献[8]只降低特征分解的计算量，却没有降低谱峰搜索的计算量，改进效果不明显。第3种是根据算法的运算流程和特点，合理设计和配置硬件，这类方法的效果也是有限的，而且往往是以牺牲硬件成本为代价，如多路并行谱峰搜索法。以上研究成果在一定程度上提高了超分辨空间谱估计算法的计算速度，但是仍然不能满足要求越来越高的现代实时处理要求。

文献[7]分析了MUSIC算法计算量大的主要原因：搜索范围大和谱函数复杂，也就是说，谱峰搜索占MUSIC算法计算量的绝大部分。谱峰搜索的计算量主要包括乘法和三角函数求值，计算机完成这两种运算的过程都比较复杂，耗时严重。为此，文献[12]利用查表法降低了圆阵列MUSIC算法的乘法和三角函数求值次数。但该文献提出的直接查表法对存储量需求大；提出的间接查表法依然保留大量的三角函数求值运算，效果有限。

本文重点研究快速MUSIC算法。在减少乘法运算次数的基础上，利用查表法避免三角函数求值运算；针对查表法需要较大存储量的情况，利用导向矢量的性质对查表法进行了改进。相较于文献[12]的查表法，本文提出的算法既没有三角函数求值运算，又降低了对存储量的需求，且本文的研究范围包括均匀线阵和均匀圆阵两种阵列。本文第2节深入研究阵列的内在特征，获得导向矢量的内在性质；第3节去除蕴含在MUSIC算法中的冗余乘法；第4节介绍查表法；第5节对查表法进行了仿真分析，仿真试验结果令人满意；第6节总结全文。

2 典型阵列分析

虽然MUSIC算法对阵列结构没有特殊要求，但为简单起见，工程中都选用具有典型结构的阵列。本文研究的典型阵列包括均匀线阵和均匀圆阵，均匀线阵是典型的1维阵列，均匀圆阵是典型的2维阵列，它们的阵列结构模型分别如图1和图2所示。需要说明的是，本文建立的模型是以下列假设为前提的：

(1) 入射信号是远场的，且是窄带的；

(2) 相邻阵元间距小于信号载波波长的一半；

(3) 接收噪声是平稳高斯白噪声，入射信号互不相关，各阵元接收噪声相互独立，信号与噪声也相互独立。

2.1 均匀线阵

其中

图1 均匀线阵结构图

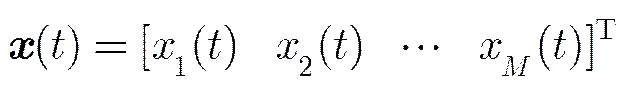
(3)

(4)

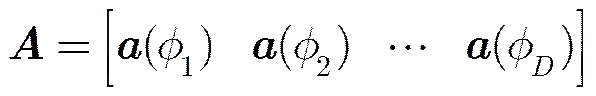
(6)

性质1均匀线阵导向矢量具有共轭对称性，即

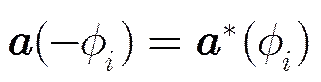
证明

(8)

2.2 均匀圆阵

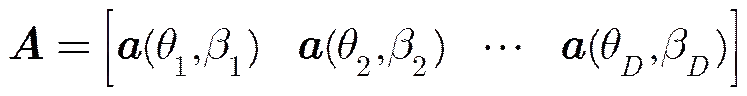
(10)

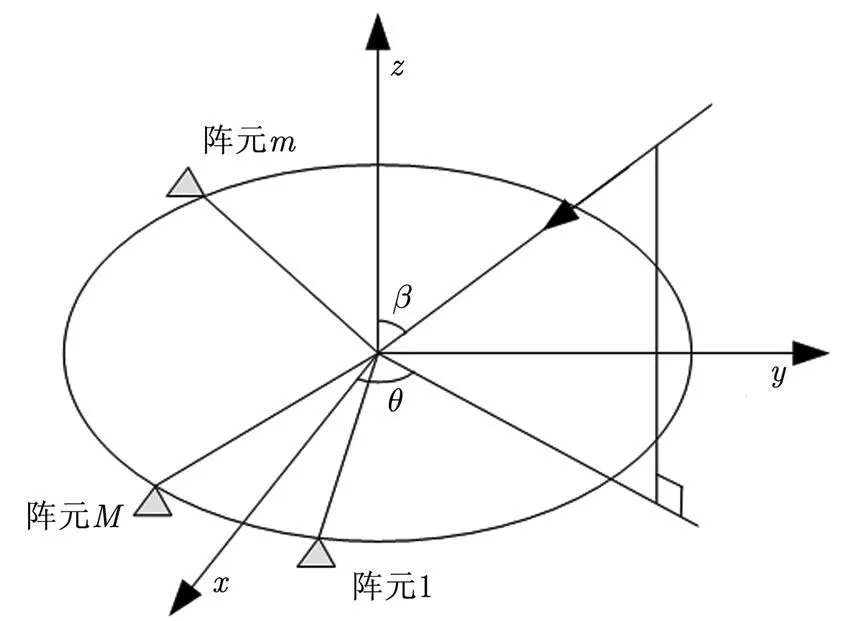
图2 均匀圆阵列结构图

性质2均匀圆阵导向矢量具有对称性，记

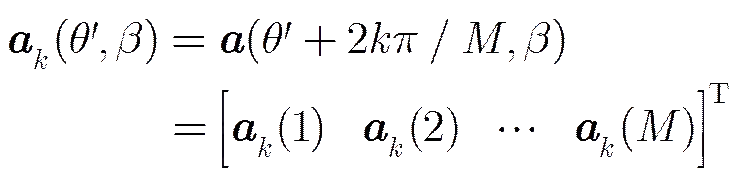
（12）

证明

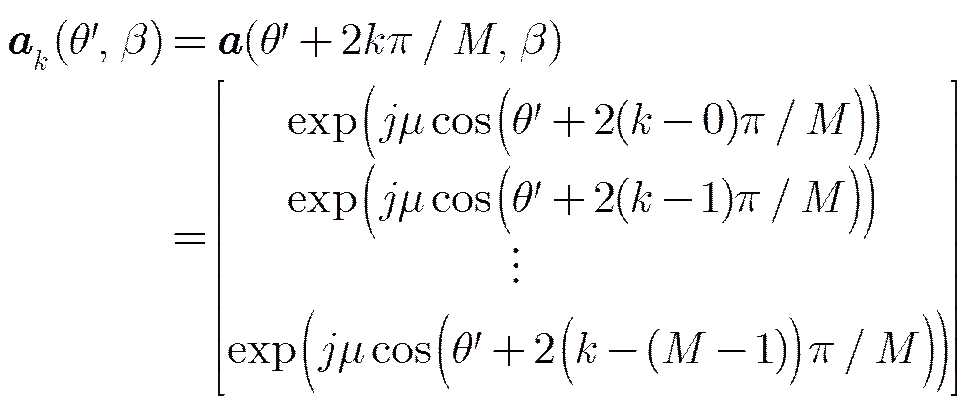
(14)

比较式(13)、式(14)，可得式(12)的结论。

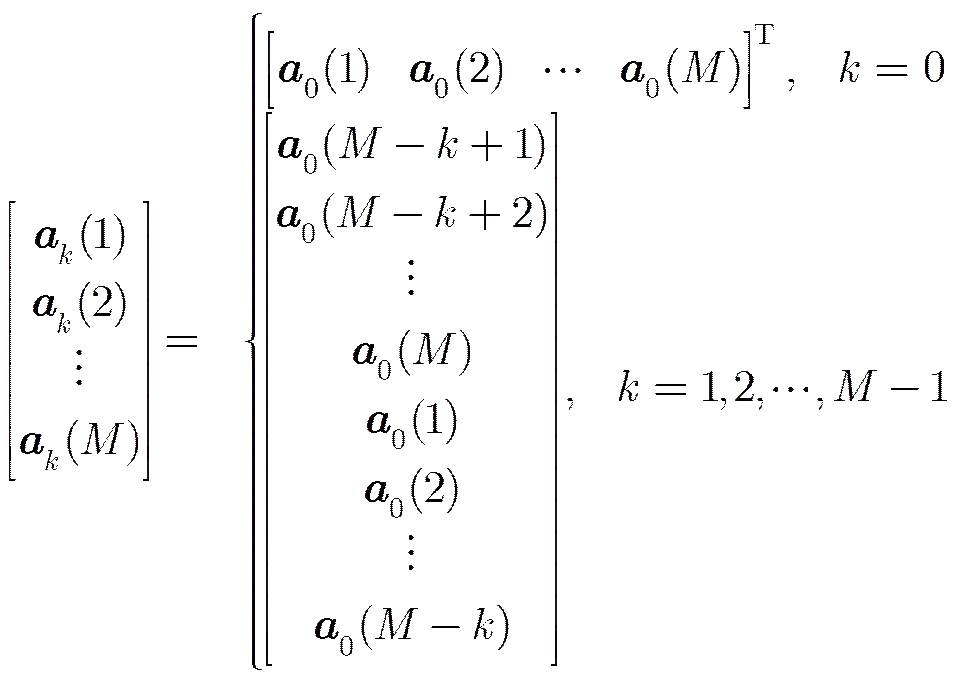
证明

证毕

本质上，性质1-性质3都是由特殊的阵列结构决定的。

3 MUSIC算法的改进

MUSIC算法谱函数复杂，计算量大，而且包含一些冗余运算。MUSIC算法谱函数定义为

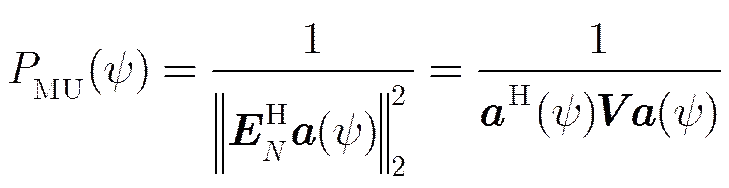
(18)

分别令：

(20)

(21)

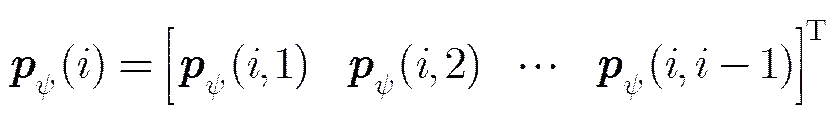
(23)

(24)

再令：

(26)

(28)

(29)

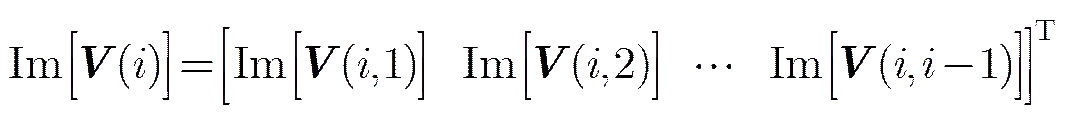
(31)

3.1 均匀线阵MUSIC算法改进

同理可得

（35）

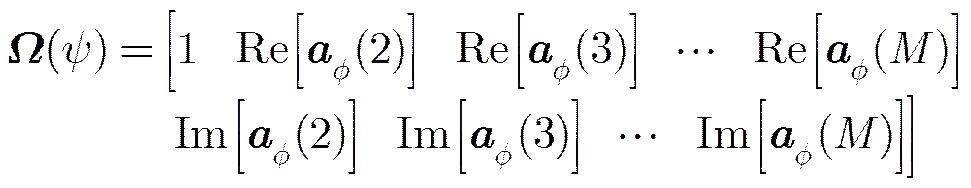
(37)

其中

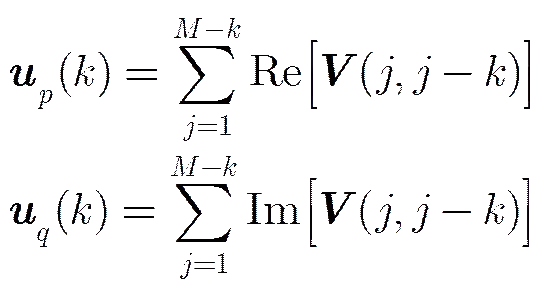
则

(38)

式(38)与式(31)计算结果完全一致，但较式(31)的计算量更少。以元线阵为例，按式(31)需要/2次乘法，而按式(38)仅需次乘法运算。

3.2 均匀圆阵MUSIC算法改进

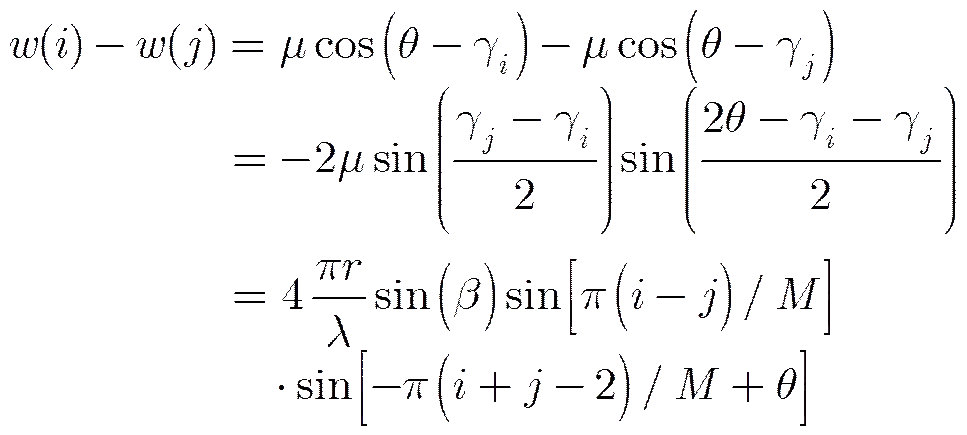
令

(40)

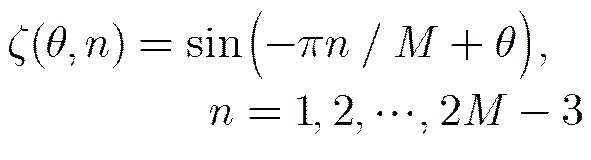
可得

(42)

同理

表1 改进前后乘法运算次数

标准MUSIC算法改进后(圆阵)改进后(线阵)

4 改进的查表法

MUSIC算法表示的是连续谱，但工程中只在有限的离散方向点上计算其离散谱，称之为离散MUSIC(Discrete MUSIC，简称DMUSIC)算法，DMUSIC算法与离散傅里叶变换(Discrete Fourier Transform，简称DFT)的物理意义是相通的。MUSIC算法的三角函数求值运算量巨大，DMUSIC算法也是如此，为降低DMUSIC算法的计算量，可以采用查表的方法代替三角函数求值运算。查表法就是在DFMUSIC算法的抽样方向上对或进行制表，运行时再对其进行查表，从而完全避免了三角函数求值运算。

查表法需要的存储量比较大，对于2维阵列，其存储量的需求一般都达到数百兆至数吉比特。要扩大查表法的应用范围，必须降低其存储量需求。前面，我们给出了典型阵列导向矢量的一些性质，利用这些性质可以对查表法进行改进，减少其对存储量的要求。

4.1 均匀线阵情形

对于均匀线阵，由性质1可得

（45）

因此

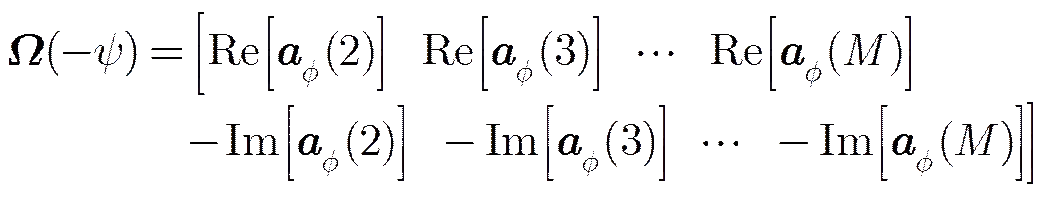
4.2 均匀圆阵情形

对于均匀圆阵，记

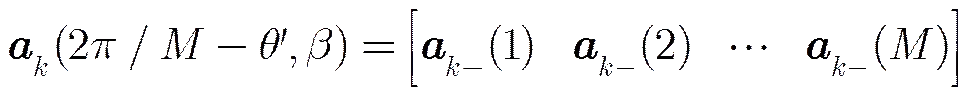
由性质2可得

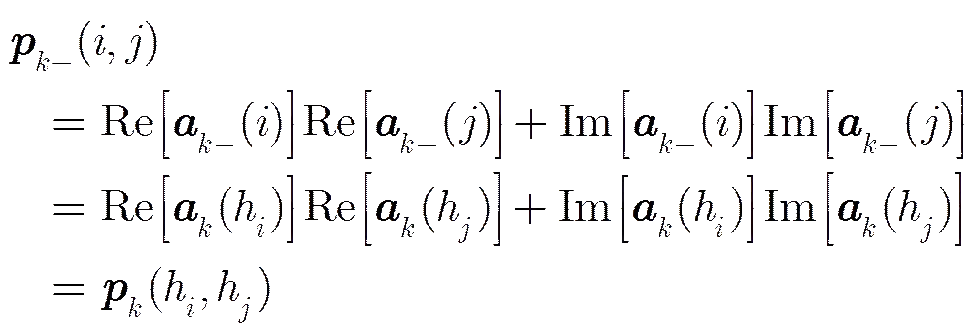
(49)

以五元阵列为例，按0.3°步进作谱估计，4 byte的数据精度(float型数据)，均匀线阵和均匀圆阵的存储空间需求见表2。总体来说，均匀线阵需要的存储空间非常小，以KB为数量级，而均匀圆阵需要的存储空间比均匀线阵大很多，以MB为数量级。

表2 均匀线阵和均匀圆阵的存储空间需求

均匀线阵查表法(byte)均匀圆阵查表法(byte)

5 仿真分析

仿真1 八元均匀线阵，相邻阵元间隔为0.15 m，空间有两个不相关的信号源入射，入射信号波长为0.3 m，入射角度分别为-45°和30°，信噪比为0 dB，接收机采样快拍数为200，仿真软件为MATLAB 7.0。做300次蒙特卡洛试验，统计300次试验耗时总时间，见表3；标准MUSIC算法查表法谱估计结果完全一致，图3是它们某次谱估计的结果。

表3 谱估计耗时比较(300次总计)

步进标准MUSIC算法(s)本文改进的查表法(s) 0.01°95.158 1.561 0.05°19.105 0.321 0.1° 9.610 0.156 0.3° 3.173 0.052

纵向比较，理论上，0.01°步进耗时是0.05°步进耗时的5倍、是1°步进耗时的10倍、是0.3°步进耗时的30倍，实际耗时倍数与理论耗时倍数基本一致。横向比较，标准MUSIC算法谱估计耗时超过查表法的60倍，查表法的优势非常明显。可以看出，精确谱估计需要的代价很大，实时性较差；标准MUSIC算法很难满足工程需要，但是本文的查表法大幅提高了MUSIC算法的实时性。

仿真2五元均匀圆阵，半径为0.15 m，空间有两个不相关信号源，波长为0.3 m，来波方向分别为(60°, 30°)和(240°, 30°)，信噪比为0 dB，方位角步进和俯仰角步进相同，接收机采样快拍数为200。为比较标准MUSIC算法、改进的查表法和文献[12]提出的两种查表法：直接查表法、间接查表法，利用Visual C++6.0进行100次实验，统计谱估计平均耗时，结果见表4；将谱估计结果保存到文件中，利用MATLAB软件观看谱估计结果，4种谱估计算法结果完全一致，图4是谱估计结果。

表4 谱估计耗时比较(100次平均)

步进标准MUSIC算法(s)本文改进的查表法(s)文献[12]直接查表法(s)文献[12]间接查表法(s) 0.1°63.6211.1361.1346.236 0.3°7.0820.1240.1250.694 0.5°2.6340.0470.0480.252 1.0°0.6460.0120.0130.060

纵向比较，可以获得和仿真1相同的结论。横向比较，改进的查表法和直接查表法谱估计耗时相近；标准MUSIC算法谱估计耗时是改进查表法和直接查表法的50–60倍，是间接查表法的10倍以上。标准MUSIC算法耗时最为严重，间接查表法次之，直接查表法和改进的查表法耗时最少。通过谱估计图可以看出改进的查表法谱估计准确性较好。

仿真3五元均匀圆阵，半径为0.15 m，假设入射信号波长为0.3 m，方位角步进和俯仰角步进相同，采用Visual C++6.0软件编程。用自编的函数Nnew对库函数new进行封装，用以统计查表法制表所占用的内存，数据类型为float型，统计结果见表5。

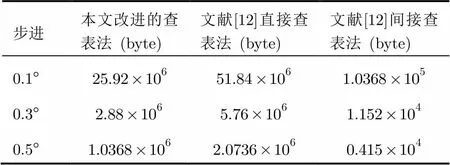
表5 制表占用内存大小比较

从统计结果可以看出，直接查表法占用内存是改进查表法的两倍，而间接查表法仅需很小的内存。随着谱估计精度的提高，查表法占用的空间急剧增加。精确谱估计的代价不仅表现在时间上，也表现在所占用的内存空间上。

6 总结

以往的快速高分辨空间谱估计算法没有从根本上解决计算量问题，查表法提供了一种可行的途径。通过分析均匀线阵和均匀圆阵两种典型阵列的阵列结构，发现均匀线阵导向矢量具有共轭对称性，均匀圆阵导向矢量具有周期循环性和对称性；在降低MUSIC算法的乘法运算次数的基础上，对查表法进行改进。改进的查表法利用导向矢量的性质降低了查表法对存储量的需求，同时保持了较快的运算速率。

本文以MUSIC算法为例，提出降低计算量的一种思路，该思路可以推广到其它空间谱估计算法中。要进一步提高空间谱估计算法的实时处理能力还可以从多方面改进，如根据不同方向的分辨率调整搜索步进、利用先验知识缩小搜索范围等。

[1] 张小飞, 汪飞, 徐大专. 阵列信号处理的理论和应用[M]. 北京: 国防工业出版社, 2010, 第4.3节.

Zhang Xiao-fei, Wang Fei, and Xu Da-zhuan. Array Signal Processing Theory and Application[M]. Beijing: National Defense Industry Press, 2010, Section 4.3.

[2] 郭跃. 超分辨波达方向估计技术的研究[D]. [博士论文], 华中科技大学, 2007: 4-5.

Guo Yue. Research on direction of arrival estimation with super resolution[D]. [Ph.D. dissertation], Huazhong University of Science and Technology, 2007: 4-5.

[3] Zhuang Jie, Li Wei, and Manikas A. An IDFT-based root-MUSIC for arbitrary arrays[C]. 2010 IEEE International Conference on Acoustics, Speech and Signal Processing, Dallas, Texas, USA, May 22-27, 2010: 2613-2617.

[4] Tripathy Praveen, Srivastava S C, and Singh S N. A modified TLS-ESPRIT-Based method for low-frequency mode identification in power pystems utilizing synchrophasor measurements[J]., 2011, 26(2): 719-727.

[5] 庄学彬, 陆明泉, 冯振明. 一种数值稳健且低复杂度的信号子空间估计新方法[J]. 电子与信息学报, 2011, 33(1): 90-94.

Zhuang Xue-bin, Lu Ming-quan, and Feng Zhen-ming. A numerically robust and low-complexity method of signal subspace estimation[J].&, 2011, 33(1): 90-94.

[6] Azarbar A and Dadashzadeh G. A new DOA estimation based on direct data domain algorithm[C]. 2011 IEEE GCC Conference and Exhibition, Dubai, United Arab Emirates, Feb. 19-22, 2011: 205-208.

[7] Paine A S. Fast MUSIC for large 2-D element digitised phased array radar[C]. 2003 IEEE Rader Conference, Adelaide, Australia, May 5-8, 2003: 200-205.

[8] Liu Lu-tao, Si Xi-cai, and Wang Li-guo. Fast subspace DOA algorithm based on time-frequency distributions without eigen decomposition[C]. 3rd International Conference on Measuring Technology and Mechatronics Automation, Shanghai, China, Jan. 6-7, 2011, 2: 170-173.

[9] 邓键敏, 吴瑛. 基于MH抽样逐次搜索的快速MUSIC 算法[J]. 计算机工程与设计, 2010, 31(20): 4508-4511.

Deng Jian-min and Wu Ying. Fast MUSIC algorithm via metropolis-hastings sampler and sequential searching[J]., 2010, 31(20): 4508-4511.

[10] Minseok Kim, Koichi Ichige, and Hiroyuki Arai. Implementation of FPGA based fast DOA estimator using unitary MUSIC algorithm [C]. 2009 IEEE Rader Conference, California, USA, Apr. 20-22, 2009: 4-8.

[11] 董照飞. 基于DSP的MUSIC 算法的实现[J]. 现代电子技术, 2006, 23(7): 21-23.

Dong Zhao-fei. The realization of MUSIC arithmetic based on DSP[J]., 2006, 23(7): 21-23.

[12] 张兴良, 阮怀林, 王树亮. 圆阵列MUSIC 算法快速测向技术[J]. 数据采集与处理, 2011, 26(3): 374-378.

Zhang Xing-liang, Ruan Huai-lin, and Wang Shu-liang. A fast direction finding technology based on MUSIC algorithm with circular array[J].&, 2011, 26(3): 374-378.

[13] Wang X and Zhang X P. Optimal look-up table-based data hiding[J]., 2011, 5(2): 171-179.

[14] Zhang Q T. Probability of resolution of the MUSIC algorithm [J]., 1995, 43(4): 978-987.

Study on Fast MUSIC Algorithm with Typical Array

Zhang Xing-liang Wang Ke-ren Fan Fu-hua

(Department of Information Engineering, Electronic Engineering Institute, Hefei 230037, China)

Because MUSIC (MUltiple SIgnal Classification) algorithm needs a large number of multiplications and trigonometric function evaluations, it is weak in the real time processing. This paper is aim at resolving above problem. Firstly, by analyzing the structural features of the uniform circular array and the uniform linear array, some properties of steering vector are extracted. Then, the properties of Hermite matrix are employed to decompose the complex multiplication, and then two real vectors are constructed to reduce the number of multiplications. Finally, with the properties of steering vector, a new algorithm based on look-up-table is proposed. The new algorithm neither has any trigonometric function evaluation, nor requires much memory space. The result of simulation experiments shows that the new algorithm raises the rate of MUSIC algorithm more than 50 times, while ensures the same estimated results. Therefore, the new algorithm has a wide application prospect.

Typical array; Steering vector; Look-up-table method; Fast MUSIC (MUltiple SIgnal Classification) algorithm

TN911.7

A

2095-283X(2012)02-0149-08

10.3724/SP.J.1300.2012.20026

2012-04-23收到，2012-06-13改回；2012-06-20网络优先出版

国家自然科学基金 (61171170) 资助课题

张兴良 305755450@qq.com

张兴良(1985-)，男，安徽合肥人，博士生，研究方向为雷达信号处理、智能天线。

E-mail: tianyawubian@sina.com

王可人(1957-)，男，江苏镇江人，教授，博士生导师，总参某站主任，研究方向为通信信号处理、雷达信号处理。

E-mail: wangkeren0512@126.com

樊甫华(1975-)，男，安徽芜湖人，讲师，研究方向为雷达信号处理。

E-mail: davidfaneei@163.com