基于DSP的直线感应电动机矢量控制

卞林玉，陈志辉

(南京航空航天大学，江苏南京210016)

0引 言

直线电动机将电能直接转换成直线运动机械能，在很大程度上简化了系统结构，且控制简单、维护方便，因而在国民经济各个部门都获得了应用，已经成为国际学术界研究的重要课题［1-2］。原理上，直线感应电动机与传统旋转感应电机都是通过三相交流电产生的磁场与导体作用产生驱动力，因而，用于旋转感应电机的控制方法也同样适用于直线感应电动机。但由于直线感应电动机结构的特殊性及种类繁多，难以总结出统一且简单的数学模型，对其进行准确控制比较复杂［3］，因此，推导出较为准确的数学模型十分关键。本文以双边长初级短次级直线感应电动机为研究对象，根据实际结构分析推导出数学模型，同时考虑到因铁心开断而引起的端部效应，对旋转感应电机矢量控制策略进行修正，并进行了建模仿真和系统实验，取得了较为满意的效果。

1直线感应电动机的数学模型及其控制策略

本文所研究的电机为长初级短次级直线感应电动机，如图1所示。初级绕组分为两个部分:覆盖着次级的部分称为有效部分，电机能量的转换主要是通过这部分实现的;其余部分称为无效部分，它们对电机能量的转换无任何作用。样机的初级绕组采用串联形式，绕组中流过的电流大小一样，但有效部分的气隙磁密要比无效部分的气隙磁密小得多［4］。同时，直线电动机铁心的开断和绕组的不连续使得各相绕组所处磁场有差异，存在着端部效应:当次级相对初级做直线运动时，次级将感应出与励磁电流方向相反的涡流。这将使直线电机的损耗增加，功率因数降低，推力减小，特别在高速低转差率运行的直线电机中更为明显［5-6］。

图1 短次级直线感应电动机示意图

根据上述分析，可以得出直线感应电动机的等效电路，如图2所示。其中a为次级长度和初级长度的比值，修正电感=aLm［1-f(Q)］来补偿因涡流引起的励磁电流的减小，引入等效电阻aRrf(Q)来等效端部效应引起的功耗［7-8］。

图2 直线感应电动机的等效电路

在按次级磁场定向的同步旋转坐标系中，规定d轴沿着次级总磁链矢量λr的方向。对于鼠笼型转子电机，转子短路，有Udr=Uqr=0。则同步旋转坐标系下直线感应电动机数学模型如下:

电压方程:

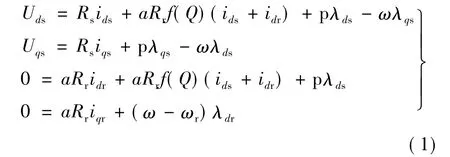
磁链方程:

有效部分初级磁链:

运动方程:

矢量控制的基本思想是:将三相电流ia、ib、ic进行坐标变换，分解为励磁电流分量ids和电枢电流分量iqs，通过控制互不耦合的ids和iqs来控制电机次级磁通 λdr和电磁推力 Fe［9-10］。

由上述数学模型可以推导得出:

很明显，控制励磁电流分量ids即可实现对次级磁通λdr的控制。而由于端部效应的存在，推力Fe与电枢电流分量iqs之间并不是简单的比例关系。这里，为了实现对Fe的控制，本文在矢量控制系统模型中对 iqs进行了补偿［11-13］，即:

2直线感应电动机的Simulink仿真

直线感应电动机矢量控制系统模型包括电机本体模型、磁链观测器模型和控制器模型三个部分，其整体仿真结构图如图3所示。

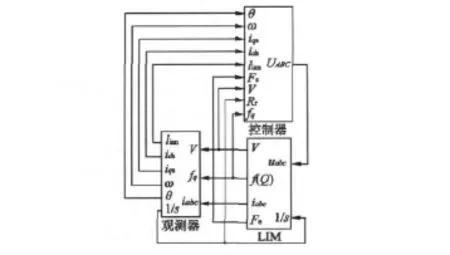
图3 直线感应电动机矢量控制系统整体模型

位置给定初始值为0．42 m，0．15 s时跃变为0 m，实现一次往复运动，仿真波形如图4所示。图4(a)为次级位置输出，其中虚线为位置给定。从图中可以看出，空载时位置给定的改变很快引起了系统输出位置的响应，平均响应时间为0．06 s，并且稳态误差小于0．012%。q轴电流变化趋势与图4(b)中推力变化趋势相一致，符合控制iqs控制电磁推力Fe的规律。

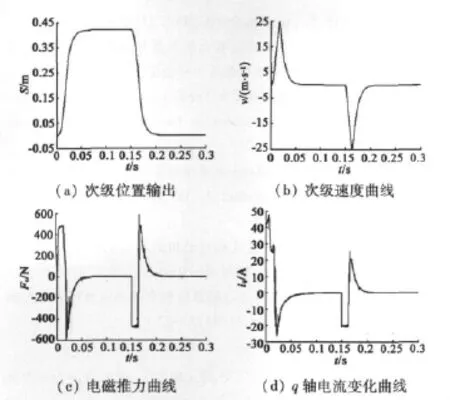
图4 空载时位置闭环控制仿真曲线

3直线感应电动机全数字矢量控制系统

基于DSP的直线感应电动机矢量控制系统主要由功率电路、控制系统及辅助电路组成。功率部分由整流电路、滤波电路、逆变电路、能耗制动电路以及保护电路组成。控制系统由TMS320F2812芯片及其外围电路组成，用来完成矢量控制核心算法、SVPWM产生、相关电压电流的检测处理等功能。辅助电路由辅助开关电源、电流传感器、位置传感器组成，以实现给系统提供多路直流电源、电机速度检测、电流检测等。直线感应电动机矢量控制系统框图如图5所示。

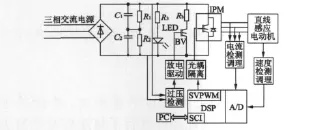
图5 直线感应电动机矢量控制系统框图

矢量控制系统软件采用中断服务程序处理结构，由主程序和中断服务子程序构成。中断服务子程序包括主中断程序、SCI通信中断程序和故障中断程序。程序流程如图6所示。

中断程序利用定时器1的下溢中断，每100 μs进入一次中断。在中断程序中，完成电流采样、坐标转换、PID调节、速度计算、磁链角计算和 SVPWM产生等。其中，用于坐标转换的磁链角为前一周期计算值。

4实验结果与分析

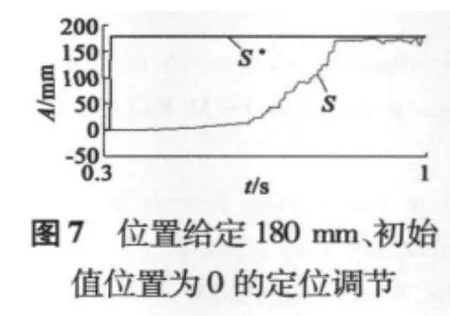
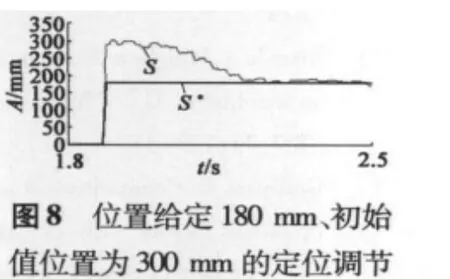
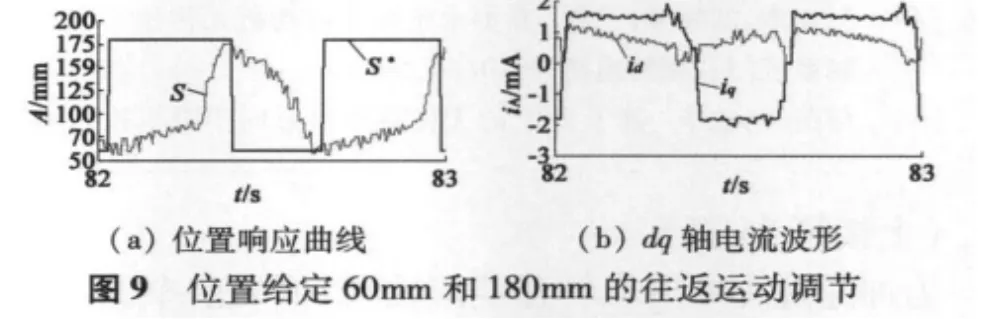
位置PID调节波形如图7、图8、图9所示。其中图7是位置给定180 mm、初始位置为0的定位调节，其位置响应时间小于1 s，定位误差为5 mm;图8是位置给定180 mm、初始位置为300 mm的定位调节，其位置响应时间为0．5 s，定位误差为3 mm;图9是位置给定60 mm和180 mm的往返运动调节，0．7 s实现往返运动一次，定位误差为2 mm;正向移动时q轴电流为正，反向移动时q轴电流为负，符合通过控制q轴电流来控制电磁推力的矢量控制规律。从实验结果可以看出，电机定位误差小于5 mm，考虑到传感器误差及AD采样误差的存在，可认为本控制系统定位可靠。往返运动误差也小于5 mm，能可靠实现往返循环运动控制。

图6 程序流程图

5结 语

本文对双边长初级短次级直线感应电动机进行了结构分析，将电机初级分为有效部分和无效部分，推导出该电机的数学模型及等效电路，并考虑其端部效应，设计出直线感应电动机矢量控制系统。仿真结果验证了系统的可行性，并以此为基础搭建了实验平台，实验结果表明，该控制系统能实现电机可靠定位与往返运动功能，电机定位误差小于5 mm，考虑到传感器误差及AD采样误差的存在，可认为本控制系统定位可靠，也为进一步深入研究打下了基础。

［1］ 王伟进．直线电机的发展与应用概述［J］．微电机，2004，37(1):45-47．

［2］ 叶云岳．直线电机原理与应用［M］．北京:机械工业出版社，2000．

［3］ 刘少克，张文雅．直线感应电动机控制方法概述［J］．微特电机，2006(8):35-41．

［4］ 龙遐令．直线感应电动机的理论和电磁设计方法［M］．北京:科学出版社，2006．

［5］ Sung Jeong-hyoun，Nam Kwanghee．A new approach to vector control for a linear induction motor considering end effects［C］．Thirty-Fourth IAS Annual Meeting on Industry Applications，1999，4:2284-2289．

［6］ Kim D K，Kwon Byung-II．A novel equivalent circuit model of linear induction motor based on finite element analysis and its coupling with external circuits［J］．IEEE Trans．on Mag，2006，42(10):3407-3409．

［7］ 徐伟，孙广生．单边直线感应电机纵向边缘效应的研究［J］．中国工程科学，2007，9(3):21-27．

［8］ 任晋旗，李耀华，王珂．动态边端效应补偿的直线感应电机磁场定向控制［J］．电工技术学报，2007，22(12):61-65．

［9］ 贾宏新，林瑞光．直线感应电动机矢量控制系统的仿真研究［C］//2002年全国直线电机学术年会论文．2002:114-118．

［10］ da Silva E F，dos Santos E B．Vector control for linear induction motor［J］．IEEE Transactions on Energy Conversion，2008，23(3):789-795．

［11］ Kang G，Nam K．Field-oriented control scheme for linear induction motor with the end effect［J］．IEE Proc．Electric Power Appl．，2005，152(6):1565-1572．

［12］ 王飞飞，黄斌，胡波．直线感应电机磁场定向控制系统仿真［J］．大功率变流技术，2008(6):30-37．

［13］ 姚保庆，范瑜，吕刚．考虑边端效应的直线感应电机矢量控制研究［J］．微电机，2006，39(9):29-32．