全数字化步进电动机细分驱动器设计

谢国钢，王念兴，李小海，姜淑忠

(1．上海交通大学，上海200240;2．大庆油田装备制造集团研究院，黑龙江大庆163312)

0引 言

步进电动机是一种通过电脉冲信号控制相绕组电流实现角度控制的机电执行元件，与其他类型电机相比，具有易于开环精确控制、无积累误差等优点，在众多领域中获得了广泛的应用。细分驱动技术是一种有效改善步进电动机低频特性和提高步进精度的驱动技术，且可以减小或消除振荡、噪声和转矩波动。

传统的步进电动机系统主要包括单片机、D/A模块、斩波比较电路、驱动及功放电路、步进电动机等几部分［1］，具有以下缺点:

(1)器件多，故障率较高、成本高;

(2)开关频率不确定，容易导致功率器件过热;

(3)不能实现驱动器件对上位机命令的加减速控制，增加上位机的软件工作量;

(4)细分数小，不能很好地抑制振动、失步现象;

(5)不能实现闭环控制，无法满足更高精度要求。

目前市场上已有很多高性能、功能强大的微处理器，能承担步进电动机系统的大部分信息处理，可将系统简化为微处理器、驱动及功放电路、步进电动机等三个主要部分，实现全数字化处理，很大程度上克服了上述传统系统的五个缺点，使步进电动机系统的性能大幅度提高。本文设计了基于48脚ARM芯片STM32F103的全数字化步进电动机细分驱动器。

1系统总体设计

1．1 系统硬件

图1为本文设计的系统硬件框图，主要包括STM32F103芯片、IR驱动芯片及H桥、步进电动机，以及功能选择拨位开关、电流采样电路、供电电路、编码器和控制输入电路。为了提高系统的可扩展性和人机交互能力，还配置了CAN、RS485通讯接口和E2PROM。

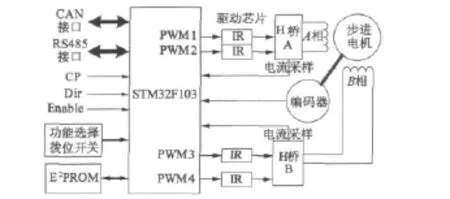
图1 系统硬件框图

STM32F103芯片是该系统的核心，主要功能为根据给定输入信号运算出细分驱动控制数据，输出至后续环节，另外还实现系统的电流闭环、位置闭环、保护、通讯等功能。驱动芯片和 H桥接受STM32F103芯片的控制信号，对电机进行细分驱动。步进电动机为二相混合式，转子齿数或极对数p=50。功能选择拨位开关决定细分数、电流大小、单双脉冲模式，给定输入端口CP、Dir、Enable分别是脉冲、方向、使能信号的输入口。传统步进电动机细分驱动的电流闭环控制通过硬件模拟电路实现，且都为位置开环控制。本文设计的全数字化驱动控制通过电流采样、STM32F103芯片处理实现电流闭环，并充分利用STM32F103芯片资源，增加编码器实现位置闭环控制，以优化系统的性能，减少失步、过冲现象，有效抑制振荡、噪声和转矩波动。

1．2 系统软件

STM32F103芯片是系统的核心，承担了步进电动机控制的大部分信息处理。图2为本文设计的由STM32F103实现的系统控制架构。

单脉冲工作模式时，CP、Dir分别为上位机输入到本驱动系统的脉冲和方向信号，CP经加减速控制环节得到CP*，然后经角度计算可以得到每步需要转至的角度θ(绝对位置)，结合编码器反馈的电机实际位置θ*，经PI调节后输入至电流矢量控制环节。I为电流选择模块设定的电流值，结合两相电流采样值的合成值I*，经PI调节输出给电流矢量控制环节。电流矢量控制环节为软件程序的关键，主要根据θ和I经PI后的结果进行计算处理，输出两相电流值Ia、Ib。PWM模块则根据两相电流值及对应关系经验，输出4路PWM。

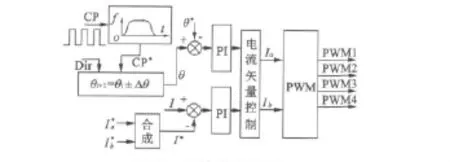
图2 系统控制架构

一般步进电动机驱动器产品不包含加减速控制功能，因此要求上位机负责加减速控制，增加了控制系统的编程难度和软件负担。本文设计由驱动器自身实现加减速控制，控制系统只需发简单的步进脉冲，甚至只需通过通讯方式将运动控制的几个关键数据发给驱动器CPU，即能实现对步进电动机的完整控制，大幅度减少了控制系统的工作量，使控制极为方便。

2电流矢量控制和细分驱动的实现

本文设计系统采用二相永磁式步进电动机，A相绕组电流和B相绕组电流正好相差90°电角度，如图3所示，因此不需要坐标变换处理，A相绕组轴线即为α轴，B相绕组理论轴线即为β轴。

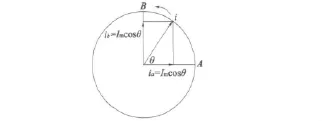
图3 二相步进电动机电流合成矢量

以A相电流为参考，电流合成矢量用复数形式可表示:

这是一个以Im为幅值、θ为辐角的矢量，当θ角变化时，该矢量随之旋转。而电流合成矢量与电机内部合成磁场近似线性相关，因此，只要控制Im恒定、θ角均匀变化，即可实现恒力矩、等步距角的电流矢量驱动控制。

对于两相步进电动机，当采用两相四拍工作方式时，只有 A+B+、A-B+、A-B-、A+B-四步，p=50时，整步步距角:

以1．8°机械角度为步距角运行时，步进电动机振荡、噪声和转矩波动现象较严重，因此需要采用细分驱动技术。其基本思想是控制每相绕组电流的波形，使其阶梯上升或下降，定子磁场的旋转过程中也就有了多个稳定的中间状态，对应于电动机转子旋转的步数增多、步距角减小［2］。

对于两相永磁式步进电动机，设细分数为n，极对数为p，则细分步距角:

本文采用电流矢量恒幅均匀旋转法，即控制每相电流按正弦规律阶梯变化，使得电流合成矢量在空间做恒幅、等距旋转运动［3］。图 4 为细分数n=4时的两相电流正弦式阶梯波形，而p=50，此时:

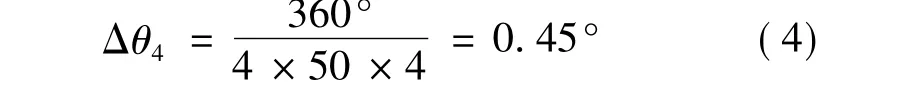
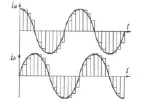
图4 二相步进电动机两相四拍四细分电流波形

增加细分数可减小细分步距角，但细分数也不可能无限增加，要考虑到微处理器的处理能力、步进电动机参数和负载转矩。本文设计的系统最高细分数可达256，即最小细分步距角:

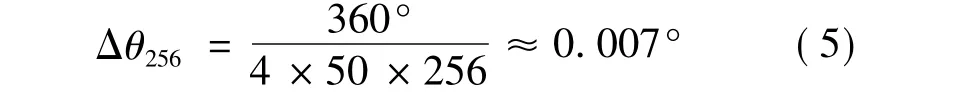
为了简化程序、减少计算量，一般细分控制系统采取预制多个细分数的电流值设定表，在系统运行时查表处理［4］。但是受存储空间的限制，不可能存储太多的细分数电流值设定表，而且要实现不同细分数控制间的无缝切换存在很大困难，无法满足调速性能要求较高的系统。

本系统通过实时计算步进电动机下一步所需电流值，并且储存一个周期计算结果至E2PROM，那么后续周期系统就可以做查表处理了，直至细分数的改变，进入新细分数下的计算、储存、查表。这样，细分数可以任意改变，存储空间占用很少，不同细分驱动之间的切换速度快，增加的计算量也是芯片力所能及的，整个细分驱动性能就大大提高了。

本文控制两相电流的方式是STM32F103芯片实时调整输出到驱动电路的PWM波占空比，即先根据给定信息与闭环反馈信息等计算或查表得到两相电流值Ia、Ib，然后输出对应占空比的PWM波，使两相电流按图4的正弦规律变化。图5为电流矢量控制程序流程图，中断入口为步进动作或细分数改变。计算结果主要包括需给定的两相电流值、电流值对应的PWM波占空比。这种将计算、存储、查表结合为一体的方法，使细分数可以任意取(在微处理器能力范围内)，从而使电流曲线更加平滑，电机性能大大提高。

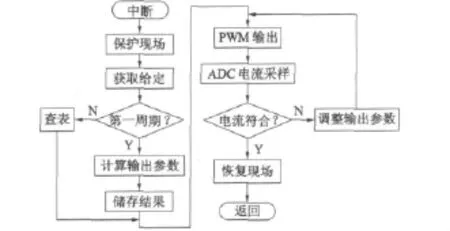
图5 电流矢量控制程序流程图

为保证电流矢量控制的精度，系统采用电流闭环控制。传统的电流闭环电路是主要通过硬件斩波电路实现的，本文将电流闭环也数字化，在各相H桥接地端串接一个0．1 Ω的采样电阻，如图6所示，采样信号经过滤波、放大后输入到STM32103芯片的ADC口，通过STM32F103芯片来实现电流闭环控制，并设计电流PI调节环节，使电流控制更精确。

图6 A相H桥和电流采样电路

3加减速控制和位置闭环

步进电动机驱动执行机构从A点移动到B点的过程中，要经历加速、恒速、减速过程。没有加减速过程容易出现失步和过冲现象，而不合理的加减速控制同样会影响步进电动机的工作效率［5］。

加减速控制曲线主要有直线型、S型、指数型。直线型因受极限频率限制，斜率不能很大，故加速时间较长;S型加减速性能较好，编程较直线型复杂;指数型编程很复杂，占用机时长［6］。综合考虑，本文设计的系统采用S型加减速，如图7所示。

以图7曲线为加减速控制策略，根据运动信息，可以分析出加速、恒速、减速的步数及具体的加减速控制处理方法［7］，加减速控制子程序流程图如图8所示。

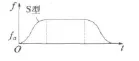
图7 S型加减速曲线

图8 加减速子程序流程图

一般步进电动机控制系统充分利用其开环精度较高而没有配置位置传感器。但是随着科技的发展，很多设备、仪器的精度要求越来越高，除了改进开环控制，位置闭环也早已投入实际应用，而且将是趋势所在。本文采用编码器作为位置传感器，反馈信号直接输入到STM32F163芯片作位置闭环控制处理，实现了电流、位置双闭环控制。

4实验结果

图9 实验波形图

实验中，为体现加减速控制性能，正转半圈(66 ms)、停 10 ms、反转半圈(66 ms)、停 10 ms，周期循环动作。图9为实验中 Dir、Pulse、Ia的波形，下图为上图的一小段时间的放大效果。由图9可直观地看到步进电动机的加减速控制过程，加速、减速过程时间分别为20 ms，旋转半圈耗时 64 ms，共 25个电流周期。恒速旋转时，一个电流周期(4 整步)为1．72 ms，则转速:

实验时在转轴上做定位标记，每转一段时间让电机停止，观察电机位置以判断电机是否出现失步现象。经多次实验，本细分驱动系统能控制步进电动机平稳加速起动、高速运行、减速停止，且保证电机不失步。

5结 语

本文设计的步进电动机驱动器充分利用STM32F103芯片的资源，通过对电流的矢量控制，实现了恒幅、均步的任意细分驱动，并将加减速控制亦集于驱动系统，使上位机控制不用考虑加减速，控制更加方便、简单。增加了位置闭环控制、通讯接口，使系统能够适用于高要求的场合。整个系统以STM32F103芯片为核心，实现了全数字化处理，简化了电路，使系统性能优化，降低了故障率和成本，具有很大的应用价值。

［1］ 蒋庆斌，张建生．用89C52单片机实现反应式步进电机变细分驱动［J］．现代驱动与控制，2006(3):21-22．

［2］ 史敬灼．步进电动机伺服控制技术［M］．北京:科学出版社，2006:38．

［3］ 黄勇，彭强．高稳定性步进电机细分驱动控制系统的设计与实现［J］．微特电机，2008，36(10):34-36．

［4］ 惠晶，肖荣．一种实用的步进电机细分驱动控制系统［J］．微电机，2009，2(10):87-89．

［5］ 王晓明．电动机的DSP控制-TI公司DSP应用［M］．第2版．北京:北京航空航天大学出版社，2009:312．

［6］ 黄法恒，刘利．基于单片机的步进电机升降速及精度控制研究［J］．微电机，2010，43(3):95-97．

［7］ 张海英，胡金高．步进电机运行曲线的优化算法与仿真［J］．微特电机，2010，38(11):16-19．