不同节流方式的滑动轴承油膜静态性能求解

李大英

(重庆工业职业技术学院 机械工程系，重庆 401120)

流体润滑的滑动轴承分为动压、静压及动静压轴承，由于动静压轴承具有动压和静压轴承的优点，近年来得到了迅速发展和广泛应用。关于滑动轴承的润滑机理和承载能力的分析与计算，国内外很多学者作了大量的工作。其中，主要是对动静压油膜轴承的润滑力学方程——Reynolds方程进行求解。求解Reynolds方程常用的方法有解析法和数值法，其中，关于解析法的研究，由于数学上的困难，只能求解诸如无限宽、无限窄轴承的计算问题。采用数值法求解动静压轴承的承载问题，普遍采用有限差分法[1-2]和有限元法[3-4]，近年来，随着流体力学分析软件CFD的广泛应用，也有一些学者将其用于对滑动轴承油膜性能的求解中[5-8]。

滑动轴承中节流器对其油膜刚性和承载能力起着十分重要的调节作用，在滑动轴承油膜静态性能分析求解中，鲜有文献针对不同节流方式给出具体的数值求解方法[9-12]。文中针对毛细管、小孔、滑阀反馈及薄膜反馈等不同节流方式下的轴承油膜性能，分析了其数值求解方法，给出了相应的求解模型，为指导滑动轴承的设计、计算提供有益的参考。

1 滑动轴承油膜性能的无量纲Reynolds方程

动静压混合油膜滑动轴承(图1)无量纲化Reynolds方程为[13]

图1 动静压油膜轴承示意图

(1)

图1中，q为外载荷F与竖直轴线的夹角，(°)；χ为偏位角，轴颈偏心相对于竖直轴线的夹角，(°)；dφ为油膜上某点的角度增量，(°)。

2 Reynolds方程的数值解法分析

2.1 Reynolds方程的离散和间隙函数

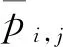
对于动压、静压或动静压油膜轴承，轴承的间隙函数为

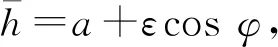
(2)

式中：ε为偏心率，ε=e/h0；e为主轴轴颈与轴承孔的偏心距；a为油腔系数，封油面上a=1，静压腔a为静压腔深度与油膜半径间隙h0之比。

关于Reynolds方程压力场的迭代求解方法可参见文献[13]。

2.2 不同节流方式的连续性方程构建

2.2.1 连续性方程的构造

对于静压轴承或者动静压轴承，由于存在油腔，根据流动连续性原理，可知单位时间内流入油腔的液体体积流量应等于从油腔周边流出的液体体积流量。以图2为例进行分析。

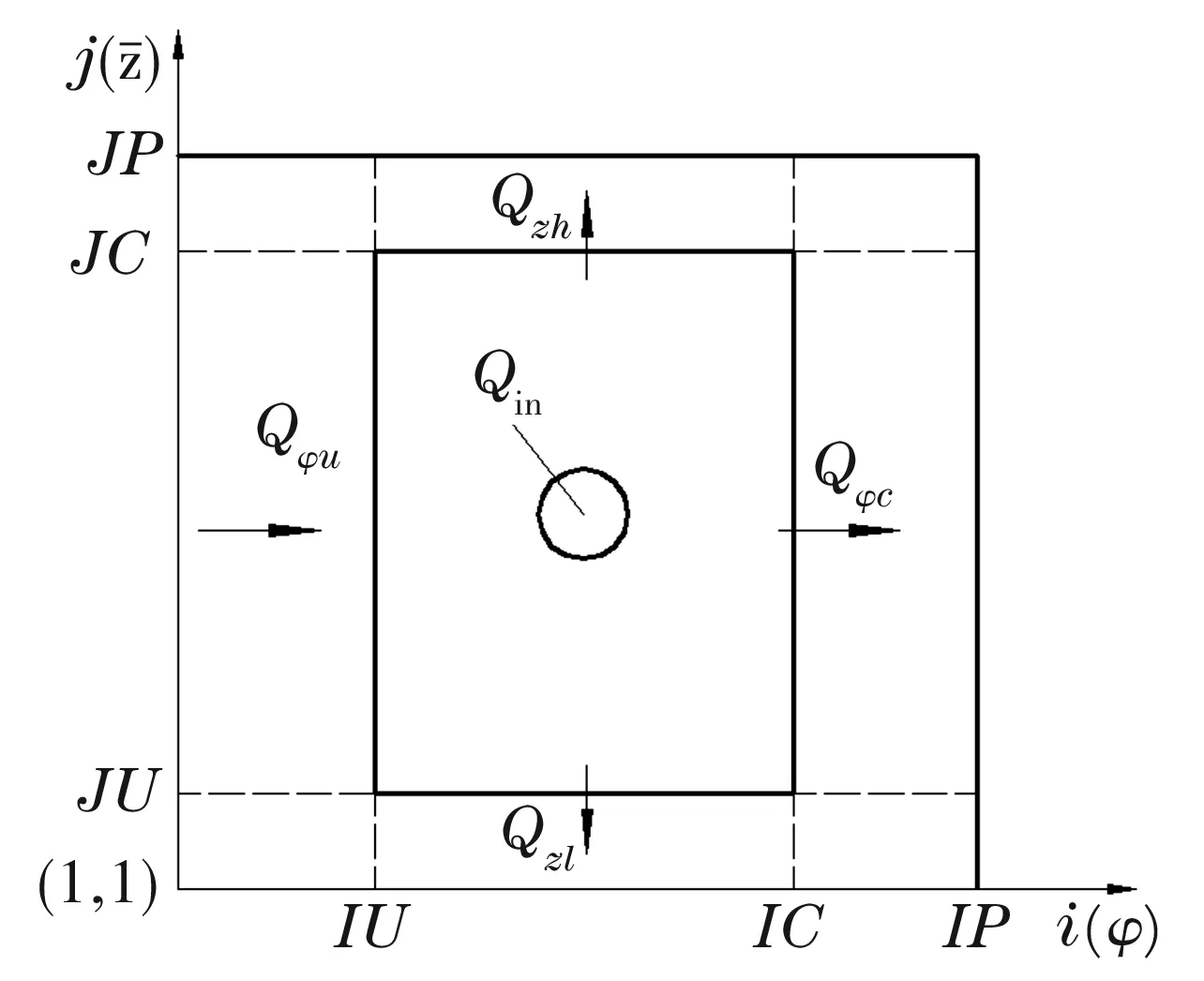
图2 轴承连续性方程分析图

如图2所示，单位时间内无量纲化的流量连续性方程为

(3)

式中：Qin为单位时间内流经节流器的流量，m3/s，采用不同节流装置时流入轴承油腔中的流量是不相同的。表1列举了毛细管、小孔、薄膜及滑阀反馈节流器的流量方程及相关符号。

2.2.2 低松驰迭代及收敛准则

根据 (3) 式及表1可计算出节流后(或油腔)压力边界条件下所得到的轴承油腔压力场，并满足新的节流后的压力，如二者不等，表示设定的压力初值有误，需用低松驰法进行修正，即

表1 不同节流器的图形符号及流经节流器的流量Qin

(4)

收敛准则为

(5)

取δ2=1×10-3，满足 (5) 式时方可结束压力场的迭代过程。

2.3 边界条件的确定

2.4 承载能力计算

对油膜节点压力进行积分，就可得到承载能力，其无量纲表达式为

(6)

承载能力计算时应满足收敛准则

(7)

一般情况下δ1=1×10-3或更小，如果(7)式得不到满足，就表示假设的偏心位置角χ不准确，需修正后重新进行计算，修正式为

(8)

式中：χ(n+1)为新值；χn为原值；ω1为松驰因子。

每修正一次χ值，需重新计算各节点的间隙函数值，求解新的压力场以及载荷大小和方向，直到满足收敛准则为止。最后在已确定的轴心平衡位置上计算轴承的摩擦功耗、流量及油泵功耗等其他性能参数。

2.5 油膜等温计算

设润滑油经过节流器入口的温度为tin，则油膜有效温度tm为

tm=tin+βΔt,

(9)

式中：β为系数，高速状态时β=1，中、低速状态下β=0.8。

开始计算时需假设油膜的有效温度tm0，由此可求得轴承油膜压力分布及摩擦力，再根据热平衡方程求得计算条件下的油膜有效温度tm，如二者不等，则说明假设的tm0有误，需进行修正，修正判据为

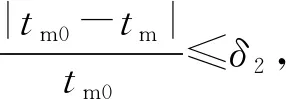
(10)

式中：δ2为计算精度。

3 示例分析

3.1 已知条件

图3所示为两种结构形式的轴承(图3a采用毛细管和小孔节流，图3b采用毛细管、小孔、滑阀反馈和薄膜反馈节流)，采用HU-N46数控机床液压油。已知参数见表2，节流器参数见表3。

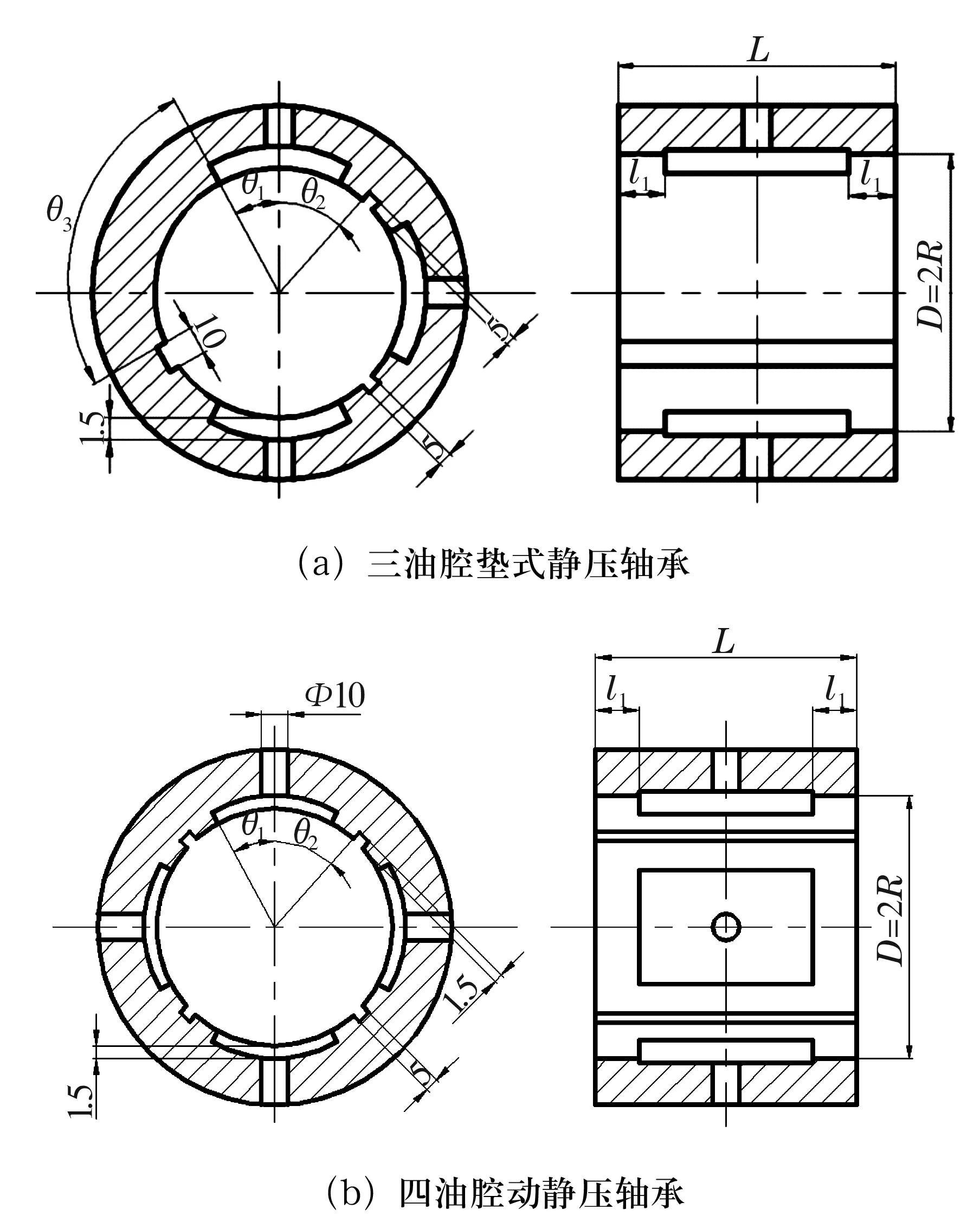
图3 静压、动静压油膜轴承结构图

表2 基本参数表

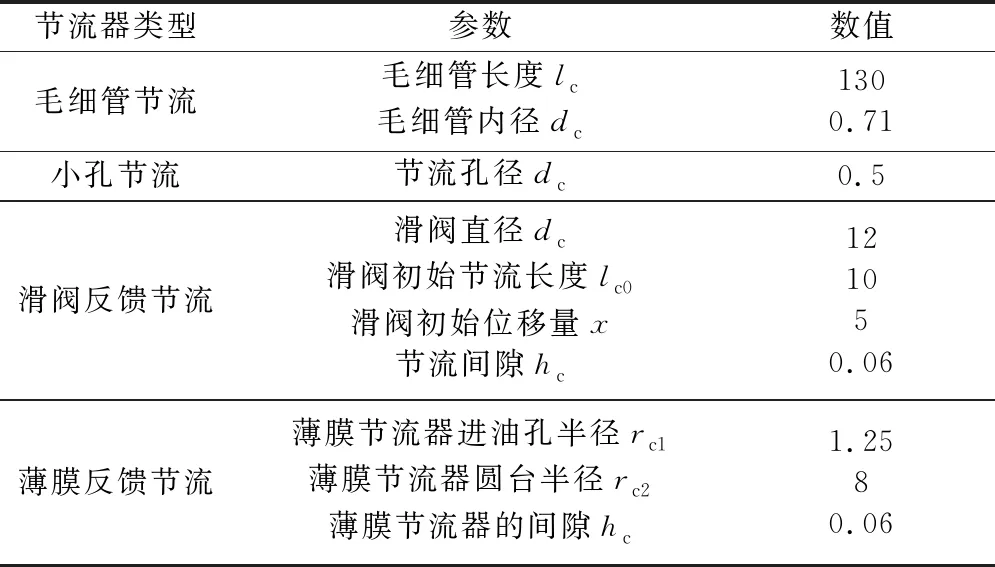
表3 节流器参数 mm

3.2 数值计算结果及分析

将表2、表3中的已知参数代入上述数学模型，求得轴承油膜静态性能的数值解，获得不同节流方式下三油腔动静压油膜轴承的压力分布(图4)及四油腔垫式静压轴承静态性能(表4)。

表4 不同节流方式下四油腔垫式轴承油膜静态性能对比分析

根据图4并进行承载能力计算，当偏心率ε=0.2时，采用毛细管节流的承载能力为8 187 N，而采用小孔节流的承载能力为10 200 N，这说明采用小孔节流的动静压综合承载能力稍高于毛细管节流。而根据图4分析可知，采用毛细管和小孔节流时，动压腔中的动压效果基本相当，动压效应主要取决于速度和油楔形状。节流方式主要调节的是静压效应。

由表4可知，采用薄膜反馈节流、滑阀反馈节流在偏心量ε=0.01时具有较高的承载能力，而采用毛细管和小孔节流在偏心率ε=0.2时才能达到薄膜反馈、滑阀反馈在极小偏心率下的承载能力，这说明滑阀和薄膜反馈节流具有较高的油膜承载能力及油膜刚度，这是因为滑阀与薄膜反馈节流是可变节流，而毛细管与小孔节流属于固定节流，轴承的承载能力和油膜刚度远远低于可变节流的轴承。同时，小孔节流轴承的油膜刚度和承载能力稍高于毛细管节流的轴承。

4 结论

(1)建立了毛细管、小孔、滑阀反馈和薄膜反馈等4种不同节流方式下轴承油膜性能数值计算的数学模型。

(2)不同节流方式主要是调节和改变轴承油腔的静压力，使轴承具有不同的静态刚度，对轴承的动压力影响较小。

(3)在相同工况下，毛细管、小孔节流下的轴承承载能力比滑阀、薄膜反馈节流的承载能力小得多。