基于离散时间无差拍的无轴承异步电动机SVM-DTC系统
2012-07-20刘贤兴陈虎周进伟杨泽斌
刘贤兴,陈虎,周进伟,杨泽斌
(江苏大学 电气信息工程学院,江苏 镇江 212013)
无轴承异步电动机由于弱磁容易、结构简单和可靠性高等特点得到普遍的重视。目前对无轴承异步电动机的控制方法主要有矢量控制[1-3]和直接转矩控制[4]。采用直接转矩方法控制无轴承异步电动机,可以使转矩控制绕组不再受到矢量控制算法的制约,从而克服了矢量控制算法的局限性[4]。而且悬浮控制绕组所需要的转矩绕组气隙磁链可由直接转矩控制算法中已辨识好的定子磁链减去定子漏磁得到,无需再设置磁链观测器或采用探测线圈等方法来获得磁链信息,从而降低了系统的成本。
与普通的异步电动机相比,无轴承异步电动机对转矩的脉动更加敏感,而传统的直接转矩控制算法容易产生抖颤。为了减小转矩脉动,文献[5-6]针对异步电动机提出了SVM-DTC控制策略,但是该策略需求解复杂的正交方程。文献[7]提出一种转矩和磁链跟踪与预测相结合的方法,该方法同时考虑了转矩与磁链的无差拍控制,但存在计算量大等问题。
文中研究了基于离散时间无差拍(DTDB)的无轴承异步电动机SVM-DTC控制算法。
1 无轴承异步电动机的数学模型
无轴承异步电动机的定子中放入了两套不同极对数的绕组,一套为转矩控制绕组(极对数为np1,同步旋转角速度为ω1);另一套为悬浮控制绕组(极对数为np2,同步旋转角速度为ω2)。只有当np1=np2±1,ω1=ω2时,才能产生可控悬浮力。无轴承异步电动机的数学模型主要包括旋转部分和悬浮部分方程。下标1,2分别表示旋转部分和悬浮部分的参数。
1.1 旋转部分
无轴承异步电动机旋转部分在两相同步旋转坐标系中的状态方程为
(1)
(2)
(3)
(4)
(5)
式中:ωr为转子角速度;Te为电动机的转矩;TL为负载转矩;J为转动惯量;ψ1sd,ψ1sq分别为定子d,q轴磁链;R1s,R1r分别为定、转子电阻;i1sd,i1sq分别为定子d,q轴电流;u1sd,u1sq分别为定子d,q轴电压;σ为电动机漏磁系数;T1r为转子电磁时间系数;L1s,L1r分别为定、转子电感。
电动机的转矩方程为
Te=np1(ψ1sdi1sq-ψ1sqi1sd) 。
(6)
1.2 悬浮部分
悬浮力方程为

(7)

偏心磁拉力方程为
(8)

运动方程为
(9)
(10)
式中:Fzx,Fzy分别为x,y方向施加的外部干扰力;x,y分别为x,y方向上的偏心位移。
2 离散时间无差拍控制电压生成
在离散时间系统控制理论中,无差拍控制是找出合适的输入信号,待其作用于系统后,在最少时间步长内使输出信号趋向于零。无差拍控制的最显著优点是数学推导严密、跟踪无超调、系统动态响应快、易于计算机执行。无差拍直接转矩控制方法的弊端是需要求解二次方程,不利于数字控制系统的实现。为了简化此方法,达到分离转矩、磁链控制电压的目的,在定子磁场定向的同步坐标系下,对电动机的模型进行分析,则有ψsq=0,ψsd=ψ1s。考虑到数字控制系统的采样时间比较小,在采样周期T内实现转矩与磁链的无差拍控制,需对(2)~(6)式进行离散化,得到
(11)
0=-R1si1sq(k)-ω1(k)ψ1sd(k)+u1sq(k) ,
(12)
(13)

(14)
Te(k)=np1ψ1sd(k)i1sq(k) 。
(15)

Δψs=ψ1sd(k+1)-ψ1sd(k)=
(16)
根据k时刻与k+1时刻的磁链误差,得到磁链控制的电压方程,即把(16)式代入(11)式可得
(17)
在直接转矩算法中,控制系统直接对电动机的转矩进行控制,对于稳定的系统,要求k+1时刻达到系统的负载转矩。
ΔTe=Te(k+1)-Te(k)。
(18)
根据(15)式可得
(19)
根据转矩误差得到转矩控制电压。把(19)式代入(18)式可得
(20)
把(12)~(14)式代入(20)式,消去i1sq(k+1)可得
(21)
(17)式和(21)式中的电压u1sd(k)和u1sq(k)即为k时刻实现SVM-DTC控制的定子电压。
3 基于离散时间无差拍的无轴承异步电动机SVM-DTC控制系统


图1 无轴承异步电动机控制系统框图

4 仿真和试验
利用Matlab中的Simulink工具箱,分别建立基于离散时间无差拍的SVM-DTC和传统DTC控制系统。仿真系统中采用的无轴承异步电动机参数如下:转矩绕组额定功率PN1=1 kW,额定转速nN=6 000 r/min,定子电阻R1s=2.01 Ω,转子电阻R1r=11.48 Ω,定、转子互感L1m=0.237 8 H,定子电感L1s=0.2424H,转子电感L1r= 0.2471H,极对数np1=2;悬浮控制绕组额定功率PN2=0.5 kW,定子电阻R2s=1.03 Ω,转子电阻R2r=0.075 Ω,定、转子互感L2m=0.009 3 H,定子电感L2s=0.012 H,转子电感L2r=0.014 7 H,极对数np2=3,电动机转子质量m=2.85 kg,转动惯量J=0.007 69 kg·m2。
对控制系统进行仿真,系统给定磁链为0.2 Wb,给定转速为6 000 r/min,转子x和y方向初始值都为200 μm。仿真时间为1 s,电动机启动时负载转矩为0,0.8 s加载2 N·m。
悬浮部分的稳定运行是无轴承异步电动机稳定运行的前提条件。图2a表明电动机可以实现稳定悬浮;图2b表明定子磁链圆波动很小;图2c为转速输出特性,转速为6 000 r/min,超调量小于0.2%,稳态误差小于5 r/min;图2d为转矩输出特性,可见电动机可以很好地跟踪负载转矩。
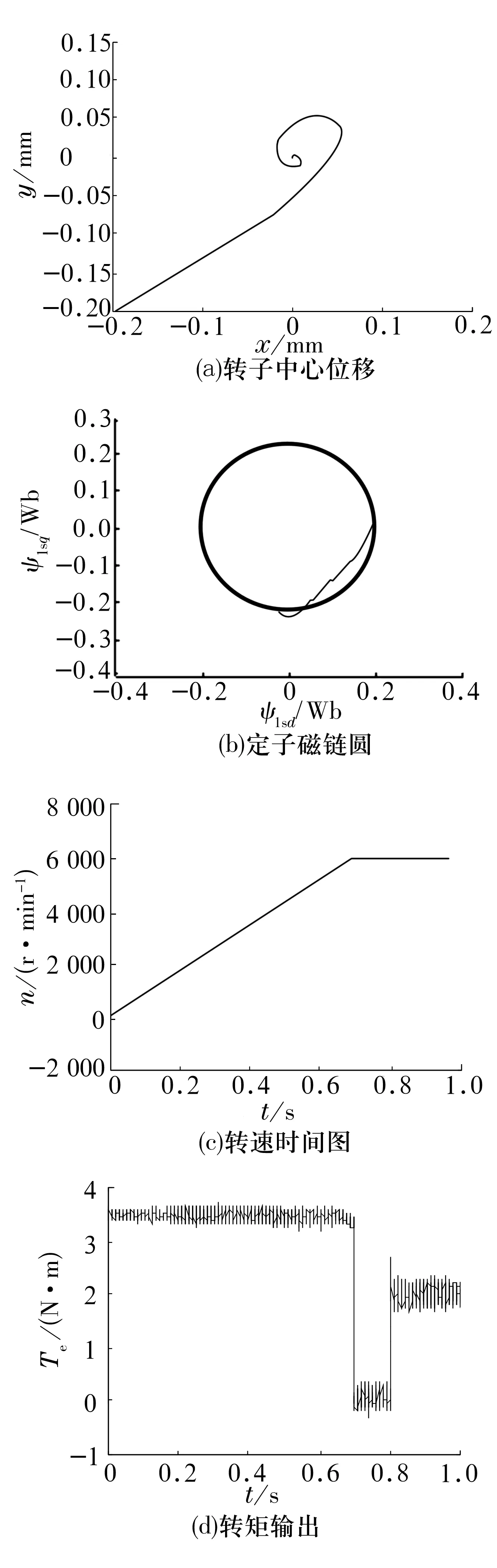
图2 控制系统仿真图
由图3~图5可知,基于离散时间无差拍的SVM-DTC方法与传统的DTC方法相比,定子磁链的脉动由0.025 Wb减小到0.008 Wb,转矩的脉动由2 N·m减小到0.3 N·m,x,y方向径向位移由0.12 mm减小到0.053 mm。
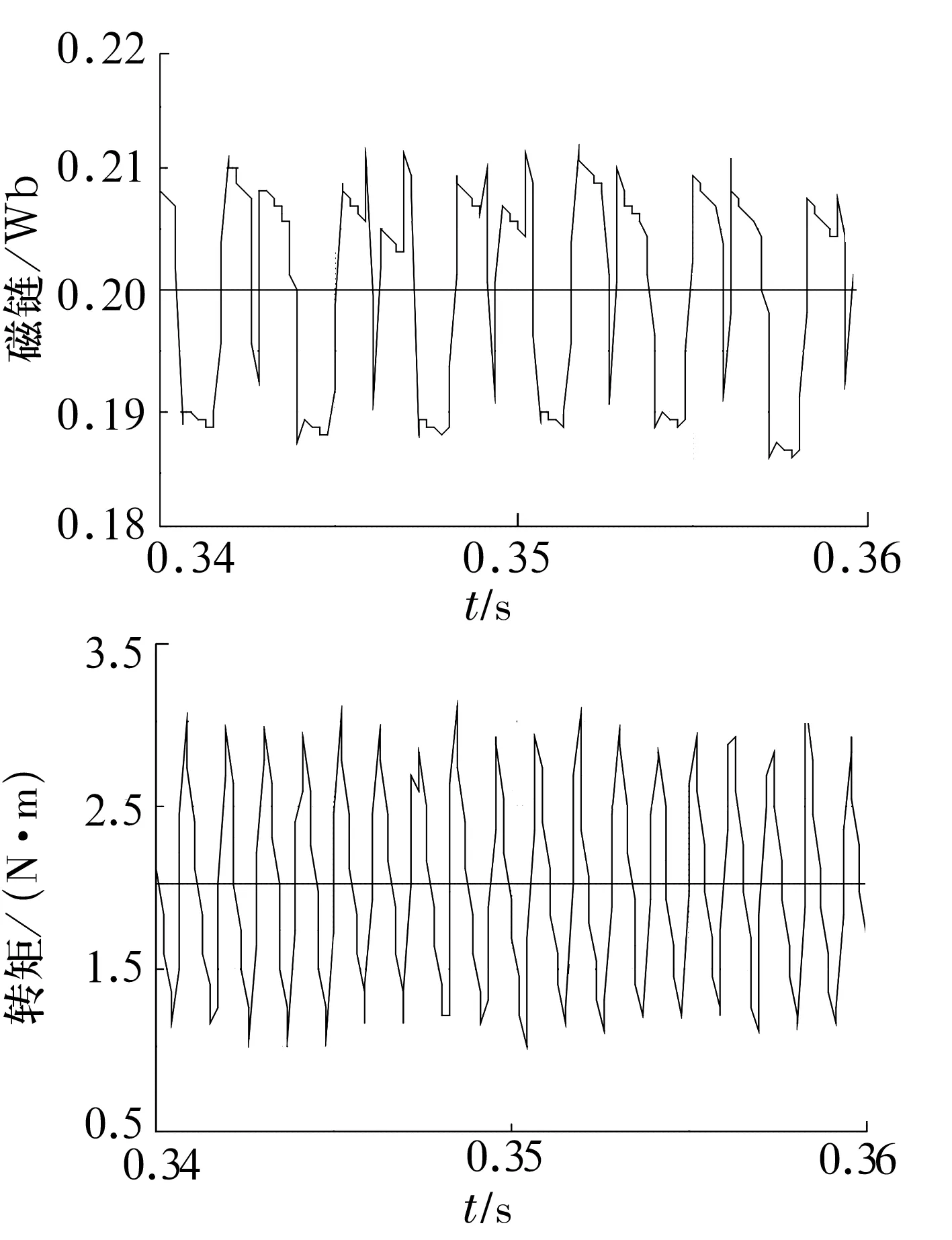
图3 传统DTC方法磁链与转矩波形(图中横线为给定值,曲线为实际值)
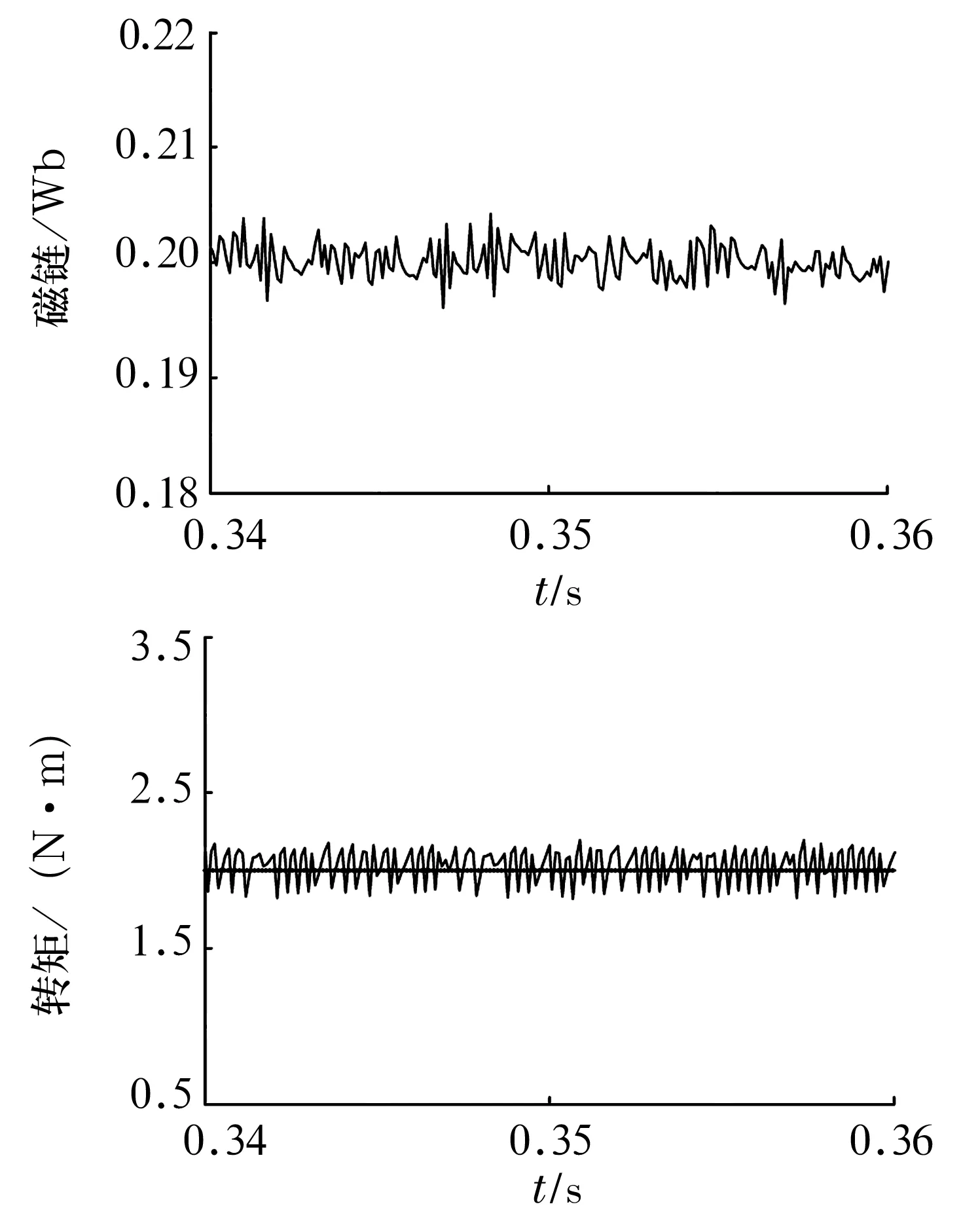
图4 基于离散时间无差拍的SVM-DTC方法磁链与转矩波形(图中横线为给定值,曲线为实际值)

图5 传统DTC和基于离散时间无差拍的SVM-DTC方法的转子的x,y方向位移
试验测试采用的无轴承异步电动机参数与仿真参数一样。选用TI公司的DSP2812控制器,核心算法为基于离散时间无差拍的SVM-DTC。当电动机达到2 000 r/min且稳定后,用示波器观测转子悬浮性能及两套绕组的电压及电流波形。
图6为转子径向位移波形,示波器每格为10μm,可见试验结果与仿真结果吻合,电动机可以实现稳定悬浮。

图6 x,y方向转子径向位移
图7a和图7b为转矩绕组的电压U1ab与电流i1a的波形,稳态时电动机转矩绕组输入的波形较好,电动机可以稳定地运行;图7c和图7d为悬浮控制绕组的电压U2ab与电流i2a波形,悬浮部分的电流波动较大,但基本符合正弦形状,说明其控制性能很好。

图7 转矩绕组与悬浮绕组电压、电流波形
5 结论
(1) 基于离散时间无差拍的SVM-DTC算法不仅可以实现转矩与磁链控制电压的动态解耦,而且解决了转矩环与磁链环的干扰问题,有利于控制参数的设定。控制电压由电压空间矢量脉宽调制实现,有助于转矩与磁链脉动的减小,并且使得逆变器具有固定的开关频率,有利于电力电子器件能力的充分应用。
(2) 与传统的DTC相比,这种改进的算法可以更好地抑制无轴承异步电动机转矩、磁链以及径向位移的脉动,从而提高了电动机的悬浮性能,有助于无轴承异步电动机的高速与稳定运行。
(3) 试验结果表明文中所提算法具有很好的鲁棒性,无轴承异步电动机可以实现稳定悬浮。
