Weibull随机寿命的统计量
2012-07-20王桂金
王桂金
(原钢铁研究总院,北京 100083)
1 疲劳寿命的Weibull分布
服从Weibull分布的疲劳寿命在可靠性理论中占有重要地位[1-2]。与其相关的实际疲劳寿命数据应该是一组满足Weibull分布的随机变量,并应给出Weibull分布定义的统计量。带量纲的统计量有均值即期望值μ, 方差σ2, 中值median和峰值mode。无量纲统计量有标准误差σ/μ,斜度γ1和过盈峭度γ2。对于具有形状参数κ和尺寸参数λ的二参数Weibull分布, 其计算公式为[1]

中值median=λ(ln2)1/κ,


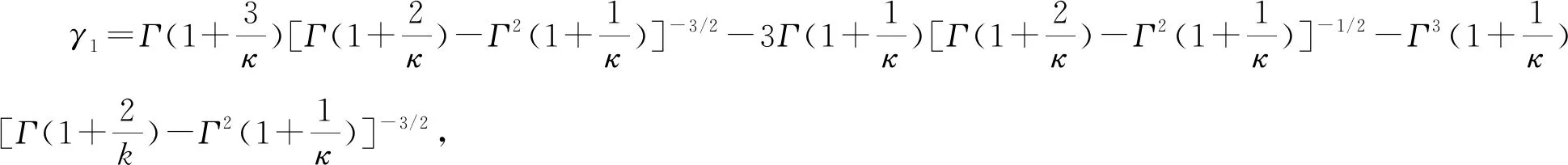
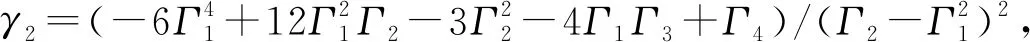
式中:Γi=Γ(1+i/κ),为Gamma函数;κ为形状参数;λ为尺寸参数。
值得注意的是,无量纲统计量都是形状参数κ的函数, 而与尺寸参数λ无关。 因此只要Weibull分布的形状参数相同,其标准误差、斜度和过盈峭度亦相同。通常研究者从试验数据出发,用极大似然法[1]或最大线性不变法[3]求出κ和λ,并计算拟合的可靠度。 由于在满足最小偏差的条件下,寿命分布形状不一定正确, 因此有必要从试验数据算出和分布形状有关的斜度γ1及过盈峭度γ2,并计算出对应的κ(γ1)及κ(γ2),再同拟合的κ值比较。为了避免实测寿命的系统误差和人为误差,可以首先随机产生一定数量的Weibull寿命(例如100个),按极大似然法计算κ和λ,并和设定值比较。然后由随机寿命数据按常规方法计算斜度和过盈峭度,进而推算相应的Weibull形状参数κ(γ1)及κ(γ2) ,并和极大似然法的形状参数κ相对照。最后还应该对实测寿命数据做同样的处理,以便对实际寿命数据是否为Weibull随机分布做出判断。
2 随机寿命和极大似然法拟合[1]
Weibull分布的随机寿命L为
L=λ(-lna)1/κ,
(1)
式中:a为在[0,1]区间内均匀分布的随机变量,为易于和铬钢轴承试验数据相比较,两者皆取为1。从文献[4]的附表中依次选取100个随机变量ai,i=1, 2, …,100,按(1)式算出的随机寿命Li见表1。根据下述极大似然法公式可求出这组数据的Weibull分布参数κ和λ

表1 Weibull随机寿命Li(i=1,2,…,100,κ=1,λ=1)

(2)
(3)
式中:N为所取样本大小,可根据需要选择,本例为10≤N≤100;Li为第i个试样的随机寿命。首先经对κ迭代计算使(3)式接近于零(小于|1×10-5|)得到κ(N),然后将其代入(2)式得到λ(N)。另外,按统计公式计算随机寿命分布的斜度γ1(N)和过盈峭度γ2(N),并计算出相应的形状参数κ(γ1,N) 和κ(γ2,N)。
3 计算结果
3.1 随机寿命分布的λ(N),κ(N),κ(γ1, N)和κ(γ2, N)
为检查随机寿命数据组的随机特性,计算了N=10~100 的λ(N),κ(N),κ(γ1,N)和κ(γ2,N),结果如图1所示(横坐标为样本大小N,下同)。当采用全部随机寿命数据,即N=100时,λ(100)=1.016 57,κ(100)=0.996 07,κ(γ1,100)和κ(γ2,100)分别为1.028 910和1.083 690,都很接近设定值1。结果表明这100个随机寿命符合κ=1和λ=1的Weibull分布,不仅偏差最小,而且分布具有κ=1的不对称性。极大似然法算出λ和κ在整个N范围变动不大,只在N<20时变动幅度略大。如果只取部分随机寿命计算斜度和过盈峭度及其形状参数和尺寸参数,则在N≥48时仍相当接近1。但是当N<48时,斜度和过盈峭度的形状参数显著增大,并且波动幅度大。 查表1可知,第48号是数据组的最大值 5.632 390,应该是它的出现终止了急剧的波动。因此,当随机寿命样本少于48时,虽然极大似然法能给出接近1的形状参数,但是分布不对称性未能达到κ=1的Weibull分布理论值。直到第48号数据加入,3种形状因子才得以一致。 其原因是极大似然法不涉及三、四次矩,对分布的形状不很敏感。

图1 随机寿命试样的极大似然法和由数据的斜度和过盈峭度得出的形状参数
3.2 随机寿命由小到大排列的λ(N),κ(N),κ(γ1,N)和κ(γ2, N)
通常实测寿命是由小到大按次序记录,为便于比较,把随机寿命由小到大排列,重新计算N=10~100的λ(N),κ(N)及κ(γ1,N),κ(γ2,N) ,结果如图2所示,可以看出:

图2 由小到大排列的随机寿命的极大似然法和直接由斜度及过盈峭度得出的形状参数
(1)与图 1相同, 全样本的随机寿命(即N=100),由极大似然法和由数据的斜度和过盈峭度等3种方法得出的λ值和各κ值均接近1 ,这是合理的;
(2)在10≤N≤100时,极大似然法得出的κ(N)由1逐步增大到1.671 50(N=21),随后稍微减小,再接着增大到2.822 30(N=10);
(3)从N=100到N=10由斜度推算的κ(γ1,N) 增长较快并有几个峰,例如在N=21达到峰值3.897 70, 在N=12处取极小值1.781 70,几乎和极大似然法的κ值1.743 30重合。这是极大似然法的κ(N)和由斜度推算的κ(γ1,N)第2次重合;
(4)由数据组的过盈峭度换算的κ(γ2,N)值,在所讨论的N范围相当离散。为清晰起见,在图上只标出κ(γ2,N)小于4.5 的值(其他图也作类似处理),不过仍然可以看到,在N=12,N=99和N=100处,κ(γ2,N)比较接近相应的κ(N);
(5)极大似然法的尺寸参数λ(N)从1.016 70(N=100)平稳地减小到0.056 83(N=10)。
4 试验分析
4.1 1208K+H208轴承的疲劳寿命[5](37个试样)
试验条件:载荷5 kN,转速 3 000 r/min,实测疲劳寿命见表2,计算结果如图3所示。图中:λ(37)=1 387 h,κ(37)= 0.955 50,κ(γ1, 37)=1.101 04,κ(γ2, 37)=1.149 38。
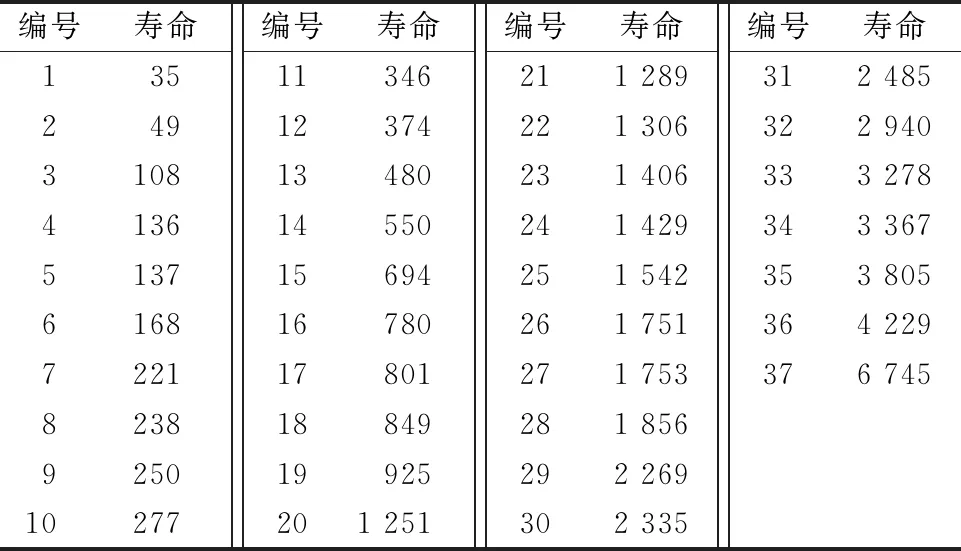
表2 H208轴承实测疲劳寿命(37个试样) h

图3 1208K+H208轴承实测疲劳寿命按极大似然法和按斜度及过盈峭度得出的λ(N) ,к(N),к(γ1, N)和к(γ2, N)
4.2 7208轴承的疲劳寿命[6](60个试样)
试验条件:径向载荷为8.281 kN, 轴向载荷为4.673 kN, 转速 4 500 r/min,结果如图4所示,λ(60)=267.12 h,κ(60)=1.024 43,κ(γ1, 60)=0.926 16,κ(γ2, 60)=0.931 83。

图4 7208轴承实测疲劳寿命按极大似然法和按斜度及过盈峭度得出的λ(N) ,κ(N),κ(γ1, N) 和κ(γ2, N)
4.3 6104轴承(50个试样)和6307轴承(20个试样)的疲劳寿命[7]
6104轴承试验条件:径向载荷 3.2 kN, 转速 2 800 r/min,结果如图5所示,λ(50)=125.28×106r,κ(50)=1.027 600,κ(γ1, 50)=1.336 360,κ(γ2, 50)=1.595 200。
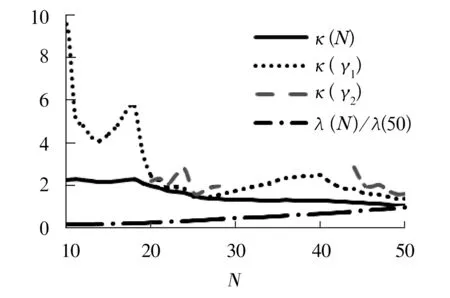
图5 6104轴承实测疲劳寿命按极大似然法和按斜度及过盈峭度得出的λ(N) ,κ(N),κ(γ1, N) 和κ(γ2, N)
6307轴承试验条件:径向载荷 7.8 kN, 转速 1 900 r/min,结果如图6所示。λ(20)=175.2×106r,κ(20)=1.577 70,κ(γ1, 20)=2.175。但κ(γ2,20)在κ=1~10时无解,因为γ2(20) =-0.725 960,低于γ2最小值-0.289(κ=3.42)。

图6 6307轴承实测疲劳寿命分布按极大似然法和直接由斜度及过盈峭度得出的λ(N) ,κ(N),κ(γ1, N) 和κ(γ2, N)
4.4 结果分析
总的看来,1208K+H208和7208轴承的实测疲劳寿命按极大似然法和直接由斜度及过盈峭度得出的各形状参数κ值在全样本处几乎重叠,与图2的结果很相近,因此其实测疲劳寿命分布十分接近随机分布。而6104和6307轴承的3种形状参数κ都还未完成相互靠拢的过程,可能需要更大的样本或者更严格控制样品制作和试验条件作进一步验证。因此认为,极大似然法、斜度和过盈峭度的形状参数κ相互重叠的出现,应是满足Weibull寿命随机特性的一个条件,具体而言,一组符合Weibull分布的疲劳寿命数据应有如下特征。
(1)当全样本的试样数N足够大,应在一个或一个以上的N值处,实测疲劳寿命按极大似然法和由斜度及过盈峭度得出的κ比较接近甚至重叠。这样,疲劳寿命分布和理想的Weibull分布既有最小的偏差, 而且分布的形状(即斜度和峭度)也一致。 如果有多个重合点,建议采用最大N值的形状参数κ和尺寸参数λ。
(2)随著N值增大,由于长寿命数据进入拟合计算,Weibull寿命分布的3种形状参数κ都逐渐变小。而最大似然法的尺寸参数则几乎呈线性增大。
(3)同一材料在同一试验条件下,如果有些试样因故不能试验到失效而提前舍去,可能会得出偏大的形状参数和偏小的尺寸参数,从而导致L10的偏差。
5 结束语
一般认为,最大似然法在大样本试验中比现有其他方法优越[1]。本研究表明,如果能辅之以数据的斜度和过盈峭度,取得有关寿命分布形状的信息,可以把Weibull分布参数评估得更合理。
