点缺陷深沟球轴承动力学特性的有限元分析
2012-07-20尹保健夏新涛高磊磊
尹保健,夏新涛,高磊磊
(河南科技大学 机电工程学院,河南 洛阳 471003)
球轴承具有极限转速高及噪声小等优点,广泛应用于航空航天、高速机床、精密仪表等领域中。随着传动系统向高可靠性、高速、静音方向的发展,对轴承的动力学接触特性和振动特性提出了越来越高的要求[1]。
计算机技术的迅速发展推动了有限元法在轴承分析中的应用,文献[2]采用静力学有限元法分析了圆柱滚子轴承的应力与应变,然而以往分析往往在静力和拟动力的条件下进行,随着机械产品向高性能要求方向发展,这样的分析结果很难满足设计需要。近年来轴承的显示动力学分析法越来越受到关注,文献[3]对滚动轴承运转过程进行了计算机模拟,讨论了滚动体接触应力的变化规律。文献[4]采用显示有限元方法模拟了滚动轴承次表面的裂纹及疲劳剥落。文献[5]建立了滚动体故障和麻点故障的有限元模型,对比分析了有、无故障轴承的不同特性。文献[6]建立了深沟球轴承的三维显示动力学模型,得出了轴承内圈、外圈、滚动体、保持架之间的接触应力、应变的变化情况,并将结果和Hertz理论结果进行比较,验证了动态有限元仿真的合理性。文献[1]综合考虑轴承径向载荷和转速的影响,对不同内圈转速下的滚动轴承进行仿真,得出了深沟球轴承运转过程的动态响应及球的应力分布。文献[7]通过选用塑性随动强化模型和双线性随动模型这两种不同的材料本构关系模型,计算了不同材料本构关系模型的低速轴承在两种情况下的应力状况。文献[8]分析了航空变速箱用滚动轴承表面缺陷对滚道接触应力、应变和接触角的影响。
本例采用双线性随动材料模型,以显示多体接触动力学为基础,在轴承外沟道六点钟方向加工不同直径的点缺陷,分析缺陷对轴承应力、应变的影响,总结不同直径点缺陷下内圈和钢球振动特性的演变过程,以期对轴承故障分析与诊断提供参考。
1 显示动力学理论基础
根据有限元法的离散思想得到动力学方程为
Mu″+Cu′+Ku=F(t),
(1)
式中:M,C,K分别为质量矩阵、阻力矩阵和刚度矩阵,对线性问题为常数矩阵,对非线性问题为函数矩阵;u″为加速度矢量;u′为速度矢量;F(t)为载荷矢量,是时间的函数。
在显示动力学中采用直接积分法中的中心差分法(显示算法中最有代表性、应用最广泛、最有效的方法)求解以上方程。加速度和速度可以用位移表示为
(2)
(3)
将(2)和(3)式代入(1)式可得各个离散点的时间点解的递推公式为
(4)
中心差分法是条件稳定的,稳定条件为
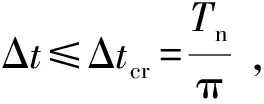
(5)
式中:Tn为求解系统的固有振动周期,总是大于系统中最小单元固有频率,因此网格的尺寸决定时间步长的选择,网格越小计算时间越长。
2 基于显示动力学的有限元模型
2.1 轴承的几何参数
表1给出了深沟球轴承6206的建模参数[9]及3个点缺陷直径。
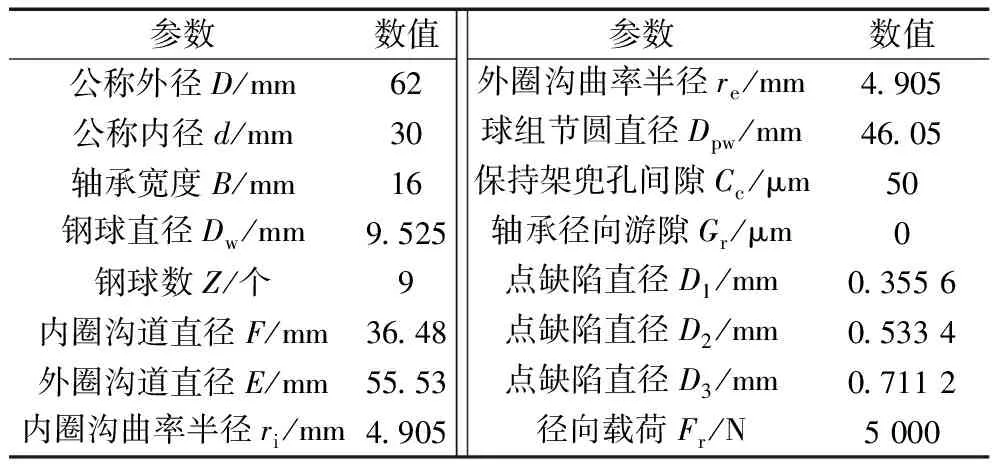
表1 轴承建模参数
2.2 材料的本构关系选择
主要研究缺陷处沟道应力与应变及钢球的动力学特征,所以选择轴承内圈和保持架为刚体,这样有利于轴承的加载和提高计算速度。钢球和外圈采用双线性随动材料模型,更符合材料的真实特性,有利于观察到塑性变形和残余应力等情况[10]。轴承内、外圈及钢球均采用GGr15钢,经过850 ℃淬火加热油冷+160 ℃回火2 h,热处理后屈服强度为1 617 MPa。泊松比υ=0.3,密度ρ=7.8×10-9t/mm3,弹性模量E=2.07×105MPa, 切线模量Et=E/100。保持架材料为黄铜,泊松比υ=0.324,密度ρ=8.545×10-9t/mm3,弹性模量E=1.06×105MPa。文中采用mmNs单位制,质量单位为吨,应力单位为MPa,分析时必须保持材料本构关系数据采用以上单位制系统。刚体元件的约束情况见表2。

表2 刚体元件约束明细表
2.3 网格划分与约束
在建立深沟球轴承有限元模型的过程中采用SOLID164三维实体单元,内、外圈采用面粘接映射网格划分法,在接触处加大网格密度。钢球通过切分的方法,采用映射网格划分法,这样有利于提高求解速度和精度。在点缺陷处采用自由网格划分法,在可能接触处加密网格。深沟球轴承满足对称分析的要求,所以取一半模型分析,在对称面加对称约束以提高计算速度。轴承在运转期间存在着三组接触,即内圈与钢球、外圈与钢球及保持架与钢球。内、外圈,保持架与钢球的静摩擦因数取0.17,动摩擦因数取0.005,接触类型均选择自动面面接触。工作中假定轴承内圈旋转,首先在内圈加载y向径向力Fr,等径向载荷稳定再加转动载荷ni,其值为1 730 r/min(181.17 rad/s),其加载(加速)曲线如图1、图2所示。外圈与轴承座过盈配合,所以约束轴承外圈与轴承座接触面的所有自由度[11]。
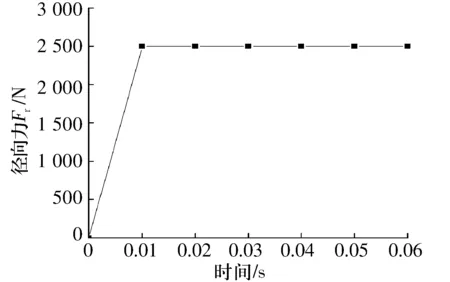
图1 径向力加载时间历程曲线
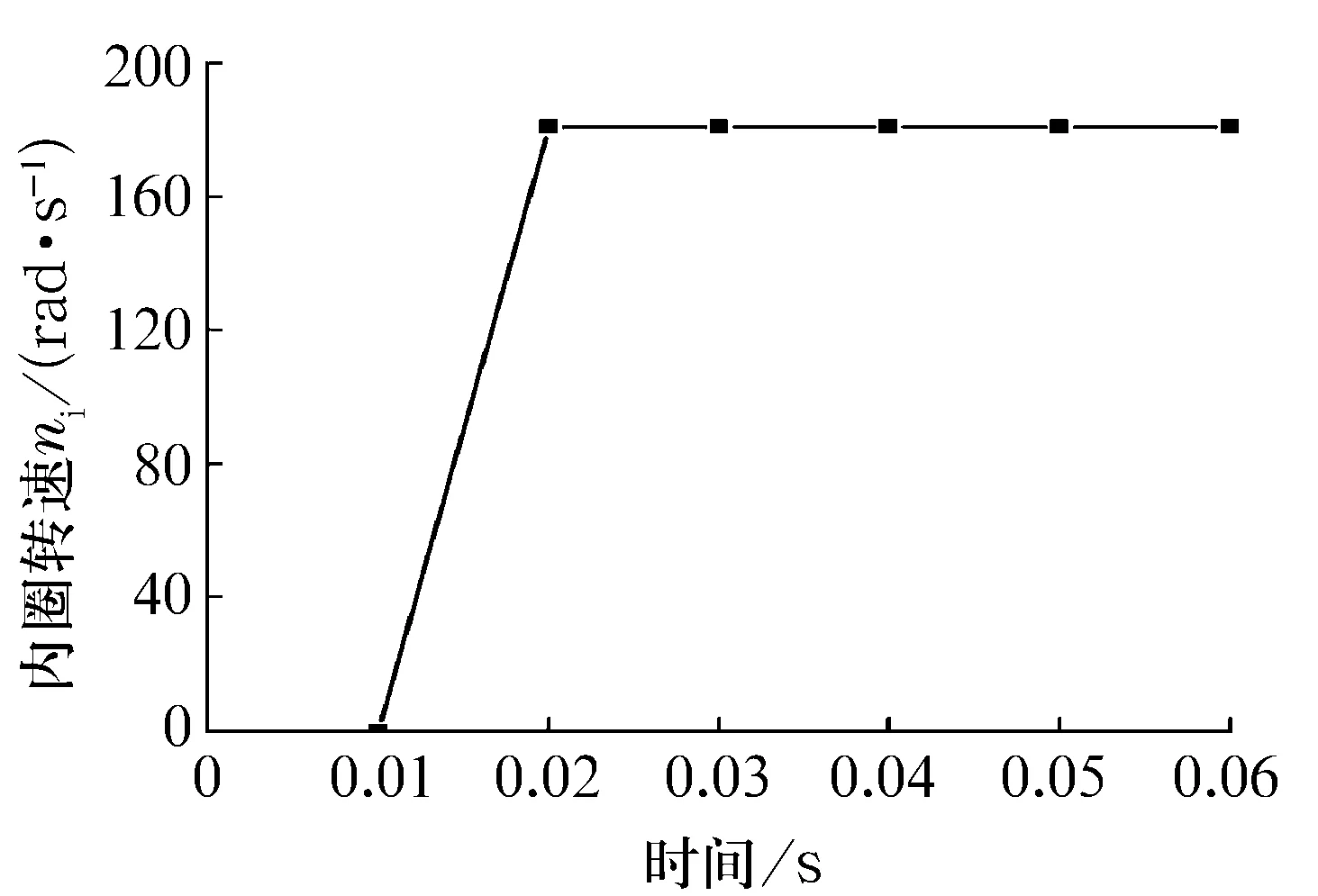
图2 内圈加速时间历程曲线
3 结果及讨论
3.1 正常轴承的有限元分析结果
深沟球轴承在径向载荷作用下,其载荷区为圆周的下半部,且最大承载钢球为最下方钢球。0.01 s内完成轴承的径向力加载,加载方式为线性加载,然后再加转动载荷。图3为轴承载荷区钢球接触应力云图;图4为承载钢球上单元接触应力时间历程。从图中可以看出,单元74 449属于最大承载钢球,单元101 449和64 324分别从属于最大承载钢球相邻钢球,有限元分析结果和理论计算载荷分布一致,且轴承加载过程中呈现典型的非线性特征。
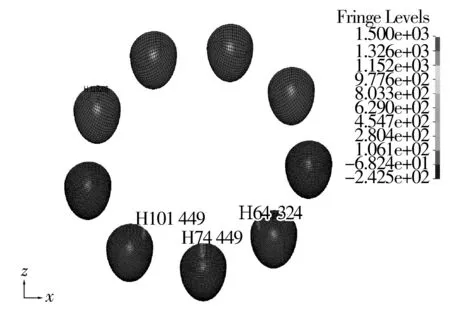
图3 轴承载荷区钢球接触应力云图
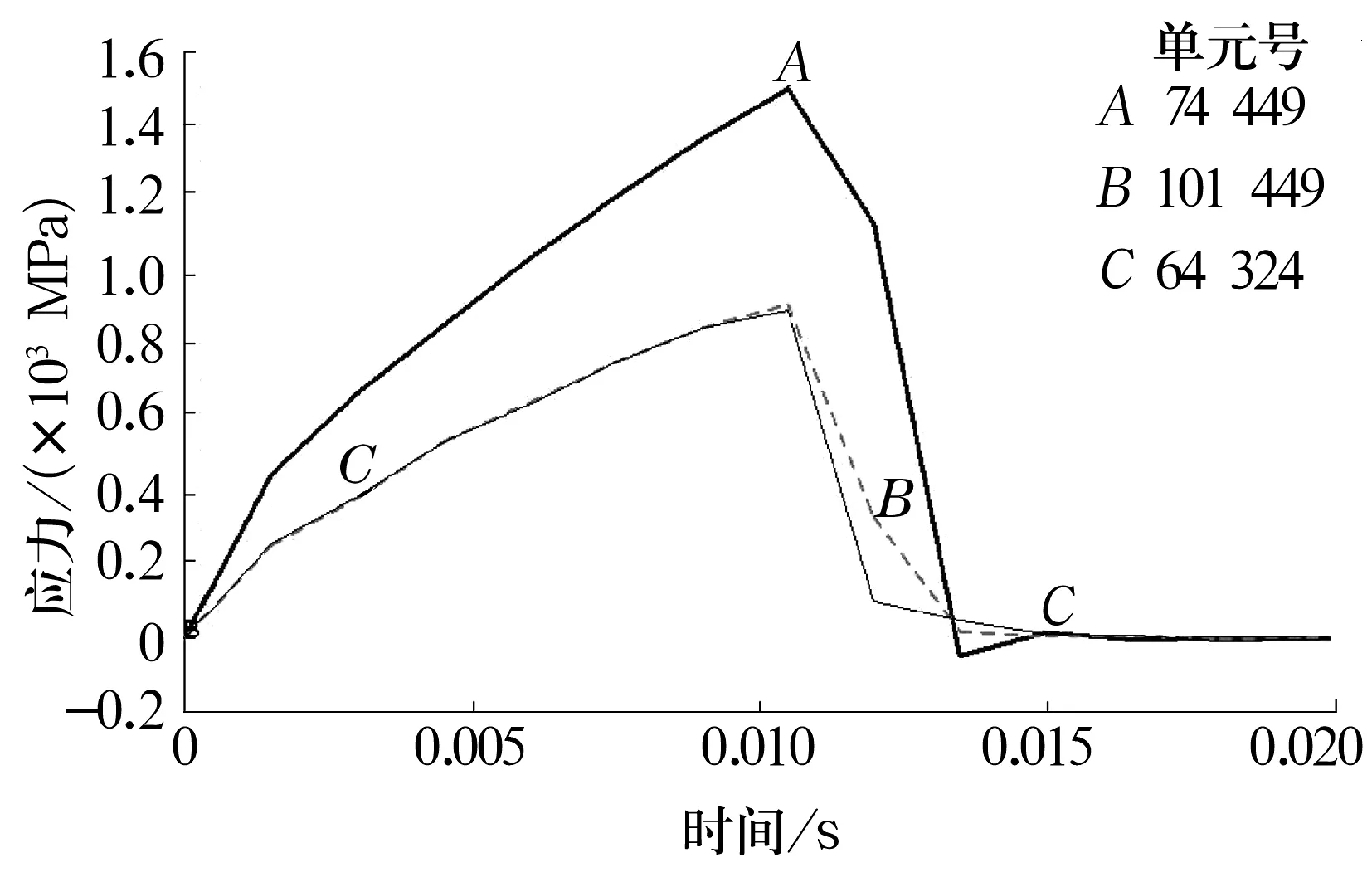
图4 单元接触应力时间历程图
依据圆周线速度原理分析轴承零件间的运动学特征,设钢球上A点和B点分别与轴承内、外圈接触,则A点速度等于内圈圆周线速度,B点速度等于外圈圆周线速度,因为外圈固定,所以vB=0。
(6)
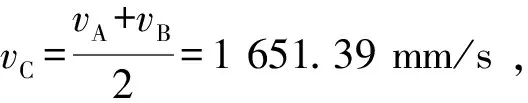
(7)
(8)
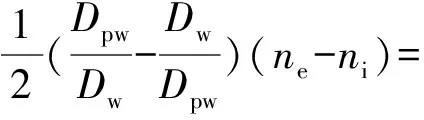
4 003.05 r/min,
(9)
式中:vC为钢球中心圆周线速度;nc为钢球公转速度;nw为钢球自转速度;ne为外圈转速;ni为内圈转速;wi为内圈角速度。
采用显示动力学分析轴承的动力学特征,取钢球上节点61 902绘制其速度时间历程,如图5所示。
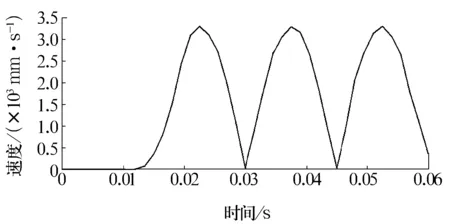
图5 钢球上节点61 902的速度时间历程图
从图5中可以得到节点61 902最大速度为3 317.11 mm/s,此时节点恰好与轴承内圈接触。0.03 s和0.045 s时节点与外圈接触,其速度为0。节点61 902经过0.015 s后再次与外圈接触,可求得钢球的自转速度为4 000 r/min,而由节点最大速度和最小速度可得公转速度为688.88 r/min。以正常轴承计算校核了所选用的各种接触参数、材料本构关系、算法及步长的合理性与可靠性,同时显示ANSYS/LS-DYNA软件是求解轴承动力学特征非常有效的工具,为分析点缺陷轴承的动力学特性奠定了基础。
3.2 点缺陷轴承运转过程中的应力分析
以深沟球轴承6206为例,在轴承外沟道六点钟处建立球冠特征的点缺陷,如图6所示,一半有限元模型如图7所示。
钢球通过点缺陷过程可以分为通过前瞬间、通过瞬间和通过后瞬间3个阶段,如图8~图10所示。
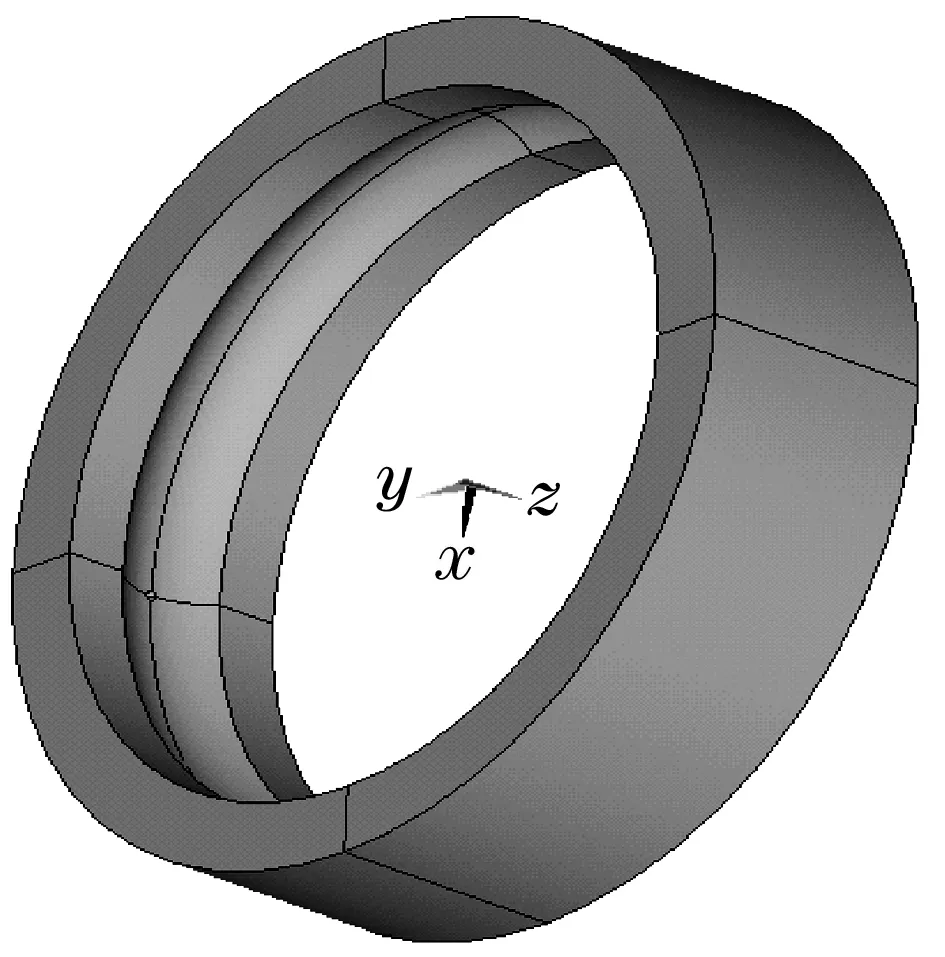
图6 点缺陷特征三维几何模型
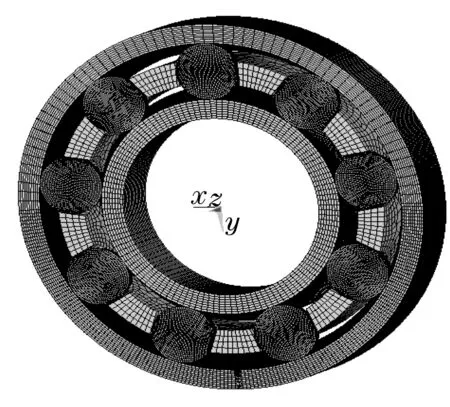
图7 有缺陷的深沟球轴承有限元模型

图8 通过缺陷前瞬间
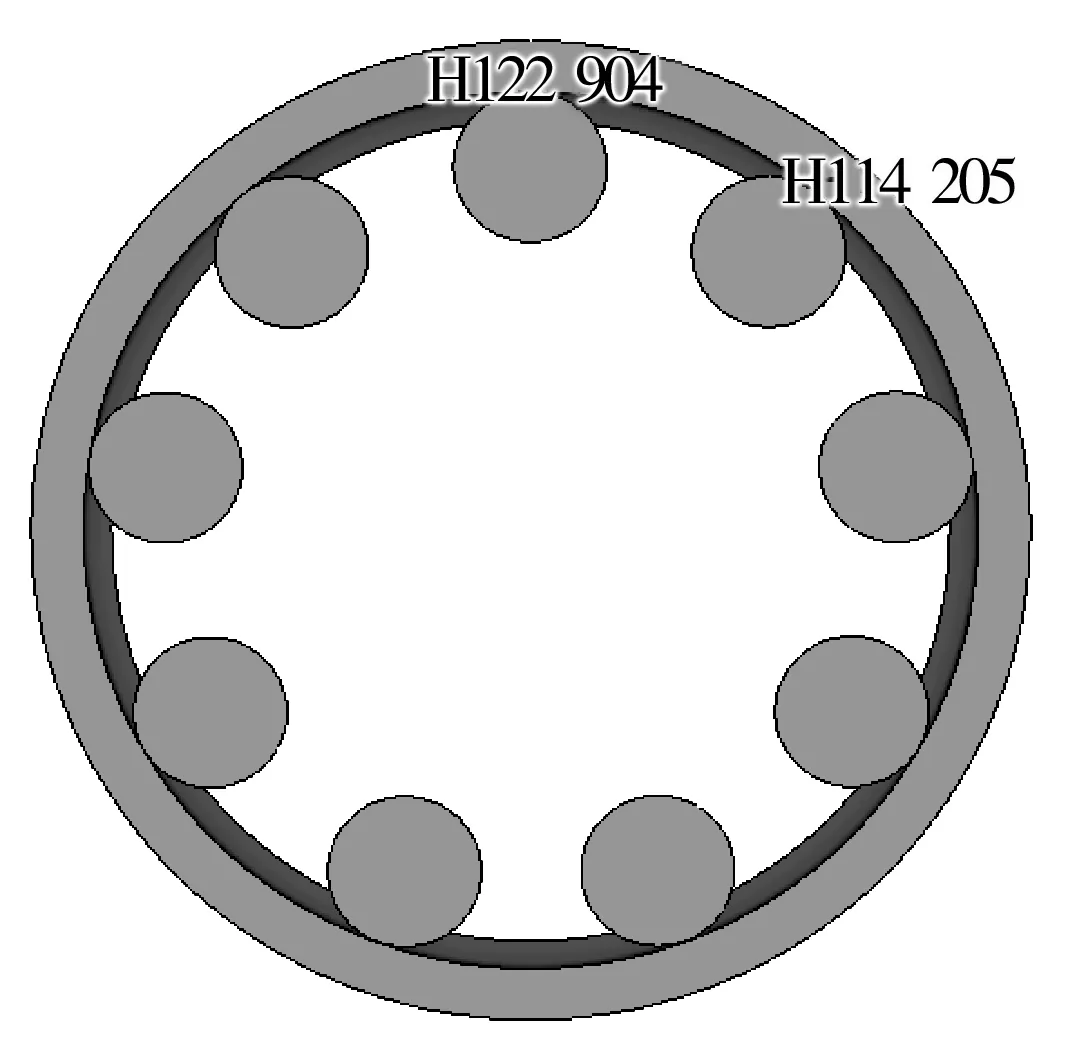
图9 通过缺陷瞬间

图10 通过缺陷后瞬间
在轴承运转过程中捕捉3个阶段的瞬间应力图,分别选取钢球与外沟道接触处最大接触应力单元151 437,122 904和184 418,绘制3个单元的接触应力时间历程曲线(图11)。当钢球通过缺陷瞬间,相邻钢球所承担的接触应力突然增加。图12为单元122 904和114 205的接触应力时间历程曲线。
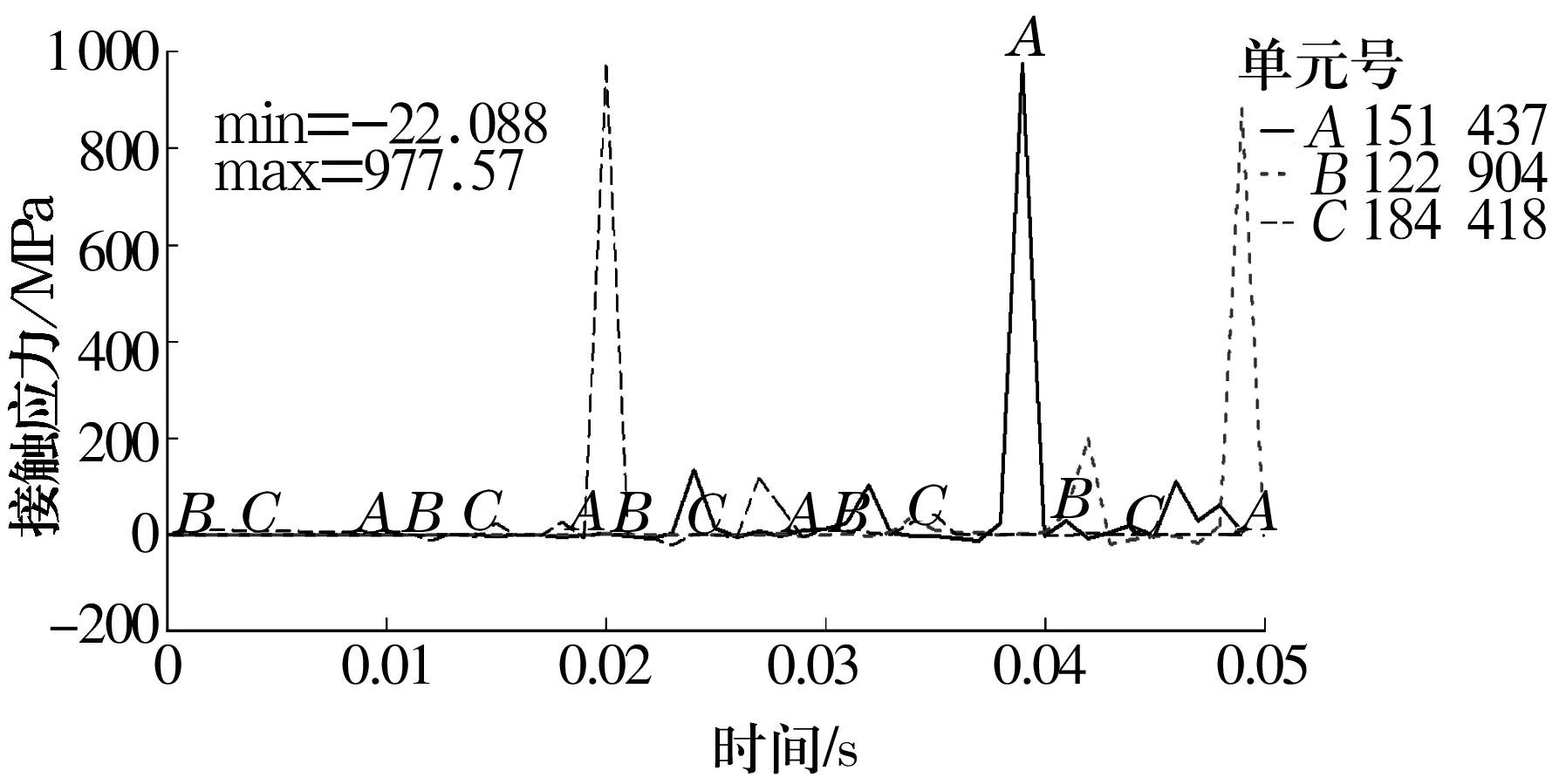
图11 单元151 437,122 904和184 418接触应力曲线图
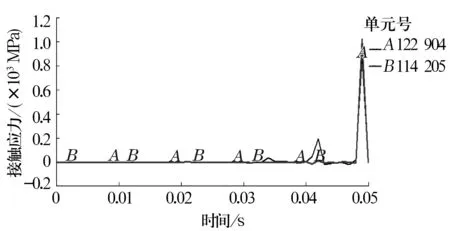
图12 单元122 904和114 205的接触应力曲线图
从图11可以得出钢球通过缺陷过程中,钢球最大接触应力值经历了大-小-大的过程[12],这恰恰与正常轴承最大接触应力小-大-小的变化过程相反。综合以上情况,钢球在通过缺陷前后应力会突然变大,在通过缺陷瞬间相邻钢球承载也会突然增大,缺陷的存在打破了轴承正常的载荷分布,造成了振动与冲击。图13为钢球通过瞬间缺陷处的Mises应力云图,这时外圈Mises应力值为轴承运转过程中的最大值。图14为钢球通过瞬间缺陷处Mises应力云图,Mises应力最大值分布在点缺陷圆周接触处。所以外圈的破坏首先在缺陷处且缺陷直径将扩大,磨粒将造成沟道或钢球表面新的划伤,随后扩展为新的点缺陷,造成轴承失效。
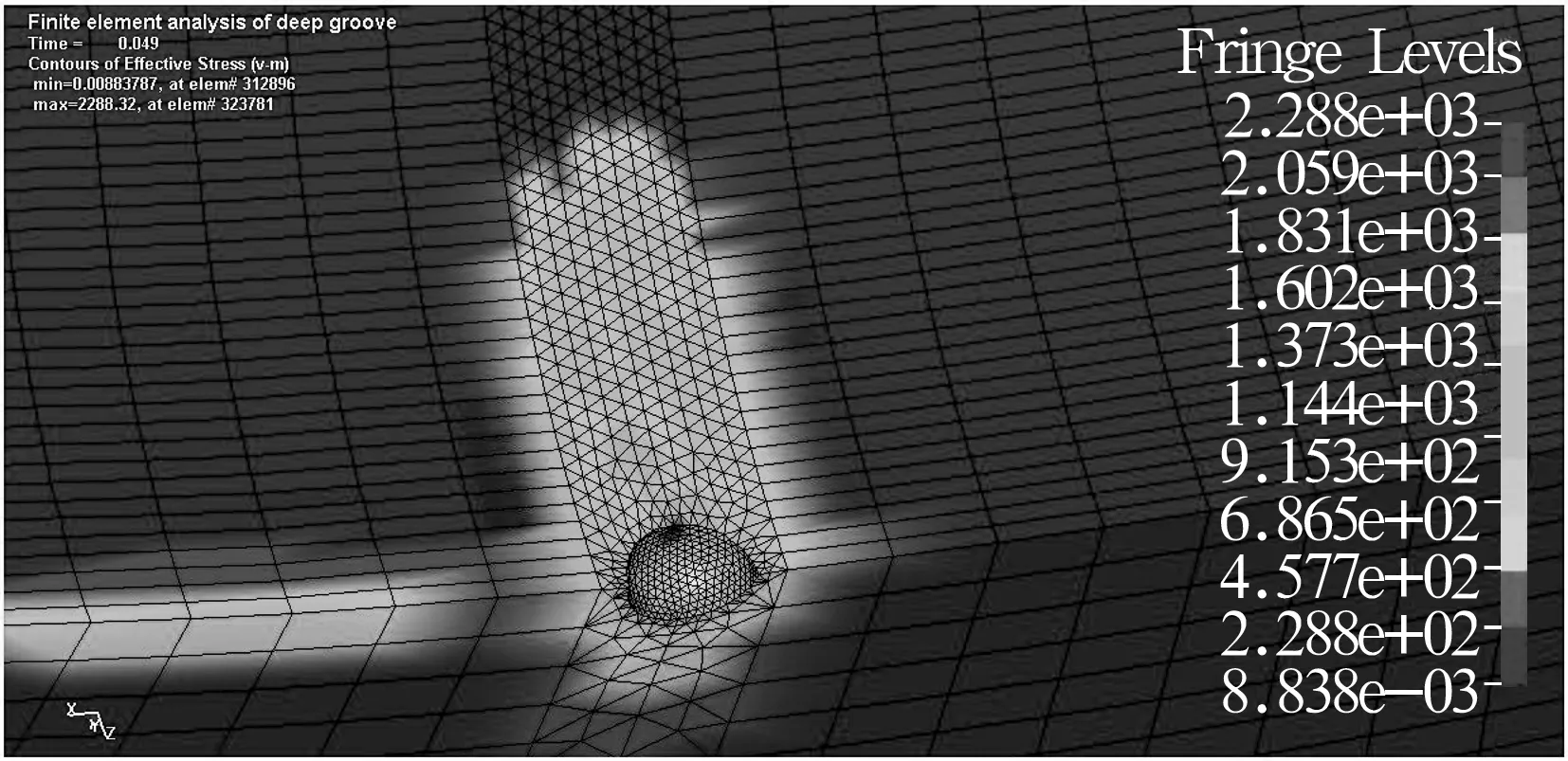
图13 钢球通过缺陷瞬间缺陷处Mises应力分布云图

图14 钢球通过瞬间缺陷处Mises
3.3 点缺陷轴承运动过程中的振动特性分析
为了更准确分析缺陷轴承的振动特性,需要减少求解时间,增加结果文件输出步数。因此在0.003 s即完成径向载荷Fr/2的加载,之后对内圈施加旋转载荷至0.005 s完成。求解总时间为0.025 s,结果文件输出步为100。分别建立表1所示的3种不同直径的点缺陷特征,分析在3种直径下x方向内圈的加速度随时间历程变化曲线。3种情况下内圈某节点处加速度随时间变化历程曲线如图15~图17所示。
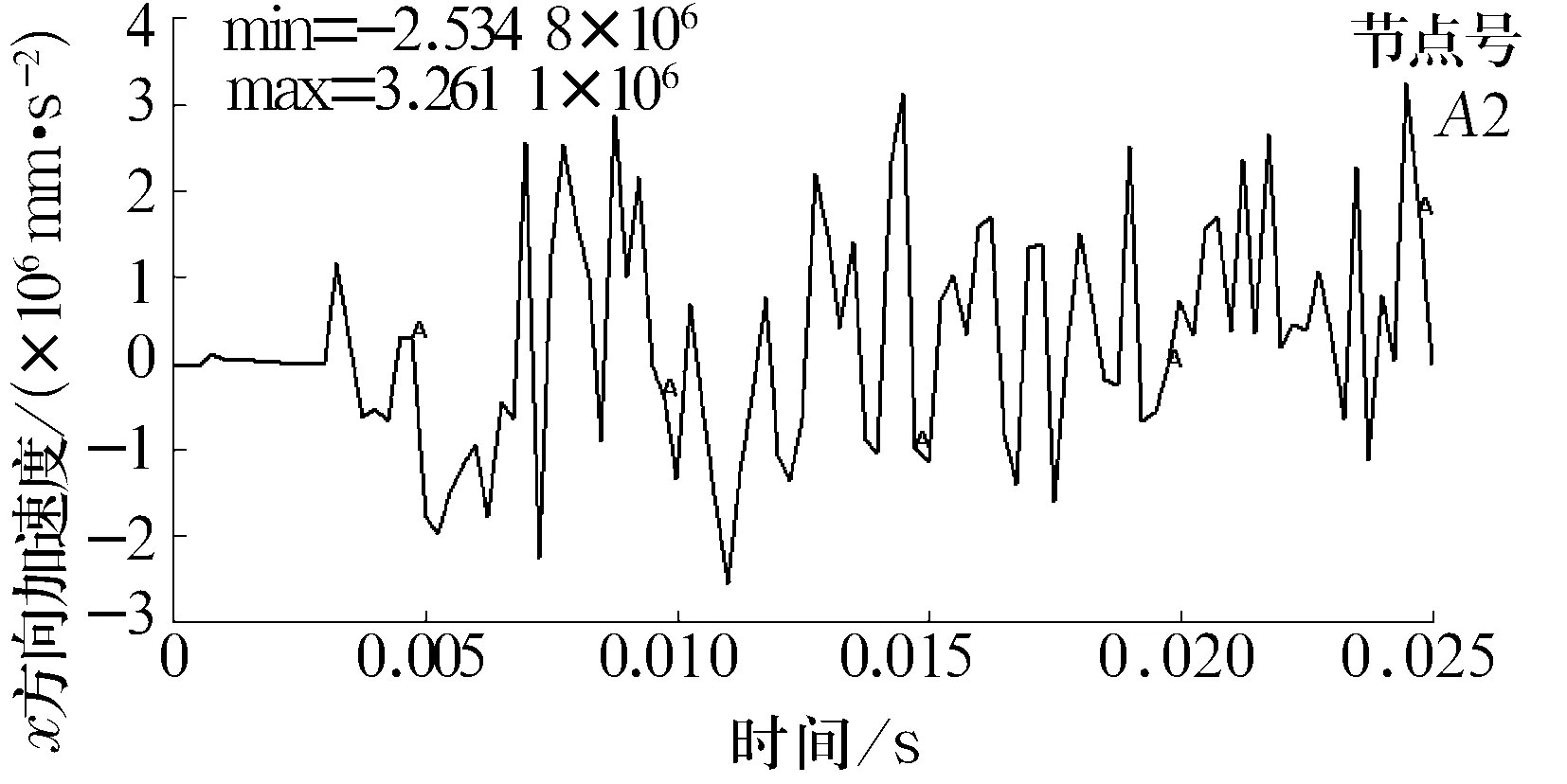
图15 缺陷直径为0.355 6时内圈节点2 x方向加速度
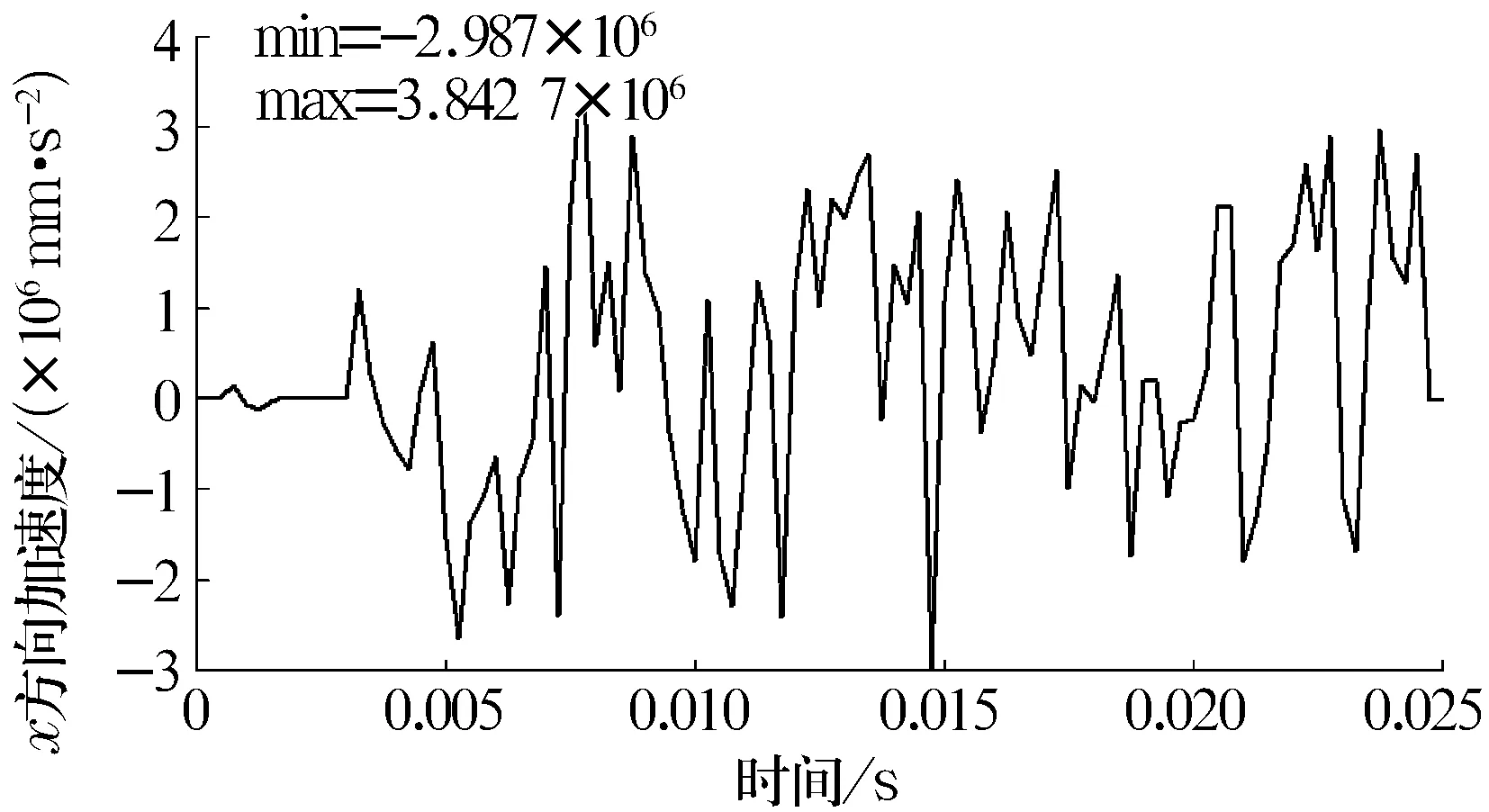
图16 缺陷直径为0.533 4时内圈节点2 x方向加速度
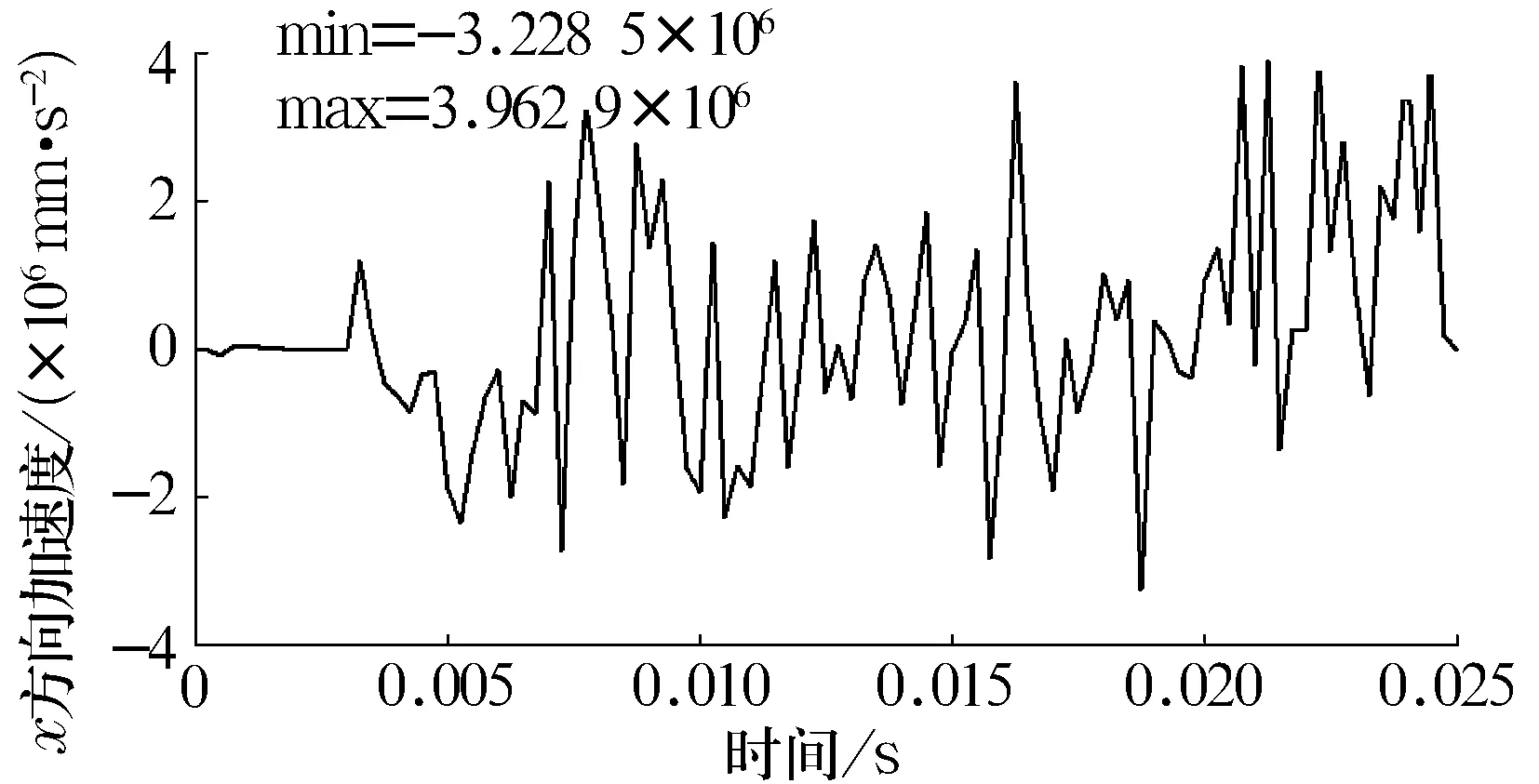
图17 缺陷直径为0.711 2时内圈节点2 x方向加速度
为了研究钢球在运转过程中的振动特征,取钢球上相同的节点171 922观察其在3种不同直径缺陷下的加速度时间历程曲线,其加速度时间历程曲线如图18~图20所示。
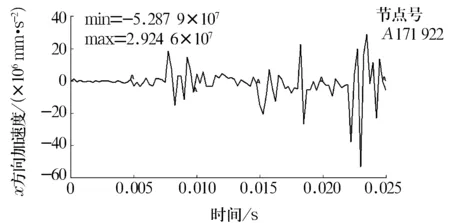
图18 缺陷直径为0.355 6时钢球上节点171 922 x方向
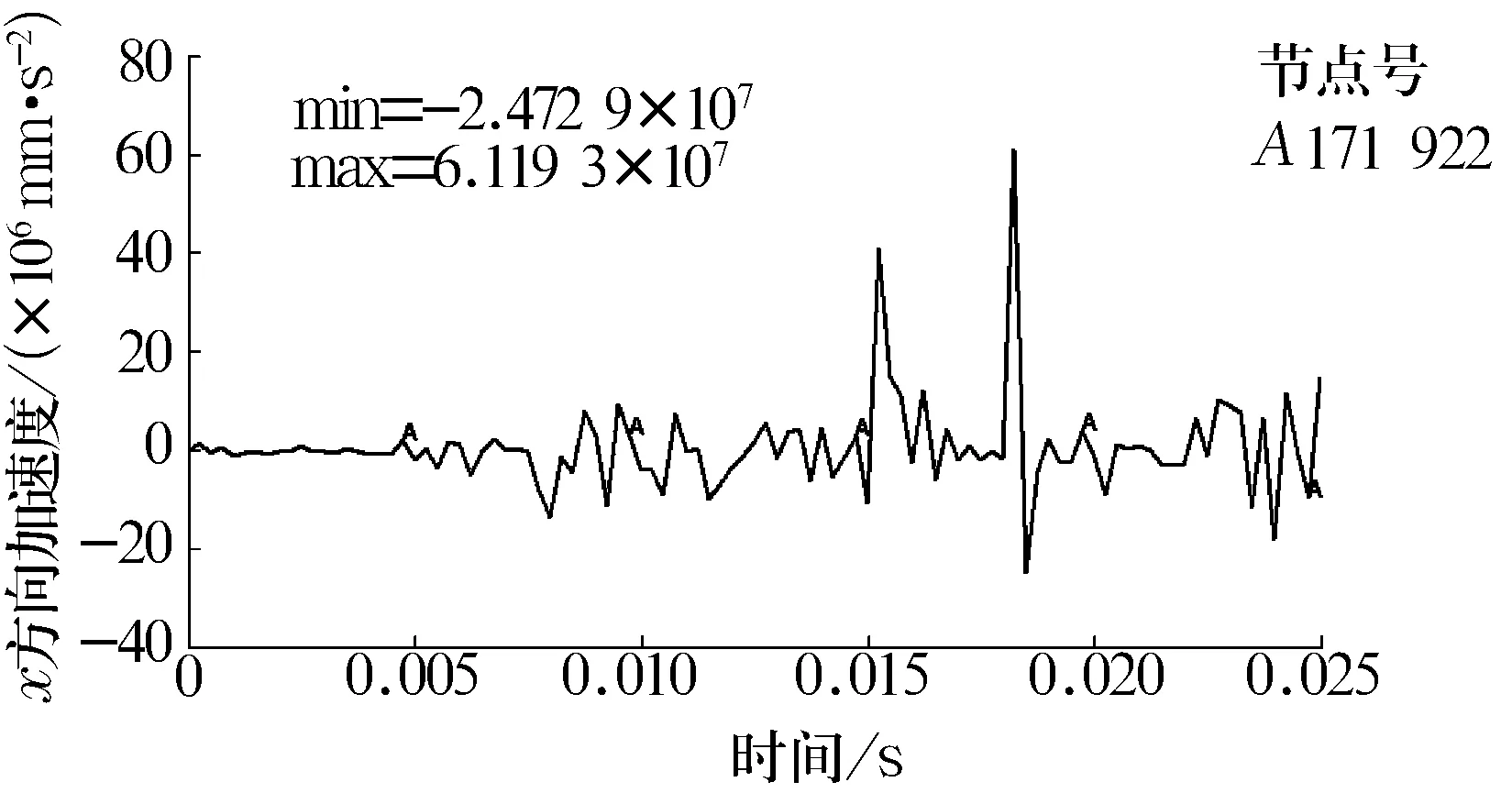
图19 缺陷直径为0.533 4时钢球上节点171 922 x方向
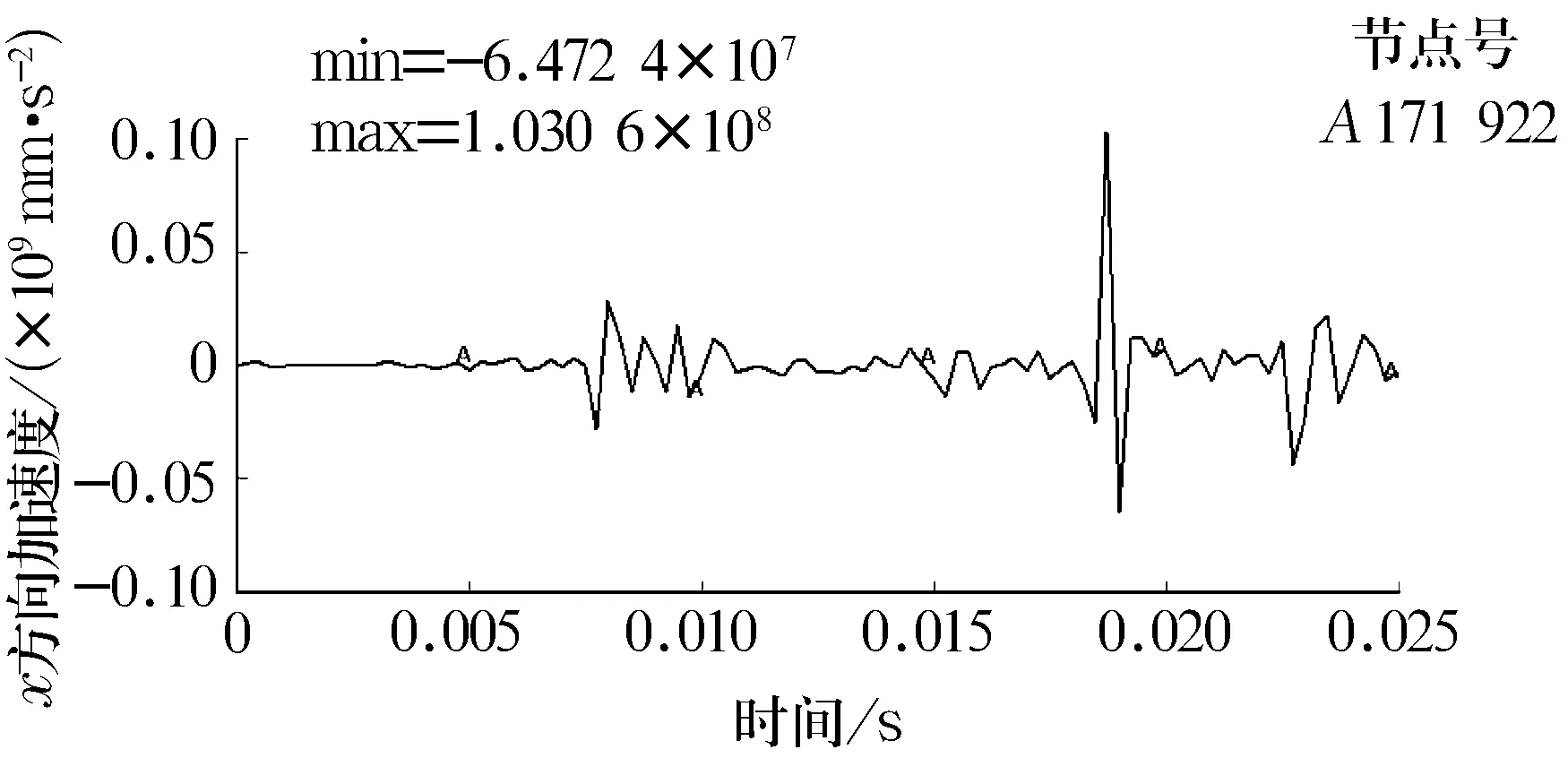
图20 缺陷直径为0.711 2时钢球上节点171 922 x方向
分析以上曲线可知,随着缺陷直径的增大,内圈和钢球的振动均不断增强且钢球的振动要大于内圈。轴承振动特性的恶化将造成噪声激增。
4 结论
(1)通过对无缺陷球轴承的显示动力学仿真结果与理论计算结果的对比,说明显示动力学软件对研究轴承的运动学特性是十分合适和有效的,且直观形象。
(2)外圈存在点缺陷时,外圈的最大Mises应力出现在缺陷的圆周部位,其原因主要为形状畸变造成了应力集中,从而导致此处更容易形成新的疲劳剥落,划伤钢球或沟道表面造成新的点缺陷。
(3)通过对3种不同直径点缺陷深沟球轴承的显示动力学分析得出:随着点缺陷直径的增大,轴承内圈和钢球的振动特性均不断恶化,导致轴承噪声和温升增大,进而使轴承产生功能性失效。
