基于神经网络的液体动压润滑固定瓦推力轴承优化设计

高朝祥，王充，任小鸿，周文

(四川化工职业技术学院，四川 泸州 646005)

1 概述

液体动压润滑推力轴承是应用液体润滑承载原理的机械结构部件。固定瓦推力轴承为液体动压润滑推力轴承中的一种，其瓦块固定在基体上，利用轴颈本身高速回转将润滑油带入摩擦对偶面间产生油楔，形成压力油膜把摩擦对偶面分开。其主要应用于工况比较稳定的场合，如水轮发电机、汽轮机等，承受轴向载荷。如果两摩擦对偶面平行，转动中润滑油将被挤出，不易形成动压油膜。为了压力油膜的形成和改善滑动摩擦，轴瓦沿圆周方向被分隔成具有一定斜度的若干固定瓦块，并与基体形成一个整体，如图1所示。合理的轴瓦面结构能使推力轴承具有良好的润滑性和承载能力等，不易产生咬合现象。文中对轴瓦面结构建立优化的数学模型，利用神经网络算法对其进行优化设计。

图1 固定瓦推力轴承

2 数学模型的建立

为了确保液体动压润滑固定瓦推力轴承处于稳定的液体润滑工作状态，轴承设计需要考虑自身几何形状、润滑油的性能和载荷特性等。

2.1 选取设计变量

如图2所示，影响轴承的参数包括：轴承内径D1(m)、轴承外径D2(m)、轴承宽度B(m)、轴瓦块数z、轴瓦出口油膜厚度h1(m)、轴瓦入口油膜厚度h2(m)，油膜厚度比δ、润滑油动力黏度η(Pa·s)、轴承转速n(r/min)、轴瓦承载面长度L0(m)、承载瓦块在以轴承平均直径Dm为直径的圆周上的弧线长度Lb和La[1]。在一定的工作载荷和转速下，为提高轴承工作时承载能力和使用性能，这里选取以下几个参数：B，L0，h1，h2，η，D2作为设计变量。 因此，优化设计变量为X=(x1,x2,x3,x4,x5,x6)T=(B,L0,h1,h2,η,D2)T。

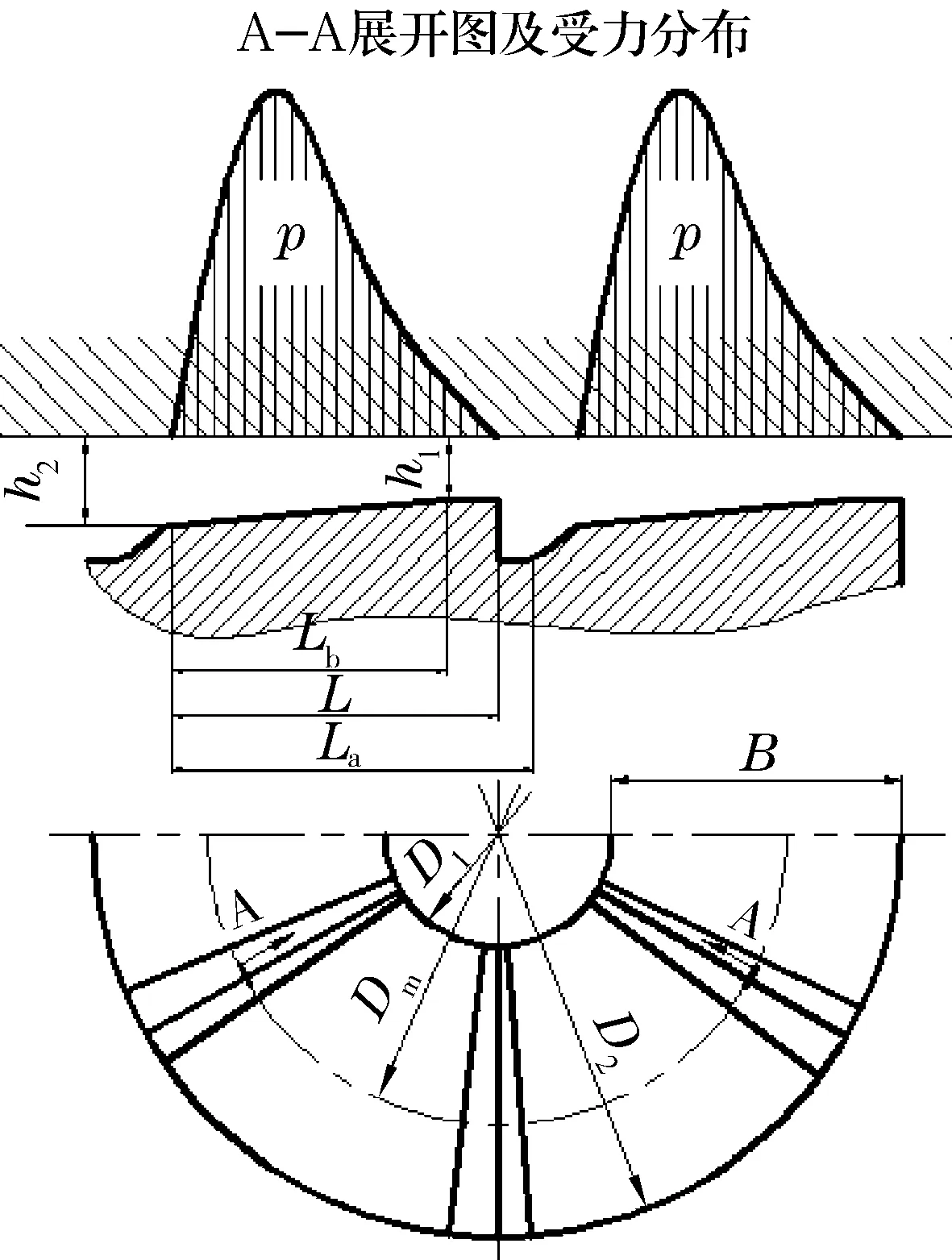
图2 固定瓦推力轴承的几何尺寸及受力分布

2.2 目标函数的建立

(1)

(2)

(3)

式中：v为轴颈圆周速度，m/s;p为轴承所受平均压强，MPa；F为轴承所受外力，N；轴承宽度B=(D2-D1)/2；轴瓦块数z一般为6～12块；轴承平均直径Dm=(D1+D2)/2[4]。

把(2)～(3)式代入(1)式得

(4)

代入设计参数，则目标函数表示为：

f(X)=f(x1,x2,x3,x4,x5,x6)=

(5)

2.3 约束条件

由图2可知，πDm=zLa。轴承填充系数kz=L0/La，一般kz=0.7～0.85，取kz=0.75,则Dm=zL0/(0.75π)，L0=0.75π(D2-B)/z。轴颈转速n已知，轴瓦使用材料性能指标可通过资料查找选定。

2.3.1 轴承几何尺寸

轴承内径D1稍大于轴颈直径d[4]，假定取大于2 mm。则

g1(X)=2x1+d+0.002-x6≤0。

(6)

2.3.2 轴承的平均压强

瓦面许用平均压强[p]一般低于1.5～3.5 MPa，取[p]=2.5 MPa。 则

(7)

2.3.3pv值

为了防止轴承出现胶合，不仅应该限制轴承的温升，还应使轴承的pv小于允许值[5]，

(8)

2.3.4 油膜厚度比

油膜厚度比δ=h2/h1=1.8～3[4],即：1.8≤x4/x3≤3,则

g4(X)=1.8-x4/x3≤0；

(9)

g5(X)=x4/x3-3≤0。

(10)

2.3.5 温度限制

轴承工作时，轴承的润滑油温升也是在设计中必须考虑的一个重要因素，

qv≈0.7Bh1vz。

对于L0/B=0.5～1.3,h2/h1=1.8～3的推力轴承，

合并上述各式，代入设计变量，整理得

一般入口温度t2=30～45 ℃，依不同润滑方式而定，出口温度t1不超过100 ℃，即t2+Δt≤100，则

g6(x)=30+Δt-100≤0。

(11)

2.3.6 动力黏度

为了保证润滑效果，轴承使用润滑油动力黏度应大于最小许用黏度ηmin，即η≥ηmin，则

g7(X)=ηmin-x5≤0。

(12)

综上所述，固定瓦推力轴承优化设计的数学模型[6]为

(13)

3 神经网络算法理论和方法

神经网络算法理论是模拟生物神经系统单元，按一定的拓扑关系连接形成一个高度复杂的非线性动力系统，通过学习机制趋于稳定，收敛到渐近平衡稳定点，这个平衡稳定点为能量函数的极小点。系统的能量函数与优化问题的目标函数相对应，人工神经网络的各个参数与优化问题的各个设计变量相对应，神经网络系统的演化过程在优化问题的解空间与寻优过程相对应[3]。

对于有约束的优化问题，即

(14)

利用外点罚函数法，可写成求下面函数的极小点

(15)

式中：f(X)为目标函数；r1,r2为惩罚因子；hv(X),max{0,gi(X)}为罚函数。

(16)

BP算法通过调整阈值和连接权系数值使得输入的xk的能量函数Ek达到最小，

(17)

对所有输入样本xk(k=1,2,…,N0)，使

(18)

达到最小。

采用梯度下降法求解这类优化问题，迭代公式为

(19)

(20)

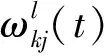
4 算例

已知某汽轮机F=20 kN，n=1 200 r/min，d=50 mm，z=6，[p]=2.5 MPa，[pv]=85 MPa·m/s，ρ=900 kg/m3,ηmin=0.016 Pa·s,αb=50 W/(m2·℃),cp=2 000 J/(kg·℃)，试设计此轴承。

根据固定瓦推力轴承编制BP算法Matlab程序[8]进行计算。神经网络优化初始值：X0=[0.01,0.01,0.000 005,0.000 005,0.01,0.1]，其优化结果与常规设计结果对比见表1。

表1 常规设计解与神经网络优化解

常规设计方法常用试算的方法，计算工作量大，查表、查图误差大。神经网络优化算法从初始点向最优化解逼近，具有较好的全局搜索能力。由表1可知，神经网络优化算法较常规设计能更准确找到固定瓦推力轴承各参数的最优解。

5 结束语

利用上述液体动压润滑固定瓦推力轴承的设计分析，结合人工神经网络的最新进展和BP算法解决最优化问题时，使待优化问题的目标函数对应于某个网络的能量函数。当网络趋于稳定时，目标函数能稳定地收敛至极小点。但也存在网络参数选择不好的缺陷，而得不到最优化解，有待改进神经网络方法对其进一步研究。算例结果表明，这种优化设计方法具有较好的稳定性，在解决液体动压润滑固定瓦推力轴承优化问题方面是有效的。