椭圆轴承椭圆度对转子稳定性的影响

张艾萍, 林圣强，李雨娇

(东北电力大学，吉林 吉林 132012)

随着大型旋转机械的发展，圆柱轴承已经无法满足现代机械对稳定性的要求，现代电厂汽轮发电机轴承很多都是采用椭圆轴承，因为在实际汽轮机组运行中，椭圆轴承比圆柱轴承更具有安全性，不易发生油膜振荡和油膜失稳的现象，可更好地保证转子运行的可靠性和机组的稳定性。目前国内还不能给出椭圆轴承的实际油膜特性，这对分析椭圆轴承和转子的稳定性很不利。

国内许多学者通过解Reynolds方程来研究滑动轴承的特性，其实Reynolds方程只分析了油楔的形成[1]，却忽略了黏性流体的一个重要特性——有漩性[2]，故不能真实反映轴承的实际油膜润滑情况。如文献[3-4]采用几种不同方法求解Reynolds方程，分析不同椭圆度对转子稳定性的影响，但没有给出椭圆轴承的实际油膜压力分布，且在计算Reynolds方程时未考虑进油口压力对轴承油膜的影响、剪切力对油膜力的影响、漩涡及湍流等，故误差较大。而通过黏性流体动量平衡方程(N-S方程)计算椭圆轴承油膜特性，能较可靠地反映油膜的实际特性。文献[5-6]用N-S方程计算了圆柱轴承的油膜特性，但没有给出油膜特性对轴承和转子稳定性的影响。随着计算流体动力学(CFD)仿真技术的发展，在狭小和细长的空间内也可以画出高质量的网格，且不会忽略边缘细节。特别是在计算漩涡方面有很大进展，Shear Stress Transport(SST)模型可以很有效地考虑到狭小通道的剪切应力，且不会过分估算漩涡的强度，比较符合轴承与轴颈狭小空间内的流动。下文从数值模拟出发，通过计算N-S方程来研究椭圆轴承的油膜特性，考虑到温度对油膜的影响，采用温度压力耦合计算，并结合转子稳定性，具体分析不同椭圆度(相对侧隙/相对顶隙)对转子稳定性的影响。

1 物理模型

计算的椭圆轴承物理模型如图1所示。图1a为用三维制图软件UG建立的椭圆轴承的物理模型；因为轴承与轴颈间隙很小，基本看不出与圆柱轴承的差别，夸大实际建立的物理模型如图1b所示。其中，偏心率ε=0.5，最小油膜厚度为0.03 mm，汽轮机转子的转速为3 000 r/min,压力油孔设置在轴承与轴颈最大间隙处，以减小油孔对油膜稳定性的影响。轴颈半径R=25 mm,宽径比B=0.8,相对顶隙ψ=0.002 4 mm，取不同的椭圆度(ψ/ψ*=1.8,2.4,2.7,3.0,3.5，6.0)建立三维模型，并分别计算不同椭圆度轴承的油膜特性。

图1 椭圆轴承物理模型

计算椭圆轴承油膜特性的关键步骤是画合理的网格，因轴颈与轴承之间的间隙狭小，最大值与最小值之间相差不超过0.2 mm，所以对网格技术提出了很高的要求。因此，采用icem CFD建立网格，运用Delaunay方法生成六面体非结构化网格，它能很好地拟合圆形和椭圆外形，不会忽略边缘细节。网格总数为50～70万个，最小网格长度为5 μm，最大网格长度为10 μm。

2 数值计算数学模型

狭小间隙内的黏性流体系处于高速旋转状态，由于偏心和压力油口的存在，必定存在湍流现象。随着润滑油的流动，黏性流体又趋于缓和，所以采用SST模型进行计算。其中黏性流体的连续性方程为

式中：ρ为流体密度；t为时间；u,v,w为速度。

假设润滑油在流动过程中黏性力不随温度的变化而变化，即不考虑黏温效应，那么不压缩黏性流体的N-S方程可简化为

k-ε模型是典型的湍流模型，在CFD中是最常见的模型，虽然其具有很好的湍流预测能力和数据稳定性，但不能准确预测湍流的开始，特别是流体在负压梯度、脱离壁面的情况下，无法预测脱离总量。湍流是一个三维、非稳态且具有较大规模的复杂流动过程，对计算过程的影响很大。考虑到湍流的剪切应力不可忽视，运用SST模型可以准确预测流动的开始和负压梯度条件下流动的分离量。SST的优点在于它考虑到湍流的自由剪切流动，而且不会对涡流黏度造成过度预测。其中漩涡的黏度方程为

式中：S为应变率；F2为混合函数；w为应变的一个估算；k为单位体积湍动能。

混合函数对模型非常重要，其算式与流体变量和到壁面的距离有关，它的值表示为

本文对9例左冠状动脉异位起源于肺动脉的患者采取多普勒超声检查,结果与李文秀、耿斌、吴江等人[2]的研究结果相似,李文秀等人的研究结果为8例患者的平均左室舒张末内径为(51.36±2.62)mm,平均左室收缩末内径为(34.06±1.92)mm,平均左室射血分数为(69.61±1.02)%,但是李文秀等人的研究将8例患者的结果全部采取表格的形式表现出来,数据清晰,更具研究性,需要本研究进行学习。

式中：y为到最近壁面的距离；ν为运动黏度系数；k为k方程；w为w方程。

3 油膜压力特性值计算及分析

滑动轴承进口油压设置为0.2 MPa，润滑油的动力黏度为0.02 Pa·s，轴承转速为3 000 r/min。为了便于叙述，把最小油膜处的油楔称为第1油楔，把另一个油楔称为第2油楔。图2为不同椭圆度下油膜压力特性，从模拟中可得到，随着椭圆度的增加，第2油楔负压区油膜压力开始增大，之后又随着椭圆度的增加而减小。油膜从圆柱轴承的单油楔过渡到椭圆轴承的稳定双油楔过程需要一定的椭圆度，椭圆度小时，第2油楔形成的油膜承载能力就很小。椭圆度大时，轴承与轴颈之间的间隙变大，油量损失大，油膜力将减小，就很难维持好油膜的完整性，容易发生油膜失稳现象。

图2 不同椭圆度时的油膜压力特性

第1油楔的油膜力变化比较复杂，它属于主要承载区。从模拟图可看出，椭圆度小时，如椭圆度ψ/ψ*=1.8，油楔的油膜压力表现形式近似于圆柱轴承的压力梯度，几乎呈同心圆形状，负压值小；当椭圆度增加，负压区油膜压力梯度逐渐呈现出椭圆形状，且随着轴承椭圆度增加，负压区油膜压力梯度的椭圆形状更加明显，负压值变大。第1油楔的负压区压力值随着椭圆度的变化而变化，也反映着油膜承载能力的变化。

第1油楔正压区变化与负压值变化类似，椭圆度小时，正压区的压力值随椭圆度增加而增大，当椭圆度增加到一定值时，正压区则开始减小。正压区和负压区压力值的复杂变化形式可以理解为：椭圆度小时，轴颈与轴瓦形成油楔的斜率小，润滑油挤压程度不大，故形成的油膜压力也不大；椭圆度在一定范围内，轴颈与轴瓦形成的油楔斜率增大，随着轴颈转动，油膜挤压加剧，形成的油膜压力较大，此时椭圆轴承形成的油膜力比圆柱轴承的油膜力要大；但椭圆度很大时，轴颈与轴瓦之间的间隙很大，流失的油量增多，油膜受挤压程度不足，油膜压力就逐渐减小，甚至大椭圆度时就很难保证油楔的形成。如椭圆度ψ/ψ*=3.5时，负压区的油膜开始变形，而且从计算过程也可知，迭代的曲线开始震荡；当ψ/ψ*=6.0时，正压区的油楔几乎不稳定而且形成的压力梯度也很小，迭代的曲线同样振荡。

因此，椭圆度对压力油膜特性起着很重要的作用。椭圆度较大(如3.5)时，在楔形间隙起始段很难形成承载油膜，使承载油膜变短，轴承承载能力下降，而摩擦阻力增大。椭圆度较小(如1.8)时，加工工艺难以实现，而第2油楔也只能形成很小的承载油膜，所以存在最佳的椭圆度。模拟所得椭圆度引起油膜的变化规律，符合汽轮机实际运行中椭圆度的变化规律；模拟中最佳的椭圆度为2～3，与汽轮机组实际运行中要求的最佳椭圆度相符合[8]。

4 椭圆度对转子稳定性的影响

椭圆轴承2个油楔负压区压力变化均呈抛物线分布，如图3所示。椭圆度ψ/ψ*增加到2.5左右，2个油楔负压区的负压值均增大，油膜压力大，梯度大，压力油膜能提供汽轮机转子更大的承载能力。椭圆轴承与圆柱轴承相比，圆柱轴承间隙增加时油膜力是逐渐减小的，而椭圆轴承有一段油膜力是随椭圆度的增加而增大；另外，椭圆轴承有2个油楔，当椭圆度增加到一定值时，2个油楔的负压区都随椭圆度增加而增大，而圆柱轴承只有1个油楔，间隙变大，油膜力较小。圆柱轴承单油楔对转子稳定性是不利的，转子受到扰动时，单油楔的圆柱轴承抗干扰能力弱，容易引起油膜失稳。椭圆轴承的双油楔可以有效克服转子的失稳。

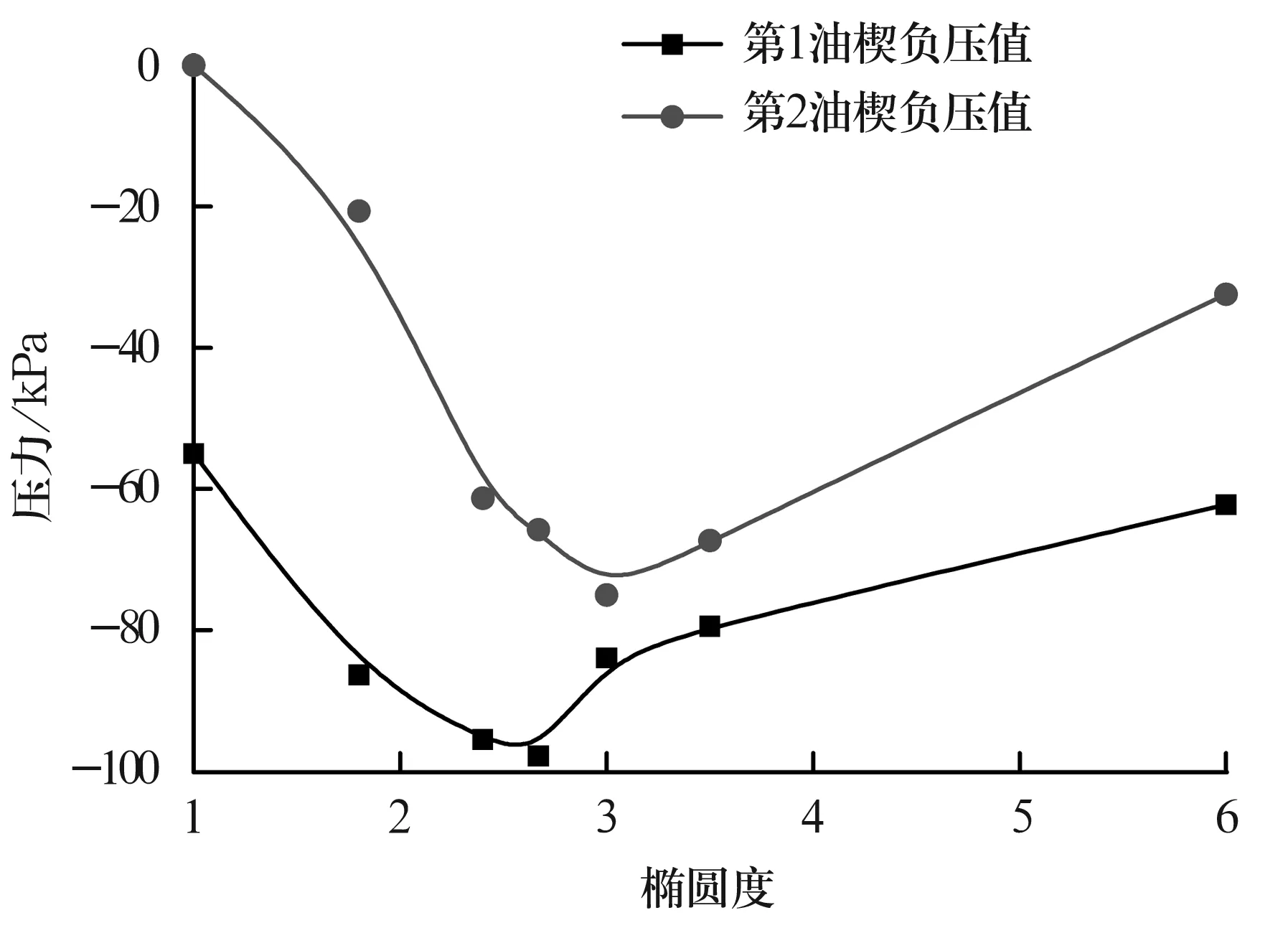
图3 油楔负压值随椭圆度的变化

椭圆度ψ/ψ*>3.0时，第1油楔的压力梯度开始减小，椭圆轴承的承载能力下降，对转子运行不利；第2油楔负压区的负压值也快速下降，油膜承载能力差，转子容易与轴承发生摩擦，也容易发生油膜失稳现象。椭圆度越大，油膜的承载能力越小，如椭圆度ψ/ψ*=3.5和6.0时，承载油膜狭小，出现变形，油膜失稳。

综上所述，椭圆度小时，椭圆轴承第1油楔可承受稳定的载荷，但第2油楔形成的油膜承载能力差；椭圆度大时，不能保持油膜的稳定性。从图2可以看出，椭圆度为2～3时油膜最稳定，正、负压区的油膜完整且不变形，油膜压力梯度比例合理，综合了大和小椭圆度轴承的优点，此时转子的抗干扰能力最强，稳定性最好。

取椭圆度ψ/ψ*=2.7的椭圆轴承与圆柱轴承进行比较，它们的圆周压力分布如图4所示，圆柱轴承和椭圆轴承最小油膜厚度都为0.03 mm。

图4 圆柱轴承和椭圆轴承油膜力沿周向分布

从图中可以看出：椭圆轴承的负压值大于圆柱轴承的负压区负压值，椭圆轴承的油膜压力梯度比圆柱轴承大，分布更加紧凑，而且具有双油楔，也有利于转子在受扰动下保持油膜的完整性，确保转子安全可靠运行。

5 结论

(1) 在轴承与轴颈相同最小间隙下，当椭圆度一定时，椭圆轴承比圆柱轴承具有更大的油膜力，能承受转子更大的载荷。

(2) 椭圆轴承比圆柱轴承油膜压力梯度大，压力油膜更加稳定，使转子运行的稳定性提高。

(3) 椭圆轴承具有双油楔，转子运行过程中不容易发生油膜振荡和失稳现象。