圆柱滚子轴承外圈轴向温度分布研究
2012-07-20李凌鑫李济顺李伦胡伟奇
李凌鑫,李济顺,,李伦,胡伟奇
(河南科技大学 a.机电工程学院;b.河南省机械设计及传动系统重点实验室,河南 洛阳 471003)
大多数轴承工作在远低于额定转速和额定载荷的情况下,不必特别考虑过热的问题,但在转速接近额定转速、载荷接近额定载荷的工况下长时间工作,发热量会很大。如果热量不能及时散发,轴承温度将异常升高,引起润滑剂黏度下降,滚子与滚道磨损加速,甚至接触面材料回火软化,导致轴承过早疲劳失效,更严重的将导致轴承胶合咬死,后果十分严重。因此,需要考虑外部冷却系统来降低轴承系统的温度,保证轴承在合理的温度范围内正常运转。
在轴承外圈表面与轴承座之间开槽通入冷却液是一种有效的冷却方法,但是槽的数量、尺寸、位置以及槽的分布取决于轴承外圈表面的温度分布。本例以圆柱滚子轴承为研究对象,分析其在不同工况下外圈表面的温度分布情况,为轴承外部冷却系统的设计提供理论依据。
1 轴承发热量的计算
轴承在运转过程中,会因各运动部件之间的摩擦而引起能量损失,在轴承系统中表现为温度的上升。因此,对轴承发热量的计算首先是对摩擦力矩的计算。
轴承摩擦力矩是个十分复杂的问题, 涉及到接触力学、摩擦学等多个学科,各种因素相互作用,又相互干扰,对轴承发热量的计算造成了一定困难。文献[1]提出要准确地计算轴承的摩擦力矩,需要考虑导致摩擦的4个原因
M=Mrr+Msl+Mseal+Mdrag,
(1)
式中:M为总摩擦力矩;Mrr为滚动摩擦力矩;Msl为滑动摩擦力矩;Mseal为密封件的摩擦力矩;Mdrag为由于拖曳损失、涡流和飞溅等导致的摩擦力矩。
该方法根据导致摩擦的根本原因进行分析,并把各种因素结合起来计算总的摩擦力矩。
对于圆柱滚子轴承
(2)
(3)
(4)
(5)
式中:Dpw为滚子组节圆直径,mm;Fr为径向载荷,N;ν为润滑剂的运动黏度,mm2/s;n为转速,r/min;R1,S1和S2为摩擦力矩的几何常数;Fa为轴向载荷,N;μsl为滑动摩擦因数;Ks1,β和Ks2分别为根据轴承类型和密封件类型而定的常数;ds为轴承肩部的直径;VM为拖曳损失变量;Kroll为用于滚子轴承的常数;B为轴承内圈宽度,mm。
为了更准确地进行计算,SKF新模型考虑了切入发热和贫油回填效应等因素的影响,并加入到总摩擦力矩M的计算公式中
M=φishφrsMrr+Msl+Mseal+Mdrag,
(6)
φish=[1+1.84×10-9(nDpw)1.28ν0.64]-1,
(7)
(8)
式中:φish为切入发热减少系数;φrs为贫油回填减少系数;Krs为贫油回填常数;Kz为轴承类型相对应的几何常数;d和D分别为轴承内径和外径,mm。
计算出摩擦力矩后,便可用下式算出摩擦功耗
Hf=1.047×10-4nM。
(9)
2 传热模型的建立
对一个给定转速和载荷的轴承工作状态,其最终的稳态温度分布会受到各种复杂传热过程的影响,其中涉及传热学、流体力学等多种学科,而传热过程中的对流换热问题更是难以确定。因此轴承最终的温度分布结果是很难精确计算的,要模拟轴承的发热及传热过程并求出局部温度分布,需要做出适当假设来简化模型。
图1为圆柱滚子与外圈滚道的接触区域示意图。轴承在工作时圆柱滚子与套圈滚道的接触位置不断发生变化。滚子与接触区域的接触和分离是间断出现的。当滚子在滚道中滚动时经过接触区域,由于摩擦发热,接触区域实际上就成为热源。接触区域及周围材料温度升高,而滚子与接触区域在下一时刻分离后,又被周围介质冷却,接触区域及周围材料温度降低。因此滚道中滚子经过接触带面上的每一个表面都在经历不断的加热和冷却的循环,最终达到稳态的温度场[2]。

图1 滚子与外滚道接触区域示意图
对于高速圆柱滚子轴承,接触区域冷却的时间间隔极短,每次产生的热量要通过接触区域向滚子和滚道的表面和内部传递,然后达到稳定状态,所以接触区域可视为一个热源。但对于高速运转的轴承来说,每个接触区域一秒钟可被加热几百次,为了简化计算,对高速轴承可以视接触区域为恒定热源,取滚道中任一套圈横截面为研究对象,分析其传热及截面稳态温度分布情况,这样可大大减少计算量。图2以内圈引导圆柱滚子轴承为例给出了内、外圈和滚子截面示意图。
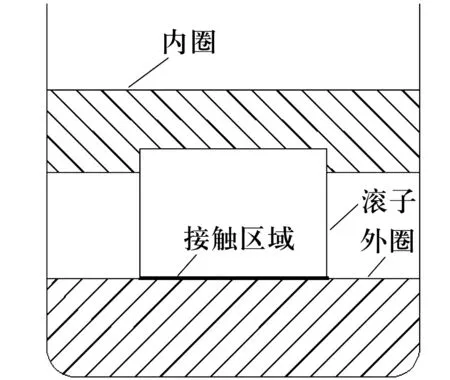
图2 圆柱滚子轴承截面示意图
由于轴承零件材料的物理性质(热传导系数、比热容、密度)相同或相似,因此摩擦产生的热量在参与接触的滚子与滚道接触表面按1∶1分配[3]。假设轴承在运转过程中,外圈固定,内圈转动。由于滚子与内、外圈滚道同时发生摩擦,内、外圈相对角速度相同,内圈相对滚子线速度大于外圈,因此在轴承内圈转动一周的过程中,滚子与内圈摩擦次数要大于与外圈的摩擦次数。此外滚子与内滚道之间的接触应力要高于与外滚道之间的接触应力,因此,内滚道发热量要高于外滚道。轴承外圈不仅要吸收与滚子摩擦产生的热量,而且还要吸收通过滚子传导的内滚道摩擦热。
本例旨在研究轴承运转达到稳态传热的情况下,外圈外表面的温度分布,故在此对轴承内圈、保持架等的发热及传导不再详述。只考虑稳态传热的情况下,轴承摩擦产生的热量通过图3所示接触区域向外圈传导。

图3 外圈滚道截面示意图
图3中滚子与滚道接触面为热传导,滚道表面承受润滑剂的对流换热。由于热量向摩擦机体内的传播不取决于辐射,因此在计算中忽略辐射散热对外圈表面温度分布的影响,只考虑滚道表面热传导和通过外圈的导热,以及最终在AB面上的温度分布。
热流网络法在分析系统中选择一些温度节点,不同的温度节点之间用不同的热阻相互联系形成热网络,利用稳态传热中每个节点上流入和导出的热流量相等的原理建立热流方程组[4],以此来求解轴承温度分布。图3所示截面左右对称,传热及换热表面也左右对称,因此取左边一半为研究对象建立传热模型如图4所示,通过热流网络法求解其温度分布。

图4 传热计算模型
图4在稳态传热的情况下在轴承外圈滚道不同的位置建立了5个温度节点:其中,①为滚子与滚道接触区域中心温度T1;②为外表面轴向中心位置温度T2;③为外表面边缘温度T3;④为滚道与滚子未接触区域温度T4;⑤为油温T5;A为环境温度。其中①有热量传入;①,④和⑤之间有对流换热;②,③和⑤与环境温度之间有对流换热。
5个节点之间的热量传递关系见表1。

表1 传热系统
其中摩擦生热用(9)式计算,摩擦力矩用(6)式求出。热传导计算式为
(10)
式中:S为垂直两点间热流方向的面积;d为这两点间的距离;k为材料导热率。
固体表面的热对流通常描述为
Hv=hvS(T1-T2),
(11)
式中:hv为对流换热系数,它是固体表面及流体的温度、流体的导热率、靠近固体表面的流体速度、表面尺寸、流体黏度及密度的函数。其可以用Harris给出的近似计算式计算[4]
(12)
Pr=Cpρν/λ,
(13)
Re=ul/ν,
(14)
式中:λ为润滑油导热系数;Pr为润滑油的Prandtl数;Re为润滑油的Reynolds数;Dpw为滚子组节圆直径;Cp,ρ分别为润滑油的比热容和密度;u和l分别为流体的特征速度和特征长度。
在稳态传热中,每个节点上流入的热流量应等于流出的热流量。因而,流经每个温度节点的热流量之和等于零。以节点1为例,流入、流出的热流量之和为零,即
H1-1+H2-1+H3-1+H4-1+H5-1=0。
(15)
根据表1列出的关系,把相应的(9)~(11)式代入(15)式,可列出图4所示模型的热流方程组
(16)
(17)
(18)
(T3-T4)+hvS4(T5-T4)=0,
(19)
hv1S5(TA-T5)+hvS1(T1-T5)+
hvS2(T4-T5)=0 。
(20)
3 算例与结果分析
选用NU313单列圆柱滚子轴承作为算例进行传热计算,轴承内、外圈及滚子材料为8Cr4Mo4V。表2为NU313轴承的基本结构尺寸。
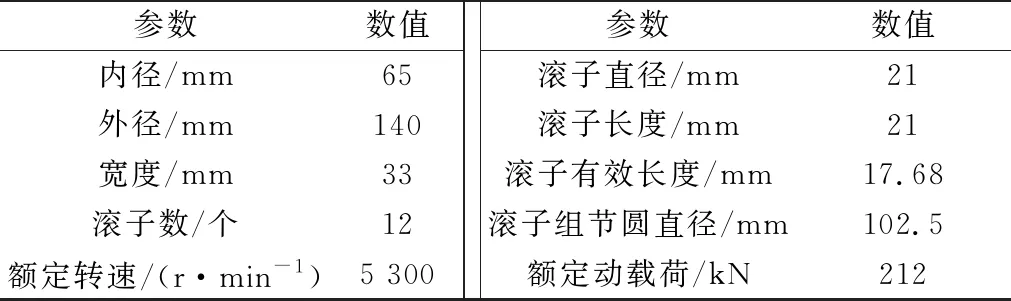
表2 NU313轴承基本参数
把相应数据代入该传热系统的热流方程组,在这里,取环境温度为30 ℃,润滑油运动黏度为20 mm2/s,轴承材料导热率为42 W/(m·k),可计算出不同工况下各节点的温度分布情况,如图5~图8所示。
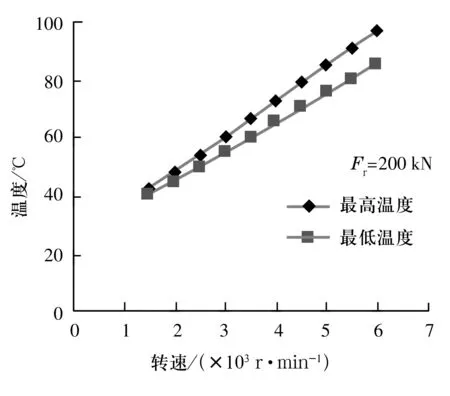
图5 载荷一定时模型中极值温度与转速关系

图6 不同转速时各节点的温度分布
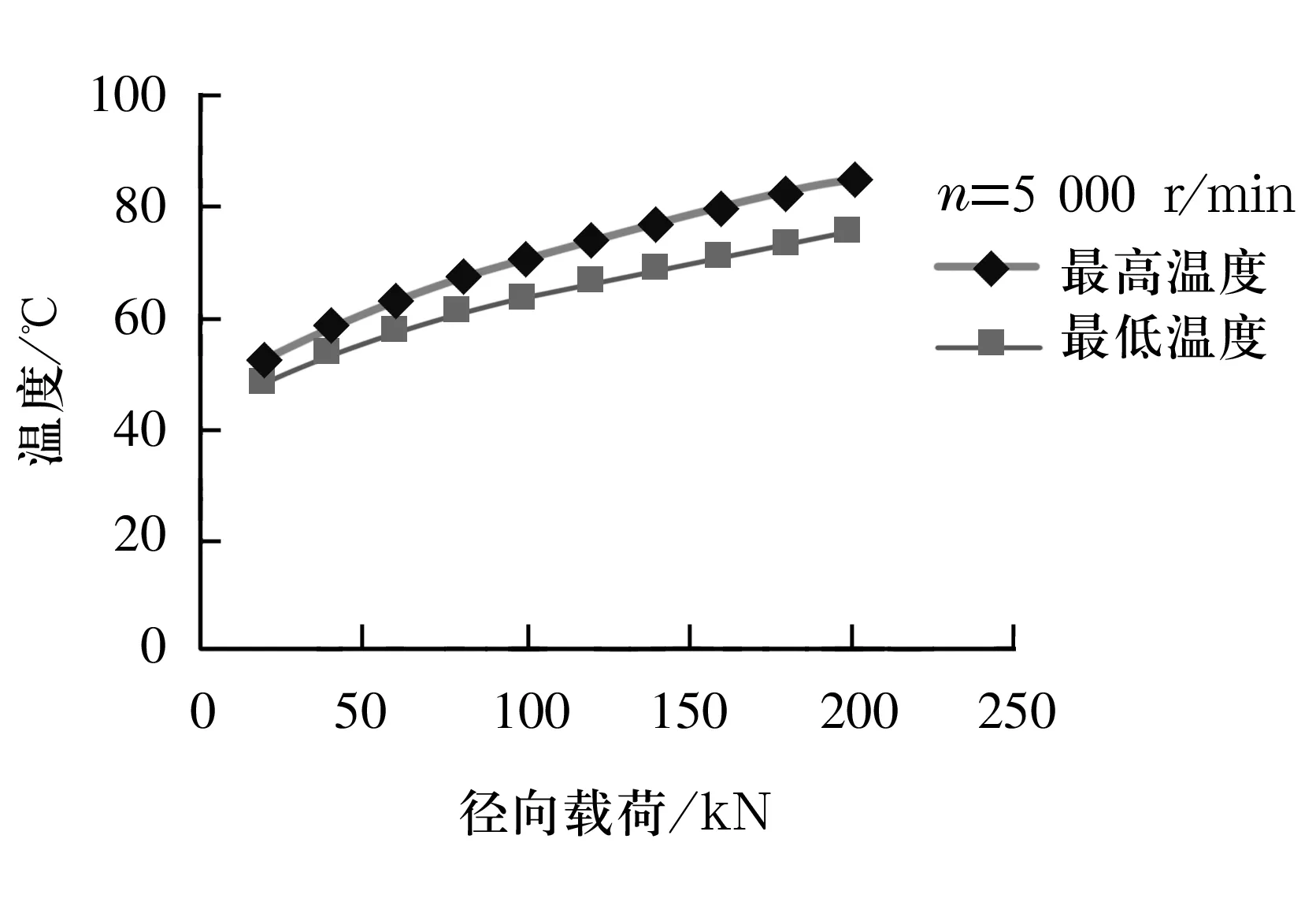
图7 转速一定时模型中极值温度与载荷关系
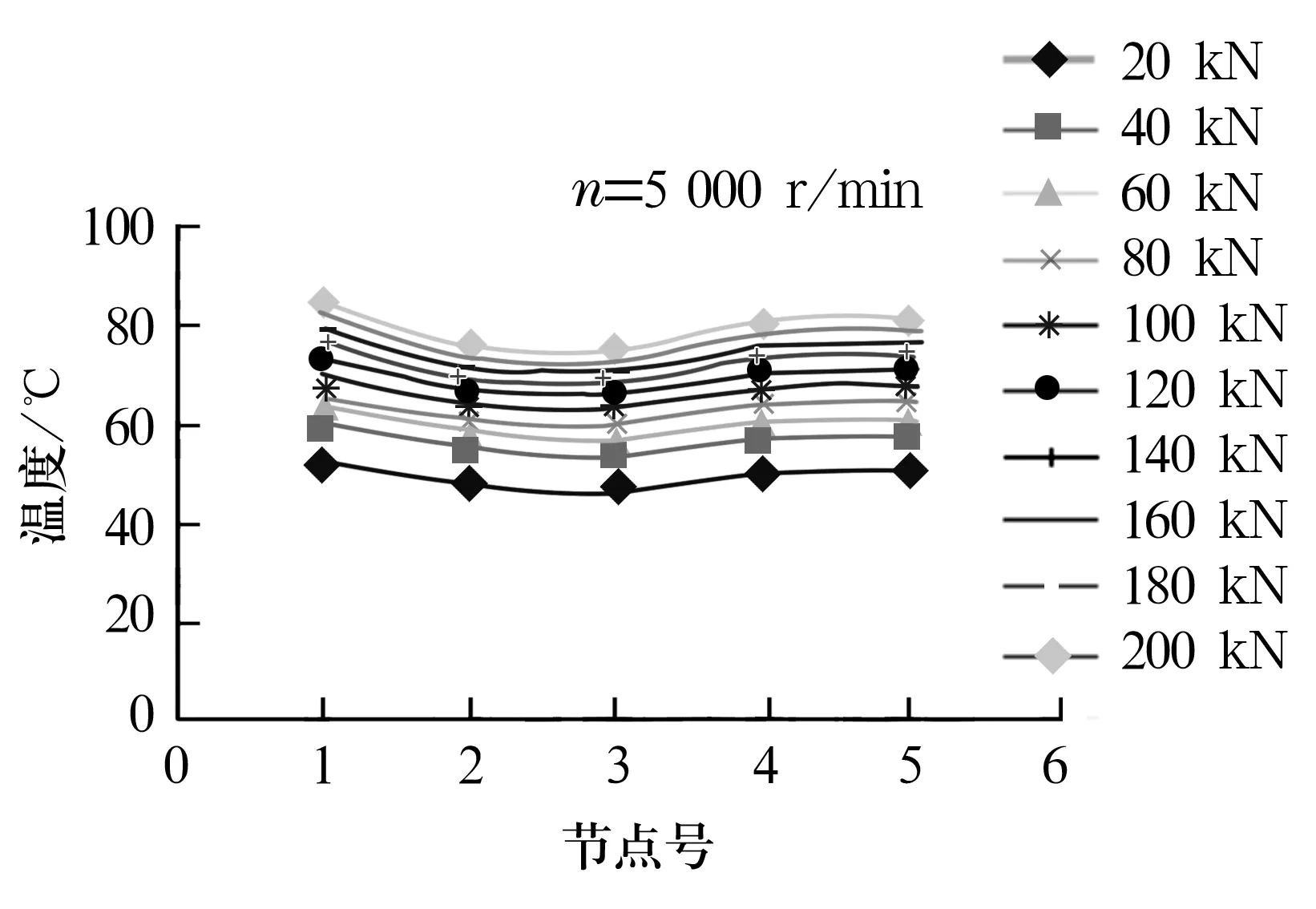
图8 不同载荷时各节点的温度分布
如图所示,温度最高点出现在节点1处,最低点出现在节点3处。节点2和节点3分别为外表面的温度最高点和最低点。
4 结束语
通过对轴承外圈截面的传热分析可知:(1)轴承外圈外表面温度随轴承所受载荷的增大而升高,随转速提高而升高;(2)轴承外圈外表面温度相差最多不超过1%,可以按照沿轴向温度均匀分布来处理。
基于此,如果要在轴承外圈和轴承座之间开槽来给轴承降温,可以选择开几条尺寸相等的槽,并使其均匀分布。至于槽的开口位置和几何参数,需要另外考虑轴承外圈外表面的周向温度分布。
