采用霍尔传感器的PMSM低成本控制系统

黄腾云，姜淑忠，李小海

(上海交通大学，上海200030)

0 引 言

永磁同步电动机(以下简称PMSM)由于其具有功率密度大、效率高、转子损耗小、噪声低等优点，广泛应用家电设备、机器人、电动车、电动医疗器械等领域。

PMSM为了产生平滑的转矩以及减小电磁噪声和转矩脉动，因此需要高分辨率的转子位置传感器，例如:光电编码器、旋转变压器等［1－2］。但是这类传感器的使用不仅使得系统成本变高，并且易受高温、高湿等恶劣环境的影响。为了使PMSM不用这类高分辨率的位置传感器，目前产生了很多无传感器的转子位置观测算法，但这些算法在起动和低速时容易出问题。霍尔传感器具有价格便宜、运行可靠的优点，近年来被广泛应用于正弦波驱动［3－4］。

针对系统对转子位置分辨率要求不高但对成本有苛刻要求的场合，如家用洗衣机应用场合，本文设计了一种采用霍尔传感器作为转子位置反馈的PMSM控制系统。该系统采用三个霍尔元件提供转子位置信号，控制器利用转子信号算出转子位置和转速计算输出正弦波的位置角和幅值，进而计算出PWM波形的输出脉宽，形成全数字的PMSM控制系统。

1 PMSM数学模型

图1给出了一台两极PMSM的结构示意图。对于这种电机，可得出在静止坐标系下的电压方程和磁链方程［5］:

图1 两极PMSM结构示意图

式中:u、i、ψ分别为A、B、C三相绕组的相电压、相电流和磁链;R为每相绕组的电阻。

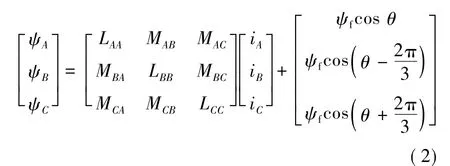
式中:Lii为每相绕组的自感;Mij为两相绕组的互感;ψf为转子永磁体的磁链;θ为转子位置。PMSM的自感和互感可用下式表示:

式中:Lσ、Lav、Ls分别为绕组自身的漏电感，主电感平均值和转子相关电感量。

由以上各式可知，转子位置θ与电机本身的参数(绕组电阻、电感和转子永磁体的磁链)共同决定着电机的相电压、相电流和磁链。PMSM的电磁转矩可表示［6］:

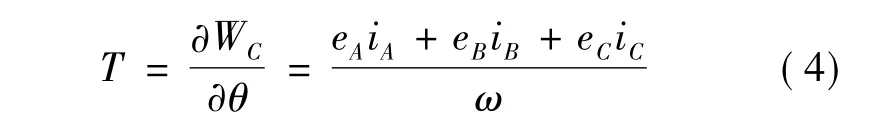
其中:伴随能WC= ∫ψAdiA+ ∫ψBdiB+ ∫ψCdiC，ω 为转子电角速度，ei为各相的反电动势:

由式(4)和式(5)可知，如果反电动势波形与相对应的相电流波形不一致将会产生转矩脉动以及电磁噪声。因此，要将反电动势为正弦波的PMSM的转矩脉动降到最低，必须使PMSM的相电流为正弦波，即iA=Imsin θ，其中Im为电流幅值，则可得电磁转矩表达式:

2 控制策略

相电流为正弦波时，由式(6)可知，PMSM的电磁转矩为恒定值并且与转子位置无关。定子绕组端电压为反电势、电枢绕组电阻压降和电枢绕组电抗压降矢量和，在家用洗衣机等对动态响应要求不高的场合，可认为加在定子端的相电压近似等于反电动势。因此可通过在PMSM输入如式(7)的相电压来产生与反电动势相对应的正弦波相电流:

式中:V*为相电压幅值。

图2为PMSM的控制框图。当电机运行时，操作面板给定的转速ω*减去通过霍尔传感器估算得来的转速ω，转速误差Δω通过转速PI调节器得出正弦波的幅值V*。由式(7)可知，只要算出转子位置θ就可以得到三相互差120°的正弦波相电压，而转子位置信息可通过对霍尔元件的输出信号进行估算来得到。在完成上述任务后，通过规则采样法或等面积法可算出6路PWM所输出的脉冲宽度。

图2 PMSM控制框图

3 转子位置与转速的估算

由图1所示，A、B和C三相对称绕组互差120°电角度，三个霍尔元件也互差120°电角度，安装在PMSM的定子上。当霍尔元件在S极上时，它的输出为高电平，否则，输出为低电平。PMSM连续旋转时，三个霍尔元件的输出信号如表1所示。由表1可知，霍尔信号为三相相隔120°电角度的方波，且各有180°的有效角度，这些信号把360°电角度分为6个60°电角度的霍尔扇区。也就是说每一个电周期，三个霍尔元件的分辨率为6个脉冲，显然直接用这6个状态来产生正弦波是不够的，因此需要来估算转子的位置和转速。

表1 霍尔元件输出信号

假设两个相连的霍尔状态所间隔的时间为t，微处理器可通过定时器捕捉功能来记录下这个值，在这个区间内，电机的平均角速度:

Capponi从泰勒展开式的角度阐述转子位置和速度观测算法，提出了零阶算法和一阶算法［7］，即:

式中:θn为当前计算得到的转子位置角度;Ts为采样时间即一个载波周期;α为平均加速度，即:

在通过以上算法得到PMSM的转子位置信息后，微处理器还需要检查估算得到的转子位置是否在所期望的期间内。例如，估算出来的转子角度应满足30°≤θn+1≤90°，如果得到 θn+1＜30°或 θn+1＞90°，则将修正为 θn+1=30°或 θn+1=90°。并且微处理器在每进入一个新的霍尔扇区时进行一次转子位置校正，以消除误差的累积。

上述算法随着阶数的增加，转子位置的误差必然会降低，但是会给微处理器增加负担。在家用洗衣机应用场合，使用零阶算法就可以满足要求。因而可以采用8位单片机来完成对转子位置的估算，以达到节省成本的目的。

4 实验结果及结论

控制系统由整流电路、驱动电路、三相逆变电路、逻辑控制电路和PMSM构成，如图3所示。

图3 系统构成框图

所用的电机为一台12极、功率为200 W的PMSM。本文根据上述的控制思路进行了大量的实验，实验证明系统可靠、有效。图4为转速为500 r/min时的两相电流波形。图5为运转1.5 s后停止的一相电流波形，从波形可以看出，PMSM的起停是快速、安全和有效的。

本文采用三个霍尔传感器作为反馈信号，通过8位单片机对霍尔信号进行转子位置和转速估算，与给定转速进行比较，进而对PWM输出脉宽进行调节实现电流的正弦换流。实验结果表明，本文所构建的控制系统不仅有很好的控制效果，而且又达到了节约成本的要求，具有广阔的应用前景。

图4 转速为500 r/min的电流波形

图5 运转1.5 s后停止的电流波形

［1］ Pillay P，Krishnan R.Application characteristics of permanent magnet synchronous and brushless DC motors for servo drives［J］.IEEE Transactions on Industry Applications，1991，27(5):986 －996.

［2］ Bu J，Xu L，Sebastizn T，et al.Near－ Zero Speed Performance Enhancement of PM Synchronous Machines Assisted by Low Cost Hall Effect Sensors［C］//Proc of IEEE APEC＆ 98.1998:68 －74.

［3］ Batzel T D，Lee K Y.Slotless permanent magnet synchronous motor operation without a high resolution rotor angle sensor［J］.IEEE Trans.on Energy Conversion，2000，15(4):366 －371.

［4］ Mori Moto S，Sanada M，Takeda Y.Sinusoidal current drive system of permanent synchronous motor with low resolution position sensor［C］//Proc.1996 IEEE IAS Annual Meeting.San Diego，CA，USA:［s.n.］，1996:9 －14.

［5］ 谢宝昌，任永德.电机的DSP控制技术［M］.北京:北京航空航天大学出版社，2005.

［6］ Todd D Batzel，Kwang Y Lee.Commutation torque ripple minimization for permanent magnet synchronous machines with Hall effect position feedback［J］.IEEE Transactions on Energy Conversion，1998，13(3):257 －262.

［7］ Capponi F G，De Donato G，Del Ferraro L.Brushless AC Drive Using An Axial Flux SynchronousMotor With Low Resolution Position Sensors［C］//Proc.of IEEE 35th Annual Power Electronics Specialists Conference.2004:2287 －2292.