基于改进UKF滤波的永磁同步电动机矢量控制

许 波，朱熀秋，姬 伟

(江苏大学，江苏镇江212013)

0 引 言

永磁同步电动机具有结构简单、体积小、重量轻、转矩惯性比高、能量密度高、动态响应快、过载能力强等优点，近年来在航空航天、电动汽车、工业控制领域获得了越来越广泛的应用。永磁同步电动机矢量控制是通过控制定子电流矢量来间接控制电磁转矩，这种方法实现的关键在于能否获得精确的转子位置，故对位置传感器的要求较高。传统的转子空间位置和速度都是采用机械式传感器(光电编码器、旋转变压器等)来检测，存在安装、连接、可靠性等问题，因此，无传感器矢量控制技术成为研究热点。

目前，按照电机运行的适用范围，无传感控制主要分为两种:(1)信号注入法［1－2］，通过施加高频、低频激励，追踪电机转子的空间凸极效应，该方法具有对电机参数变化不敏感、鲁棒性好等优点，更适合实现零速及低速范围内转子位置的有效检测。但该方法存在高频信号处理问题，高频电流信号提取的好坏直接影响到转子位置和速度的估计。2)状态观测法［3－9］，直接或间接地从电机反电动势中提取位置信息。如直接计算法［3］，扩展反电动势法［4］;基于模型参考自适应的估计器［5］、滑模预测估计器［6］、基于扩展卡尔曼滤波器［7－8］的估计器及基于人工神经网络估计法［9］等。这类方法具有良好的动态性能，更适合于中高速场合。这类方法中，由于EKF对非线性系统优异的状态估算能力及其本身的抗干扰能力，因而在感应电机转速估计中引起了广泛的关注。文献［7］提出了一种变参数EKF估算方法，即在动态和稳态过程中，分别给出一组固定的噪声协方差矩阵参数，保证了EKF良好的估算性能，能够同时满足系统动态过程和稳态运行时的应用要求。文献［8］从电机数学模型和电机本体设计方面出发，提出协方差矩阵的设定方法，有效地解决了EKF方程中各协方差的初始设定，使EKF更易于工业化应用。UKF(Unscented Kalman Filtering)是近年来在EKF基础上发展起来的新算法，UKF避免了EKF线性化所带来的误差，估计的均值和协方差达到Taylor级数的四阶精度［12］，且不需要计算非线性方程的Jacobi矩阵。基于UKF的感应电机的无传感器估计研究取得了一定的效果［10－11］。但UKF与EKF一样，仍存在模型不确定性的鲁棒性差、对突变状态的跟踪能力降低和收敛速度较慢问题。而强跟踪滤器(Strong Tracking Filter－STF)作为一种自适应滤波器，具有独特的强跟踪能力［13］，可以有效地改善系统对模型不确定性及突变状态的跟踪性能。基于上述分析，本文结合强跟踪滤波器对UKF进行改进，引入时变渐消因子在线自适应调整增益矩阵状态预测误差协方差矩阵，以实现残差序列正交或近似正交，强迫UKF保持对实际状态的快速跟踪。构建永磁同步电动机无速度传感器控制系统，采用改进UKF进行永磁同步电动机转子位置及速度估计，并通过数字仿真，验证算法的有效性。

1 改进UKF滤波

1.1 UKF 算法

考虑一大类非线性系统:

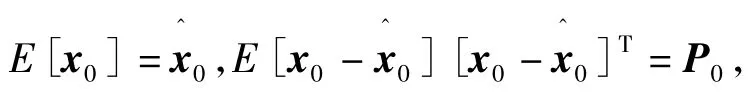
基于UKF滤波的状态估计实现步骤:

(1)初始化状态x和状态误差协方差阵P0。

(2)每个采样周期内(k=1，2，…，∞)计算Sigma点:

(3)状态更新。对每个Sigma点进行非线性变换并取均值:

(4)测量更新

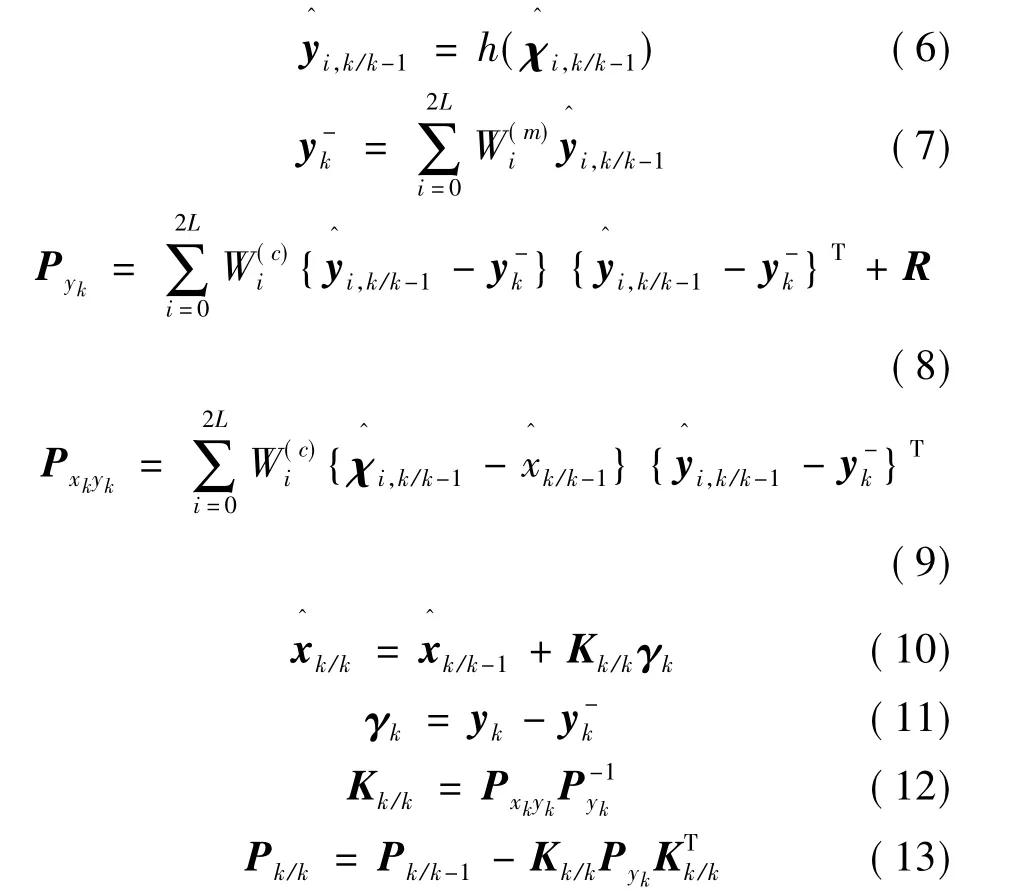
1.2 改进UKF算法

强跟踪滤波［12］是在EKF基础上发展起来的滤波算法，具有较强的对模型不确定性的鲁棒性，极强的对突变状态的跟踪能力。它满足以下正交条件:

式中:γk为残差序列，且γk=yk－。

本文结合强跟踪滤波器，通过对UKF引入时变渐消因子来在线自适应调整增益矩阵和状态预测误差协方差矩阵，实现残差序列正交或近似正交，强迫UKF算法保持对实际状态的快速跟踪，达到强跟踪效果。文献［12］给出EKF满足强跟踪滤波时增益阵Kk/k的选取原则。同理可证，下式

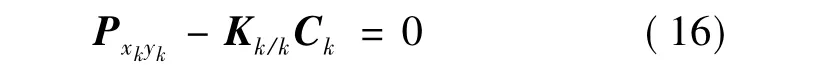
成立，则UKF满足式(15)。此时，UKF成为强跟踪滤波器。

引入时变渐消因子λk，则Kk/k可以表示:

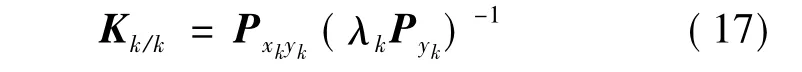
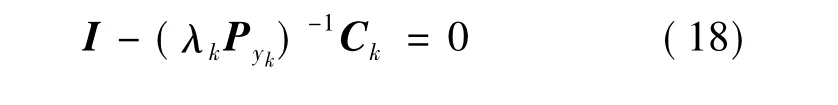
对上式求迹，得:

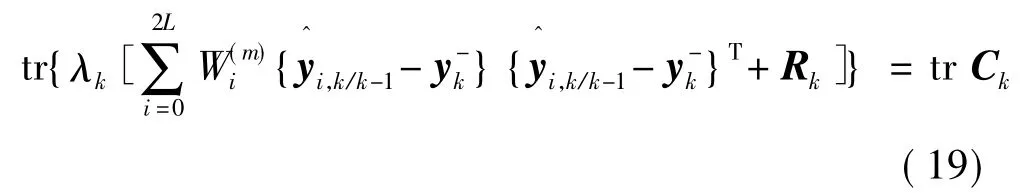
式(19)可转化:

2 永磁同步电动机数学模型

永磁同步电动机采用矢量控制，在α－β坐标系下，选取状态变量:x=［iαiβω θ］T，控制变量为:u=［uαuβ］T，输出变量 y=［iαiβ］T，因此永磁同步电动机的状态方程:

式中:uα、uβ为 α － β 坐标系下定子电压;Ld、Lq为等效两相定子绕组的dq轴自感;F为转子与负载的摩擦系数;Ψ为永磁磁极与定子绕组交链的磁链;Te、Tm分别为电磁转矩和机械转矩;P1为转矩绕组极对数;J为转子的转动惯量;θ为转子位置角;ω为转子角速度。

测量方程:

将式(21)和式(22)离散化，设采样周期为T，且控制信号在采样周期内基本不变。设在时刻k状态变量 xk= ［iα，kiβ，kωkθk］T，控制变量 uk=［uα，kuβ，k］T，输出变量 yk=［iα，kiβ，k］T，考虑系统噪声影响，则永磁同步电动机离散化后的状态方程与输出方程可用式(1)描述。

3 基于改进UKF滤波的永磁同步电动机无速度传感器运行仿真试验

3.1 无速度传感器矢量控制系统构成及仿真

图1给出了包括转速控制和转子位置及速度自检测在内的基于改进UKF滤波的永磁同步电动机无传感器矢量控制系统框图，采用id=0控制策略，θ1为负载角。

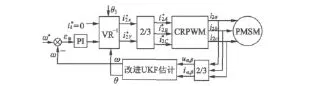
图1 基于改进UKF的永磁同步电动机无速度传感器矢量控制原理框图

电机选用MATLAB自带模型，转动惯量J=5.6×10－4kg·m2，极对数 p1=4，定子电阻2.875 Ω，定子直轴与交轴电感为8.5 mH，永磁磁极与定子绕组交链的磁链为0.175 Wb。系统仿真中采样选用变步长，仿真模式ode23s，仿真时间为0.1 s，给定速度范围为0～6 000 r/min。速度和位置估计模块采用S函数实现Simulink与M文件接口。

改进UKF采样周期为1×10－5s，初始状态为0，估计误差协方差初始值 P0=diag(0.1，0.1，200，10)，过程噪声协方差阵和测量噪声协方差阵分别为 Qk=diag(10－6，10－6，10－2，10－5)和Rk=diag(0.1，0.1)，θ1=0。

图2(a)、图2(c)和图2(e)分别表示电机转速为6 000r/min、从6 000 r/min突变至1 000 r/min时空载起动转速曲线及0.04 s加10 N·m的负载扰动时转速变化曲线，图2(b)、图2(d)和图2(f)为其对应的转子角度估计误差曲线。从图中可以看出，在高速、转速突变及负载扰动状态下，基于改进UKF滤波的无传感器运行较UKF方法响应更快，跟踪更准，误差更小，鲁棒性更强。

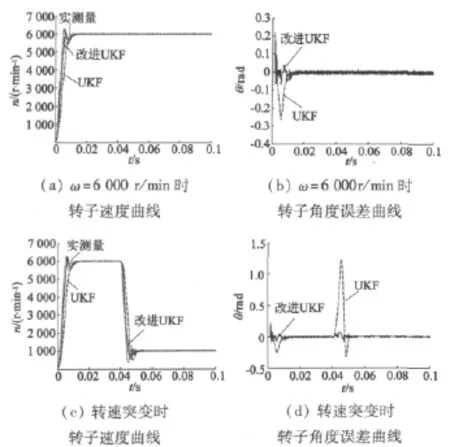
图2 无速度传感器运行下转子速度与转子角度误差曲线

3.2 误差比较与算法复杂度分析

定义均方误差MSE为系统估计质量评价标准，则:

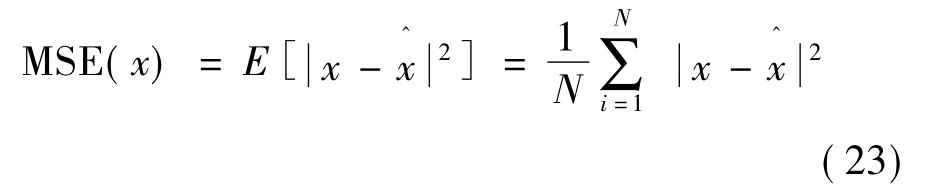
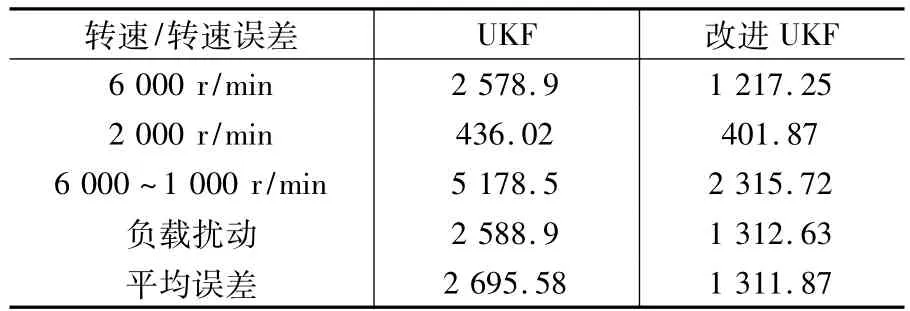
表1 转速估计均方误差表

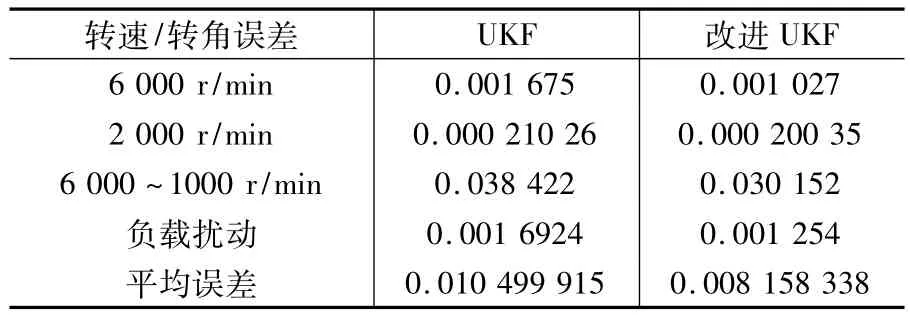
表2 转子角度估计均方误差表

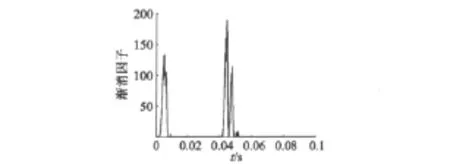
图3 转速突变时渐消因子取值曲线

与UKF相比，改进UKF算法复杂度主要增加在系统残差计算及渐消因子的选取上。图3是系统转速从6 000 r/min突变到1 000 r/min时的系统渐消因子选取曲线，从图中可以看出，在转速变化时，通过渐消因子的选取使转速更逼近实际转速，而在稳态时，渐消阵取值为1，系统退化为普通UKF。

4 结 语

本文对基于改进UKF滤波的永磁同步电动机无速度传感器运行进行了仿真实验研究。通过比较低速、高速、转速突变、负载扰动等情况下转速估计及转子角度估计效果及误差分析，可以看出改进UKF算法较普通UKF算法性能优越，其稳态时保持了UKF的优良性能，与UKF估计精度相同，在转速突变及负载扰动时，能够准确估计电机实际状态，响应速度更快，精度更高，显示出良好的有效性和鲁棒性。

［1］ Piipo A，SalomJ，Luomi J.Signal injection in sensorless PMSM drives fquipped with Inverter output filter［J］.IEEE Transactions on Industry Applications(S0093 － 9994)，2008，44(5):1614 －1620.

［2］ Eskola M，Tuusa H.Sensorless Control of Salient Pole PMSM Using a Low －frequency Signal Injection［C］//European Conference on Power Electronics and Applications.2005:10 －14.

［3］ Kulkarni A B，Ehsani M.A Novel Position Sensor Elimination Technique for the Interior magnet Synchronous Motor Drive［J］.IEEE Transactions on Industry Applications(S0093 － 9994)，1992，28(1):144－150.

［4］ Hasegawa M，Hatta H，Matsui K.Adaptive Flux Observer on Stator Frame and Its Design Based on Positive Real Problem for Sensorless IPM Drives［C］∥32nd Annual Conference of IEEE Industrial Electronics Society，IECON，2005:6 －10.

［5］ 齐放，邓智泉，仇志坚，等 基于MRAS的永磁同步电机无速度传感器［J］.电工技术学报，2007，22(4):53 －58.

［6］ Han Yoon － Seok，Choi Jung－ Soo，Kim Young － Seok.Sensorless PMSM Drive with a Sliding Mode Control Based Adaptive Speed and Stator Resistance Estimator［J］.IEEE Transactions on Magnetics(S0018 －9464)，2000，36:3588 －3591.

［7］ 安群涛，孙力，李波.永磁同步电机转速的变参数EKF估算方法［J］.电机与控制学报，2007，11(6):559 －563.

［8］ Bolognani S，Tubiana L，Zigliotto M.Extended kalman filter tuning in sensorless PMSM drives［J］.IEEE Transactions on Industry Applications，2003，39(6):1741 －1747.

［9］ Ben Brahim L，Kurosawa R.Identification of induction motor speed using neural networks［C］∥ IEEE Power Conversion Conference.Yokohama，1993，689 －694.

［10］ 余佩琼，陆亿红，王涌，等.永磁直线同步电动机无位置传感器控制系统的研究［J］.中国电机工程学报，2007，24(27):53－57.

［11］ 曲智勇，姚郁，韩俊伟.基于改进型平方根UKF算法的永磁同步电机状态估计［J］，电机与控制学报，2009，3(13):452－457.

［12］ Julier S，Uhlmann J，Hugh F，et al.A new method for the nonlinear transformation of means and covariances in filters and estimators［J］.IEEE Transactions on Automatic Control，2000，45(3):477－482.

［13］ 周东华，叶银忠.现代故障诊断与容错控制［M］.北京:清华人学出版社，2000，60－76.