基于不对称振动模态的毫米级直线超声波电动机的研制

张健滔，朱 华，赵淳生

(1.上海大学，上海200072;2.南京航空航天大学，江苏南京210016)

0 引 言

随着微机械、微电子技术的快速发展，对微型作动器的需求越来越多。在微型机器人、微型飞行器、微型医疗设备、微型照相聚焦镜头等微机电系统中，往往需要毫米级的微型作动器。微型超声波电动机由于具有结构简单、易于微型化、功率密度大、无需减速机构、定位精度高等特点，在微机电系统驱动领域有着广阔的发展前景，有着其他类型作动器难以替代的作用［1－6］。

正因如此，毫米级微型超声波电动机的研究备受众多国内外学者的关注。Takeshi Morita等人利用在金属体表面沉积压电薄膜的方法研制了外径1.4 mm、内径1.2 mm、长 5 mm 的微型旋转超声波电动机［7］。Serra Cagatay等人研制了外径1.6 mm、内径0.8 mm、长6 mm的旋转超声波电动机［8］。董蜀湘等人利用四分区极化的PZT管作为定子，研制出直径1.5 mm、长7 mm的微型旋转超声波电动机［9］。周铁英等人利用压电柱作为定子，研制出直径1 mm、长5 mm的旋转超声波电动机［10］。New Scale Technology公司研制了一款定子尺寸为1.55 mm×1.55 mm×6 mm的微型直线超声波电动机［11］。以上文献中，除了文献［8］，所报道的电机都是利用两个频率相同、空间正交的的对称振动模态工作。文献［8］报道的是一款旋转微型超声波电动机，其利用两个空间正交但频率不相等的不对称振动模态工作，文献仅对该电机的运动机理进行了简要的分析。本文将介绍一款基于不对称振动模态的直线超声波电动机的研制，详细分析其运动机理，推导电机单相和两相驱动时驱动质点的运动轨迹方程，进行有限元建模和仿真分析，以及制作原理样机，进行相关试验研究。

1 电机结构与工作模态

基于不对称振动模态的直线超声波电动机的结构如图1所示。电机由一个杆式螺母、螺杆和压电陶瓷片组成，定子由杆式螺母和二片矩形压电陶瓷片构成。压电陶瓷片作为换能器件，通过胶层与杆式螺母紧密地粘接成一体。在交变激励电压的作用下压电陶瓷片被激发应变，并将应变能传递给杆式螺母，激发出定子相应的振动模态，从而使得定子驱动端上的质点产生椭圆运动。该椭圆运动加上定子、螺杆间的摩擦力，就会推动螺杆进行旋转运动，并最终转换为直线运动输出。

图2为该电机定子所利用的两个弯曲振动模态。从图1可以看出，定子为一个沿X'轴对称，沿Y'轴不对称的结构。工作模态1为一个左右弯曲振动模态，如图2(a)所示。工作模态2为一个前后弯曲振动模态，如图2(b)所示。由于定子结构的不对称性，其工作模态1的共振频率要小于工作模态2的共振频率。两个工作模态的频率不相等是该类电机的特点。

图1 直线超声波电动机结构图

图2 电机定子的工作模态

2 电机运动分析

该电机可以使用一相正弦交变电压驱动其工作，也可以使用一相正弦和一相余弦交变电压驱动其工作。当对其中一片压电陶瓷片施加合适频率的正弦交变电压，将激励出定子的两个工作模态，使定子上的驱动点产生椭圆运动，推动螺杆沿一个方向旋转直线运动。如果是对另一片压电陶瓷片施加正弦交变电压，同样能激励出定子的两个工作模态，此时将推动螺杆朝相反方向旋转直线运动。假如对两片压电陶瓷片分别施加合适频率的正弦和余弦交变电压，也将激励出定子的两个工作模态，驱动螺杆沿一个方向旋转直线运动。切换交变电压的相位，即可改变螺杆的运动方向。

2.1 电机受单相激励时的运动机理

假设电机定子的一阶弯曲振动工作模态频率为ω，O1为定子轴线与上端面的交点，S为定子端面上的任一驱动质点。当对A相压电陶瓷片施加电压sin ωt激励时，两个工作模态都会响应，但两者响应存在相位差φ。工作模态1响应时的电机定子变形简图如图3所示，在忽略定子其他模态和阻尼影响的情况下，O1点在X方向的位移响应:

端面转动角位移响应:

式中:W0和β0分别表示O1点横向位移和转动角位移的最大值。

图3 工作模态1响应时定子变形示意图

在微小变形情况下，定子弯曲变形符合平面假设。如图3所示，S点在X、Z方向的位移响应可以表示:

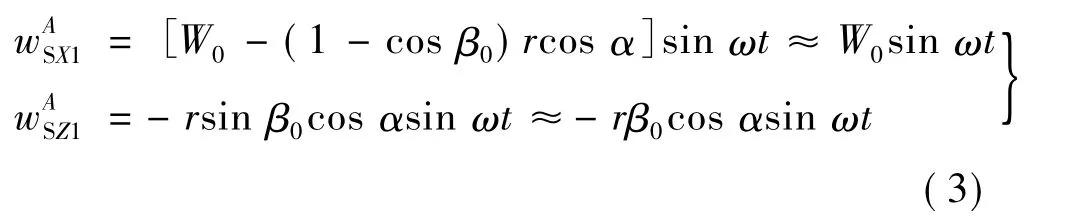
工作模态2响应时，引起S点在Y、Z方向的位移响应:

因此，S点在X、Y和Z方向的位移响应可以表示:

将S点在X、Y的位移沿径向r和切向τ分解，如图3所示，因此有:

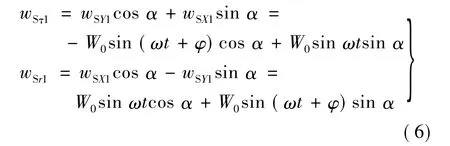
因此有:

由式(7)可见，当只有A相陶瓷片受激振时，S点的运动轨迹为一斜椭圆。

2.2 电机受两相激励时的运动机理

在对A相压电陶瓷片施加电压sin ωt激励的同时，对B相压电陶瓷片施加电压cos ωt激励。激励电压cos ωt引起S点在X、Y和 Z方向的位移响应可同理求出:

因此，当A、B两相同时激振，S点在X、Y和Z方向的位移响应:

将S点在X、Y的位移沿径向r和切向τ分解:

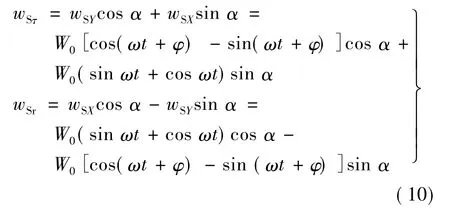
因此有:

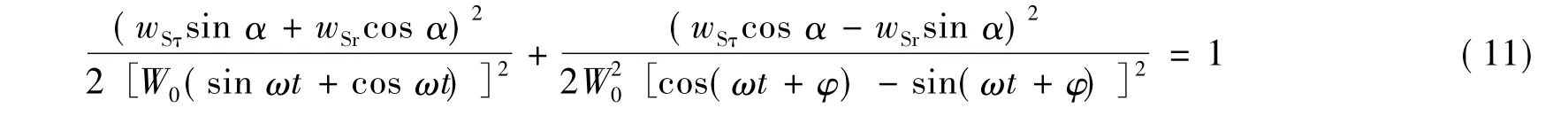
由式(11)可以看出，当A、B两相陶瓷片同时受激振时，S点的运动轨迹为一斜椭圆。

3 有限元数值分析

对直线超声波电动机定子建立ANSYS有限元模型，如图4所示。定子金属弹性体采用SOLID45单元，压电陶瓷采用SOLID5单元。定子金属弹性体材料是黄铜，密度为8 800 kg/m3，弹性模量为90 GPa，泊松比为0.33。陶瓷片的材料是PZT－8，密度为7 650 kg/m3，泊松比为0.31，其刚度矩阵、压电应变矩阵和介电常数矩阵分别:

图4 电机定子有限元模型

计算得定子的两个弯曲振动模态频率分别为134.87 kHz和140.45 kHz。并对定子进行了谐响应分析，以分析电机在不同驱动频率下单相和两相电压激励时驱动质点的运动轨迹。

图5分别为驱动频率为133.8～140.3 kHz时单独激励A相和B相时驱动点S的运动轨迹，所施加的电压为20 V，箭头为驱动点的旋转方向。从仿真结果可以看出，只对其中一相压电陶瓷片施加合适的激励电压，也能激发出定子的两个工作模态，验证了电机受单相激励时的运动机理分析。当激励另一相压电陶瓷片时，驱动点的运动方向将改变，同时螺杆的运动方向也会改变。

图5 电机单相激励时驱动点S的运动轨迹

图6 电机两相激励时驱动点S的运动轨迹

图6(a)为驱动频率为133.8～140.3 kHz时对A、B相分别施加正弦、余弦交变电压时，驱动点S的运动轨迹，所施加的电压为20 V，箭头为驱动点的旋转方向。从图中可看出，合适的驱动频率能激励出驱动点较大的振幅。图6(b)为切换交变电压的相位后驱动点S的运动轨迹。切换相位后，能改变驱动点的运动方向，同时也改变了螺杆的运动方向。该仿真验证了电机受两相激励时的运动机理分析。

4 样机试验研究

根据有限元设计结果，制作了样机，如图7所示。其中，压电陶瓷片尺寸为0.2 mm ×1.3 mm ×6 mm，定子外形尺寸为1.72 mm ×1.72 mm ×6 mm，螺杆长 12 mm。利用PSV－300和PCV－Z－040－F多普勒激光测振仪测试了电机定子的振动模态，其幅频响应曲线和一阶弯曲振型如图8所示。图中实线和点划线分别为A相和B相幅频响应曲线，两个空间上正交的弯振模态的频率分别为132.3 kHz和130.1 kHz。实际测量的弯曲振动模态频率比有限元计算频率偏低，这主要是由于有限元建模的尺寸、材料与实际电机的加工尺寸、材料属性存在偏差，以及有限元模型中对不同材料公共面的公共节点的位移认为是完全连续的，这样增加了定子的计算刚度，因此使得计算的模态频率偏高。相对于大尺寸电机来说，微小型电机有限元建模与实际情况的偏差导致的计算误差更大。本文分别以共振频率为激励频率、20 V激励电压，对A、B两相进行定频试验，定子端面质点一阶弯振振幅分别为 0.25 μm、0.18 μm，该试验结果与有限元仿真计算结果接近。利用信号发生器(Tektronix AFG3022)与功率放大器(HFPA－41)为电机供电，驱动频率为131.9 kHz，激励电压为40 V时，测得电机单相激励时的空载速度为3.9 mm/s，两相激励时的空载速度为4.9 mm/s。

图7 直线超声波电动机实物图

5 结 语

本文介绍了一款微型直线超声波电动机的研制。该电机利用两个不对称的弯振模态工作，可以实现单相驱动以及两相驱动。建立了定子的运动学模型，分析了在单相驱动和两相驱动下，驱动质点的运动轨迹，并推导出其椭圆运动轨迹方程。利用有限元对定子驱动点的运动轨迹进行了仿真和分析，检验了电机运动机理分析的正确性。制作了直线超声微电机原理样机，其定子尺寸仅为1.72 mm×1.72 mm×6 mm，在驱动频率为131.9 kHz、激励电压为40 V时，电机单相、两相激励的空载速度分别为3.9 mm/s、4.9 mm/s。毫米级微型直线超声波电动机在微型机器人、微型飞行器、微型医疗设备、微型照相聚焦镜头等领域中有广阔的应用前景，今后还需在电机性能的提高、新原理样机的研发、电机设计模型修正方面做进一步的研究。

［1］ 赵淳生.超声电机技术与应用［M］.北京:科学出版社，2007.

［2］ Kanda T，Makino A，Ono T，et al.A micro ultrasonic motor using a micro － machined cylindrical bulk PZT transducer［J］.Sensors and Actuators，2006，A127:131 －138.

［3］ 李朝东，何晓菁.卧式板型直线超声电机的微型化［J］.光学精密工程，2010，18(4):887 －892.

［4］ 周铁英，鹿存跃，陈宇.毫米压电微电机的发展与应用［J］.微特电机，2005(12):41－44.

［5］ Leea W H，Kang C Y，Paik D S，et al.Butterfly － shaped ultra slim piezoelectric ultrasonic linear motor［J］.Sensors and Actuators，2011，A168:127 －130.

［6］ Watson B，Friend J，Yeo L.Piezoelectric ultrasonic resonant motor with stator diameter less than 250 μm:the Proteus motor［J］.Journal of Micromechanics and Microengineering，2009，19(2):1 －5.

［7］ Morita T，Kurosawa M K，Higuchi T.A cylindrical shaped microultrasonic motor utilizing PZT thin film(diameter 1.4mm and L5.0mm stator transducer)［J］.Sensors and Actuators，2000，A83:225－230.

［8］ Cagatay S，Koc B，Uchino K.A 1.6 － mm，metal tube ultrasonic motor［J］.IEEE Transactions on Ultrasonics，Ferroelectrics，and Frequency Control，2003，50(7):782 － 786.

［9］ Dong Shuxiang，Lim Siak P，Lee Kwork H，et al.Piezoelectric ultrasonic micromotor with 1.5 mm diameter［J］.IEEE Transactions on Ultrasonics，Ferroelectrics，and Frequency Control，2003，50(4):361－367.

［10］ 周铁英，张凯，陈宇，等.1 mm圆柱式超声电机的研制及在OCT内窥镜中的应用［J］.科学通报，2005，50(7):713－716.

［11］ Henderson D A.Ultrasonic Lead Screw Motor.US Patent 2005/0052094 A1.2005.