多刚体滑模姿态协调控制

高 岱，吕建婷，王本利

（1.哈尔滨工业大学卫星技术研究所，150080 哈尔滨;2.黑龙江大学 数学科学学院，150080 哈尔滨）

多刚体滑模姿态协调控制

高 岱1，吕建婷2，王本利1

（1.哈尔滨工业大学卫星技术研究所，150080 哈尔滨;2.黑龙江大学 数学科学学院，150080 哈尔滨）

本文研究了多刚体分布式姿态协调控制问题.基于图论和滑模控制理论，针对修正罗德里格参数描述的姿态跟踪控制系统，设计了滑模姿态协调控制律.首先引入图拉普拉斯矩阵，采用Lyapunov稳定性分析方法设计了滑模面.然后在干扰存在时设计了滑模姿态控制算法，并在转动惯量不确定存在时研究了控制算法的鲁棒性.最后对给出的算法进行了数值仿真，其结果验证了所提出的多刚体滑模姿态协调控制算法的可行的、有效的.

分布式控制;姿态协调;滑模控制

多刚体分布式姿态协调控制问题是当前的一个研究热点，已引起国内外的广泛关注.典型的姿态协调控制目标是实现姿态同步和跟踪，保证闭环系统的全局渐近稳定性.与传统的集中式控制相比，分布式控制具有规模灵活、鲁棒性强和便于维护等优点.

常用来研究一阶或二阶积分器系统的图论方法最近已被用来分析多刚体的姿态协调控制问题.图论中的拉普拉斯矩阵以及它的谱特征在一致性收敛分析中有重要的作用.与一阶和二阶积分器系统相比，非线性的多刚体姿态协调控制有着更实际的应用价值，同时也存在新的技术难题.文献［1］在拓扑结构为无向图时，进行了没有绝对角速度和相对角速度反馈的姿态同步和跟踪控制算法研究.文献［2］考虑三种不同情况，在无向图和有向图情形进行了分布式姿态同步问题研究.文献［3］考虑编队航天器的相对轨道和姿态控制问题，设计了分布式姿态控制律.文献［1－3］均使用四元数对姿态进行描述.文献［4－6］采用修正罗德里格参数(MRP)进行姿态描述，进行了姿态协调控制问题的研究.文献［4］分别考虑输入受限、无角速度反馈及时变参考信号，给出了多刚体分布式姿态控制律，实现了姿态同步.文献［5］研究了多刚体分布式姿态同步和跟踪问题.文献［6］在控制律中引入图拉普拉斯矩阵，给出了主从式的多刚体姿态协调控制算法.除了研究全状态反馈和输出反馈姿态协调控制问题，文献［7－10］给出了存在干扰和转动惯量不确定时的分布式姿态控制算法.文献［7］给出了鲁棒分布式姿态调节协调控制算法.文献［8］针对网络Euler-Lagrange系统，给出了分布式自适应一致性算法.文献［9］考虑了干扰抑制、转动惯量不确定问题，针对主从式航天器编队，进行了姿态控制的研究.文献［10］给出了鲁棒姿态协调控制律，在干扰和转动惯量不确定存在时保证了闭环系统的全局渐近稳定性.

本文首先给出刚体动力学方程以及由修正罗德里格参数描述的运动学方程，以及误差方程和Euler-Lagrange形式的等价方程.然后介绍了图论的相关知识.之后针对多刚体的姿态协调控制问题，考虑网络拓扑是无向的情况，在干扰和转动惯量不确定存在时，采用滑模控制方法，设计了滑模面和分布式滑模姿态协调控制律.本文滑模面的选取没有采用一般形式，在设计时考虑了相对姿态.通过Lyapunov稳定性分析，证明闭环系统是全局渐近稳定的.最后对提出的算法进行了数学仿真验证，结果表明了所设计的控制算法是行之有效的.

1 数学模型

1.1 刚体姿态运动方程

考虑第i个刚体姿态运动的动力学方程为

由MRP描述的刚体非线性运动学方程为

1.2 误差系统

定义误差姿态δσi，即编队中的每个刚体的当前姿态σi与期望姿态σdi间的偏差，和误差姿态角速度 δωi为

这里 ωdi为期望姿态角速度，R(δσi)=R(σi)R(σdi)T为期望坐标系到本体坐标系的转换矩阵.这里有

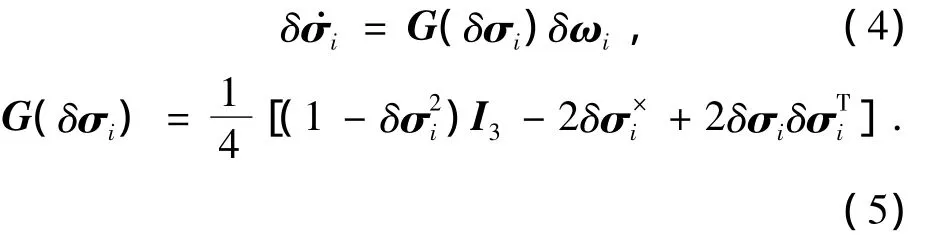
由式(1)、(2)和(4)得到刚体误差动力学方程为

定义 Fi=Fi(δσi)=G(δσi)，将(4)代入(6)整理得到如下方程:

方程(7)具有如下两个重要的性质:

2 图论基础

图Gn是由非空的节点集N={1，2，…，n}与边集E∈N×N组成，可记为Gn=(N，E).

有向图，边是有向的，边(i，j)∈E表示第j个节点能够得到第i个节点的信息，反之不必成立.

无向图，边(i，j)表示第i个节点和第个j节点能够互相得到对方的信息，无向图是有向图的一个特例.

图Gn的邻接矩阵A=［aij］∈Rn×n定义为

对于带权的邻接矩阵A中的元素aij定义为:当(j，i)∈E时，aij＞ 0，否则aij=0.图Gn的拉普拉斯矩阵L= ［lij］∈ Rn×n定义为

当图为无向图时，拉普拉斯矩阵L为对称半正定的.

如果无向图中任意两个节点之间都有一条边将其连通，则称该图是连通的.

3 姿态协调控制律设计

下面基于图论和滑模控制方法研究多刚体姿态协调控制.首先采用Lyapunov稳定性分析方法设计了滑模面.然后在干扰存在时设计了滑模姿态控制算法，并在转动惯量不确定存在时研究了控制算法的鲁棒性.刚体间的通信拓扑用图Gn来表示，这里考虑网络拓扑是无向的情况.为了说明下面的结果，令Ni⊂{1，…，n}{i}表示与刚体i通信的所有刚体的集合.

3.1 滑模面的设计

定理1 选择滑模面si为

当 si→ 0，无向图被连通时有 σi→ σdi，σi(t)－ σj(t)→σdij，ωi→ωdi，ωi(t)－ωj(t)→ωdij，t→∞.这里ki为大于0的标量，aij是图Gn的邻接矩阵A的元素，σdij和ωdij分别为期望的相对姿态和相对姿态角速度.

证明 选取Lyapunov函数

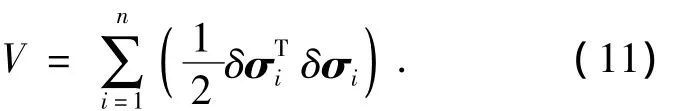
计算V对时间t的导数，得到

因为(L⊗I3)是半正定的，当(L⊗I3)δσ→0，有 Lδσ1→ Lδσ2→ Lδσ3，这里 δσ1，δσ2，δσ3∈Rn.当无向图连通，有 δσi→ δσj.因此可以得到δσi(t)→ δσj(t)→ 0，t→ ∞ 时，即 σi→ σdi，σi(t)－σj(t)→σdij，进一步有ωi→ωdi，ωi(t)－ωj(t)→ ωdij.

3.2 滑模控制律设计

假设1 干扰是有界的‖di‖≤dmax.

定理2 考虑由式(4)、(6)描述的系统，在干扰存在下，设计滑模控制律ui为

其中ksij为三维对角正定阵Ksi对角线上的元素，满足 Ksil＞ 2dmax，l=1，2，3.如果无向图被连通，则有σi→σdi，σi(t)－σj(t)→σdij，ωi→ωdi，ωi(t)－ ωj(t)→ ωdij，当 t→ ∞.sgn(s)=［sgn(s1)sgn(s2)sgn(s3)］T，sgn(sl)为符号函数，aij是邻接矩阵A的元素.

证明 对第i个刚体，选取Lyapunov函数

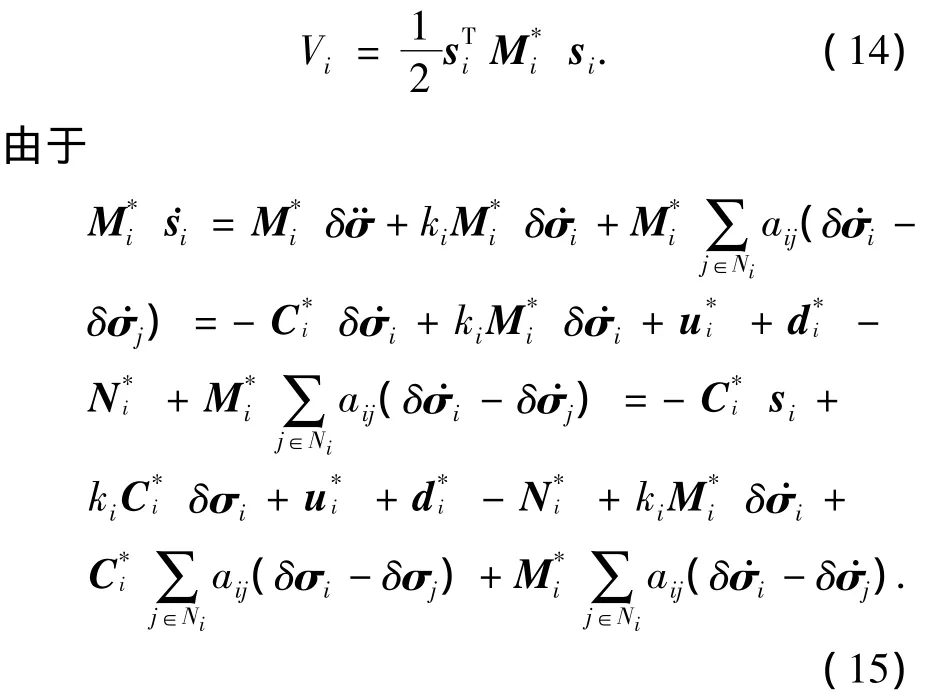
计算Vi对时间t的导数，得到

考虑性质2，并将控制律代入(16)，得

当ksil＞2dmax|时，有＜0.

在实际中，由于惯性的存在、控制受限及各种非理想因素，滑模运动存在抖振，这里用饱和函数代替符号函数来减小抖振，饱和函数定义如下

这里δ＞0.

3.3 鲁棒性研究

设计滑模控制器ui为

ksil＞|Δg|il，如果无向图是连通的，对于式(4)、(6)描述的系统，有σi→σdi，σi(t)－σj(t)→σdij，ωi→ωdi，ωi(t)－ ωj(t)→ωdij，当t→∞.

这里

证明 对第i个刚体，选取Lyapunov函数

计算Vi对时间t的导数，得到

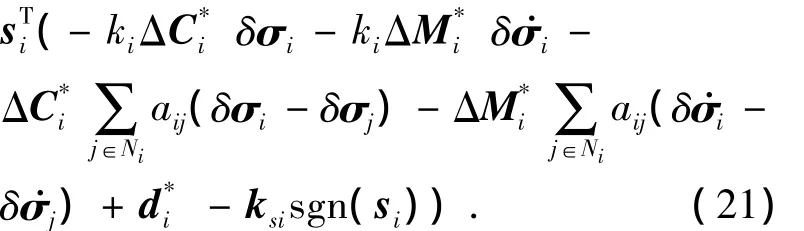
当条件ksil＞|Δgil|满足时，可以看出，当有＜0成立.类似的，可以得到σi→σdi，σi(t)－σj(t)→ σdij，ωi→ωdi，ωi(t)－ ωj(t)→ ωdij，当t→∞.

4 数学仿真

为验证本文所提出的控制算法的可行性和有效性，考虑6个刚体组成的系统进行数学仿真验证，通信拓扑如图1所示.

图1 6个刚体间的拓扑关系

简单起见，选取仿真参数如下所示.刚体的转动惯量为

初始姿态和姿态角速度为

期望的角速度为

和 σdi= ［0 0 0］T.

三轴干扰力矩为

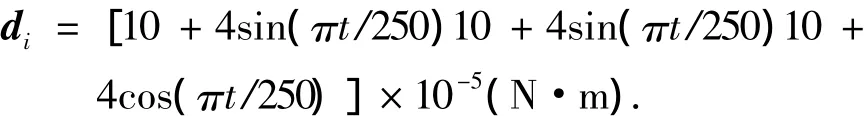
滑模控制器参数选取为

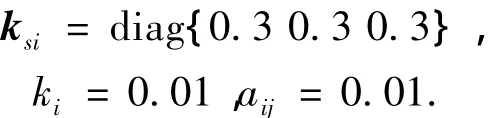
数学仿真结果如图所示.第1，3，5个刚体的姿态σi、姿态角速度ωi和控制输出力矩ui变化曲线分别如图2～4所示.由仿真结果可以看出，干扰存在时，控制方案能很好地完成多刚体的姿态控制任务，实现了控制目标，保证了闭环系统的全局渐近稳定性.

图2 MRP变化曲线

图3 姿态角速度变化曲线

图4 控制力矩变化曲线

当转动惯量增大15%时，第1，3，5个刚体的姿态、姿态角速度曲线分别如图5、6所示.

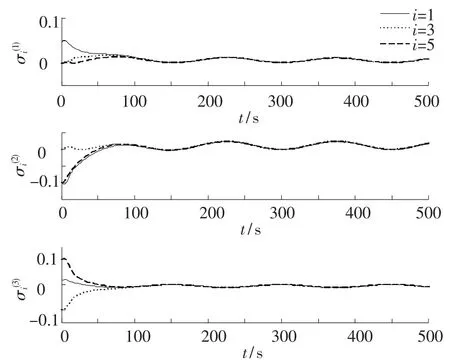
图5 MRP变化曲线

图6 姿态角速度变化曲线

由图可以看出，所设计的滑模控制方案在干扰存在时能够较好地完成多刚体的姿态控制任务，对转动惯量参数变化具有鲁棒性.

5 结论

本文研究了多刚体的分布式姿态协调控制问题.针对MRP描述的姿态跟踪控制系统，给出了多刚体的滑模姿态协调控制算法.通过Lyapunov分析证明了多刚体的全局渐近稳定性.仿真结果表明所设计的控制方案很好地实现了多刚体的姿态同步和跟踪.

［1］ABDESSAMEUD A，TAYEBI A.Attitude synchronization of a group of spacecraft without velocity measurements［J］.IEEE Transactions on Automatic Control.2009，54(11):2642－2648.

［2］REN Wei.Distributed attitude alignment in spacecraft formation flying［J］.International Journal of Adaptive Control and Signal Processing.2007，21(2－3):95－113.

［3］REN Wei.Formation keeping and attitude alignment for multiple spacecraft through local interactions［J］.Jour-nal of Guidance，Control and Dynamics.2007，30(2):633－638.

［4］REN Wei.Distributed attitude synchronization for multiple rigid bodies with Euler-Lagrange equations of motion［C］//Proceedings of the 46th IEEE Conference on Decision and Control.New Orleans，LA，USA:［s.n.］，2007，2363－2368.

［5］REN Wei.Distributed cooperative attitude synchronization and tracking for multiple rigid bodies［J］.IEEE Transactions on Control Systems Technology.2010，18(2):383－392.

［6］DIMAROGONAS D V，TSIOTRAS P，KYRIAKOPOULOS K J.Leader—follower cooperative attitude control of multiple rigid bodies［J］.Systems ＆ Control Letters，2009，58(6):429－435.

［7］JIN Erdong，JIANG Xiaolei，SUN Zhaowei.Robust decentralized attitude coordination control of spacecraft formation［J］.Systems＆ Control Letters，2008，57(7):567－577.

［8］MIN Haibo，SUN Fuchun，WANG Shicheng，LI Hongbo.Distributed adaptive consensus algorithm for networked Euler-Lagrange systems［J］.IET Control Theory and Applications，2011，5(1):145 －154.

［9］YUAN Changqing， LI Junfeng， WANG Tianshu，BAOYIN Hexi，Robust attitude control for rapid multitarget tracking in spacecraft formation［J］.Applied Mathematics and Mechanics，2008，29(2):185 －198.

［10］LIANG Haizhao，WANG Jianying，SUN Zhaowei.Robust decentralized coordinated attitude control of spacecraft formation［J］.Acta Astronautica，2011，69(5 －6):280－288.

［11］SLOTINE J-J E，LI Weiping.Applied nonlinear control［M］.Englewood Cliffs，New Jersey:Prentice Hall，1991:123.

Sliding mode coordinated attitude control for multiple rigid bodies

GAO Dai1，LU Jian-ting2，WANG Ben-li1

(1.Research Center of Satellite Technology，Harbin Institute of Technology，150080 Harbin，China;2.School of Mathematical Science，Heilongjiang University，150080 Harbin，China)

The problem of distributed coordinated attitude control for multiple rigid bodies is addressed in this paper.Based on graph theory and sliding mode control theory，a sliding mode coordinated attitude control law aiming at the attitude tracking control system described by the Modified Rodrigues Parameters is proposed.First the sliding surface is designed by introducing graph Laplacian matrix and using Lyapunov stability analysis method.Then the sliding mode attitude control algorithms for multiple rigid bodies with external disturbances are designed，and the robustness of the control algorithm is studied in the presence of uncertainty inertia.Finally，numerical simulations of the algorithms are given.The results show that the sliding mode coordinated attitude control algorithm for multiple rigid bodies is feasible and effective.

distributed control;attitude coordination;sliding mode control

V448.2

A

0367－6234(2012)09－0034－06

2011－07－16.

高 岱(1974—)男，博士;

王本利(1944—)男，教授，博士生导师.

高 岱，mackingtosh@gmail.com.

(编辑 苗秀芝)