复杂结构振动响应预示的能量方法

赵 阳，王 坤

（哈尔滨工业大学航天学院，150001 哈尔滨）

复杂结构振动响应预示的能量方法

赵 阳，王 坤

（哈尔滨工业大学航天学院，150001 哈尔滨）

针对复杂结构的振动响应分析，利用弹簧质量系统对模糊结构进行建模，建立了带有附加模糊结构的杆和梁的运动控制方程，在此基础上，进一步推导了能量密度的控制方程，以能量密度为输出响应进行了结构振动的仿真分析.仿真结果显示，模糊结构对结构振动能量密度响应的影响在其固有频率附近最大，这种影响通过模糊结构产生的随频率变化的等效质量实现，在模糊结构固有频率以内的低频域，等效质量为正，降低了结构振动的能量密度响应，在高于固有频率的频域内，等效质量为负值，使得结构的能量密度响应增大.

模糊结构;能量密度;振动响应预示

各种工程结构的振动响应分析一直是很重要的问题，有限元法作为成熟的技术，在振动分析领域得到了广泛应用.由于有限元法的计算成本会随着频率的升高而增大，因此并不适用于高频领域.为解决高频域的声振预示问题，Lyon［1－2］提出了新的振动分析方法——统计能量分析.自此，基于能量的振动分析方法得到了长足发展，Nefske和Sung［3］在分析梁结构的振动时，利用能量密度作为变量得到了结构振动的另一种形式的控制方程——能量密度控制方程，此方法经过 Bouthier［4－5］和 Cho［6］等人的推广，通过与有限元技术结合，发展成为实用的能量预示方法，被称为能量有限元法.Xiaoyan Yan针对复合材料层合板结构推导了能量密度控制方程［7］.Sung-Min Lee则利用能量有限元法与周期理论相结合，计算了旋转体结构的响应并进行了实验验证［8］.与有限元技术的结合使其可以得到比统计能量分析更为精细的结果，另一方面，由于以平均化的能量密度为变量，大大减小了计算成本.此预示方法在结构振动分析领域具有很好的应用前景与实用价值.

针对实际结构进行声振响应分析时，结构的建模面临着一些困难.这是由于实际工程结构一般比较复杂，在主结构之外还有许多附加结构，这些附加结构在一定程度上改变了主结构的振动响应，但由于难以建立精确模型，传统的处理方法经常忽略这些内部结构，或者作为固结的附加质量处理.为了研究附加结构对主结构振动响应的影响，Soize［9］将可建模的主要部分称为主结构，与主结构相连的附加结构定义为模糊结构，研究了模糊结构对于主结构的阻抗特性.Pierce等［10］在对Soize的理论进行简化的基础上，从声振角度分析了附加结构的影响.本文将模糊结构理论引入能量预示方法，从振动响应的能量密度出发，以杆和梁结构为研究对象，研究了带有附加模糊结构的杆和梁振动的能量密度响应的特点.

1 杆结构的振动建模

模糊结构的精确建模是一个十分复杂的问题，从动力学角度来看，模糊结构的组成要素为质量、刚度和阻尼，因此可以利用弹簧质量系统进行建模.由此，图1所示的杆结构满足的动力学方程为［11］

式中:F为杆内力，j为虚数单位，x表示杆的坐标，ω为激振频率，m'表示弹簧质量系统的质量，ω0表示弹簧质量系统的自然频率，E为杆的弹性模量，S为截面积，vs表示杆振动的速度.

图1 带弹簧质量系统的杆或梁

由方程(1)和方程(2)，以速度为变量的杆的运动控制方程

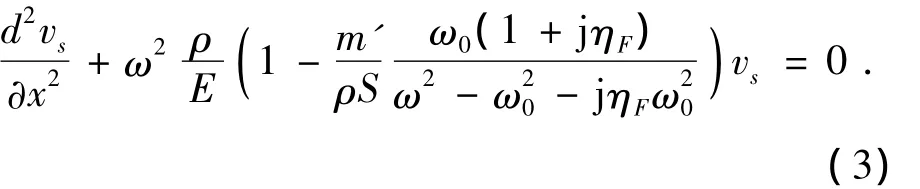
方程的通解为

式中:U(x，t)表示位移，t表示时间，A和B为待定系数，由边界条件确定.

式中:ν=ω/ω0为激振频率与主结构杆的固有频率之比，k0为主结构杆的纵向振动波数.

杆运动的势能和动能分别为

则杆运动的总能量为

杆内力的功率

对变量进行平均，可以得到功率与能量密度的关系式

利用能量平衡方程［4］，可以得到带模糊结构的杆的能量密度控制方程为

式中:c为杆结构的波群速度，η为阻尼系数，e为杆中时间和空间平均的能量密度.此控制方程在形式上与文献［3］中无附加结构杆的能量密度控制方程相同，需要注意的是，由于此控制方程在推导过程中考虑了附加模糊结构的影响，式(5)中的波速不同于文献［3］中的波速，它引入了附加模糊结构的质量，并直接影响到了能量密度响应.

2 梁结构的振动建模

同样利用图1所示结构，梁受到模糊结构的作用力为

式中:w为梁的横向振动位移，Z为弹簧质量系统的基础激励阻抗.

则运动方程变为

式中:kb0为主结构梁的弯曲振动波数.

得到带模糊结构的梁的运动控制方程:

式中:ζ=ω/ω0为激振频率与主结构梁的固有频率之比，等效波数

Russel给出了具有以上形式的运动控制方程，并指出梁结构与板结构的运动方程具有相同形式［12］.本研究针对梁结构，在此运动方程的基础上推导能量密度的控制方程.

方程通解形式为

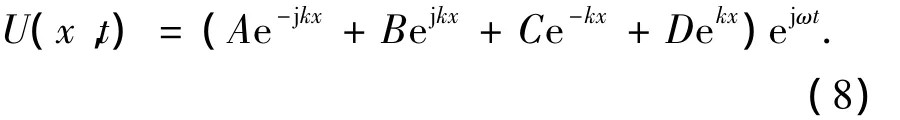
式中:A、B、C和D表示待定系数，通过边界条件确定.

梁中的功率为

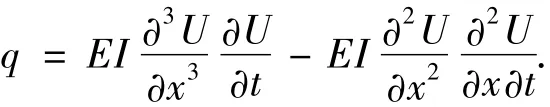
梁结构运动的势能和动能分别为

同样利用能量平衡关系，对变量进行平均化，可以得到功率与能量密度的关系式

及带模糊结构梁的能量密度控制方程

式中:c为梁结构的波群速度，η为阻尼系数，e为梁中时间和空间平均的能量密度.

可以看到，带模糊结构的梁振动的能量密度控制方程与带模糊结构的杆的能量密度控制方程具有相同的形式.并且与简单结构的能量密度控制方程相同的形式，这样，已有的能量控制方程的解法可以直接得到应用.

3 仿真分析

针对附加模糊结构对主结构运动的影响，在模糊结构质量与主结构质量之比为0.01、0.05和0.10时，进行数值仿真，得到了杆和梁结构中点位置波速和能量密度响应随频率的变化.杆弹性模量E=5 000 N/m2，长 L=1 m，阻尼 η =0.01，线密度 ρS=2 300 kg/m梁的抗弯刚度EI=7 200 Nm2，长 L=1 m，阻尼 η =0.01，线密度 ρS=3 200 kg/m.

图2和图3分别显示了带有模糊结构的杆的波速与能量密度响应与频率的关系.由图2，由于模糊结构的存在，杆结构波速c在低频段减小，但幅度较小，随着频率的升高，在接近模糊结构共振频率ω0时，变化幅度变大，并在ω0附近发生急剧变化，波速c由极小值变为极大值，并随着频率的进一步升高而降低，最终趋于无模糊结构杆的波速c0.图3显示杆的能量密度e由于模糊结构的存在，在低频段变大，并随着频率的升高而继续增大，在模糊结构共振频率ω0附近由极大值变为极小值，随后随着频率的升高而回升，逐渐趋向于无模糊结构杆的能量密度响应值e0.模糊结构质量分数大的杆，在达到固有频率之前，波速c减小幅值更大，能量密度e的增加幅值更大，在固有频率之后波速c增大的幅值更大，能量密度e减小的幅值更大.

图2 杆的波速随频率变化图

图3 杆的能量密度随频率变化图

图4和图5是带模糊结构的梁的波速和能量密度响应随频率变化情况.跟杆结构的趋势相似，梁结构的波速c在低频域因模糊结构影响而减小，在频率到达模糊结构固有频率ω0前达到极小值，随后急剧改变达到极大值，随着频率的进一步升高，波速趋向于主结构梁的波速c0，梁的能量密度e则是在低频域逐渐增大，经过ω0后变为极小值，以后继续增大并趋向于e0.模糊结构质量分数大的梁，在达到模糊结构固有频率前，波速c增加的幅值更大，能量密度响应e的减小幅值更大，在固有频率之后波速c减小的幅值更大，能量密度e增加的幅值更大.

图4 梁的波速随频率变化图

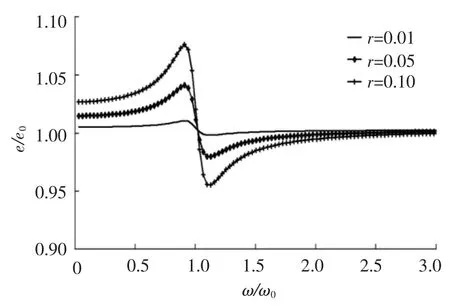
图5 梁的能量密度随频率变化图

4 结论

通过对带有附加模糊结构的杆和梁的振动的能量密度响应分析可以发现，模糊结构的存在引起了主结构的运动控制方程参数的变化，其对杆和梁结构能量密度响应的影响在固有频率附近最大，这种影响通过对波速的改变来实现，结构波速c的增大降低了结构的能量密度响应e，波速的减小则增大了能量密度响应值.波速c的改变反映的是结构等效质量的改变，因此，模糊结构对主结构的影响实际是产生对主结构的等效质量实现的.对于杆和梁结构，以带无阻尼模糊结构的杆为例，利用前文得到的波数表达式，杆的波速为

波速在模糊结构固有频率以内的低频域，随着激振频率的升高，频率比 ν＜1，因此(m'/ρS)/(1－ν2)项为正，且不断增大，对于波速而言，这跟模糊质量m'为正且不断增大产生的效果相同，因此降低了结构振动的能量密度响应，在固有频率之后，频率比ν＞1，在此情况下，模糊结构项(m'/ρS)/(1－ν2)为正，且绝对值不断减小，对波速而言，等效于模糊质量m'为负且绝对值不断减小，这样，主结构振动的能量密度响应相应的增大，随着频率的继续升高，等效质量逐渐减小直至趋近于零.此等效质量作为振动频率的函数，其具体形式是一个难点，目前尚未见有深入研究，需要在未来工作中作进一步探讨.

［1］LYON R H，MAIDANKIK G.Power flow between linearly coupled oscillators［J］.Journal of Acoustic Society of America，1962，34(5):623 －639.

［2］LYON R H，SCHARTON T D.Vibrational energy transmission in a three element structure［J］.Journal of Sound and Vibration，1965，38:253 －261.

［3］NEFSKE D J，SUNG S H.Power flow finite element analysis of dynamic system:Basic theory and application to beams［J］.Transactions of the ASME，1989，111(1):94－100.

［4］BOUTHIER O M，BERNHARD R J.Models of spaceaveraged energetics of plates［J］.AIAA JOURNAL，1992(30)3:616－623.

［5］BOUTHIER O M，BERNHARD R J.Simple models of energy flow in vibrating membranes［J］.Journal of Sound and Vibration.1995，182(1)129 －147.

［6］CHO P E.Energy flow analysis of coupled structures［D］.West Lafayette，School of Mechanical Engineering，Purdue University.1993.

［7］XIAOYAN Y.Energy finite element analysis development for high frequency vibration analysis of composite structures［D］.Michigan:University of Michigan，2008.

［8］LEE Sungmin.Energy finite element method for high frequency vibration analysis of composite rotorcraft structure［D］.Michigan:Univer－sity of Michigan，2010.

［9］SOIZE C A model and numerical method in the medium frequency range for vibro-acoustic predictions using the theory of structural fuzzy［J］.J.Acoust.Soc.Am，1993，94(2)，849 －865.

［10］PIERCE A D，SPARROW V W，RUSSEL D A.Fundamental structural-acoustic idealizations for structures with fuzzy internals［J］.Journal of Vib-ration and A-coustics.1995，117:339 －348.

［11］CREMER L，HECKL M，PETERSSON B A T.Strcuture-Borne Sound［M］.Berlin:Springer，2004.

［12］RUSSEL D A.The theory of fuzzy structures and its application to waves in plates and shells［D］.University Park:Pennsylvania State University，1995.

Vibration response prediction for the complex structures using energy method

ZHAO Yang，WANG Kun

(School of Astronautics，Harbin Institute of Technology，150001 Harbin，China)

Rod and beam with fuzzy structures is modeled using sprung mass system to analyze vibro-acoustic responses of complex structures.Energy density is used as response method to simulate the structural vibration，and the simulation indicates that the fuzzy structures affect the master structure maximally around the natural frequency of the fuzzy structures.The effect acts as a frequency dependent equivalent mass.The equivalent mass is positive under the natural frequency of the fuzzy structure and negative over the frequency.The positive equivalent mass decreases，while the negative one increases the vibration energy density responses.

fuzzy structures;energy density;vibration response prediction

TB123

A

0367－6234(2012)09－0025－04

2011－08－04.

国家自然科学基金资助项目(11072066).

赵 阳(1968—)，男，教授，博士生导师;

王 坤(1985—)，男，博士研究生.

王 坤，alacarte@163.com.

(编辑 苗秀芝)