重型数控机床热误差的分离与建模

崔岗卫，高 栋，姚英学

（哈尔滨工业大学机电工程学院，150001 哈尔滨）

重型数控机床热误差的分离与建模

崔岗卫，高 栋，姚英学

（哈尔滨工业大学机电工程学院，150001 哈尔滨）

为解决重型数控机床热误差严重的问题，提出一种基于线性回归的热误差分离和建模方法.对机床的几何误差与热误差进行分离，得到相应的热误差参数;结合主因素和互不相关等温度传感器优化布置策略，选出相应的热误差关键点;采用线性回归理论进行热误差的建模.在一台型号为TK6920的重型数控落地铣镗床上进行了立柱热倾斜误差补偿实验.结果表明:利用所建立的热误差模型进行补偿，立柱在X和W方向的直线度误差分别由0.45 mm和0.25 mm降到了0.13 mm和0.09 mm，补偿率分别为71%和64%.采用误差补偿技术可降低重型数控机床的热误差，从而提高其加工精度.

重型数控机床;热误差;误差分离;误差建模;误差补偿

数控机床在加工过程中，会因各种误差因素的影响而使机床的加工精度下降，其中热误差占机床总误差的40% ～70%左右［1］，成为影响机床加工精度最主要的因素之一.而重型数控机床因其质量和惯量大，驱动系统所需功率较大，零部件发热较为严重，热误差尤为明显.针对机床普遍存在的热误差现象，国内外很早就进行了研究，目前关于热误差建模的方法主要有理论建模［1－3］和试验建模［4－5］两种.因机床结构、热源形式以及工作状况复杂多样，所以理论建模方法在实际工程中很难应用.试验建模是基于大量的实验数据，假定机床热误差可以看作是机床表面某些关键离散点温度的函数.将机床表面某些点的温度变化量作为输入，机床的热误差作为输出，通过各种理论，比如神经网络［6－9］、多元线性回归［10－11］、灰色理论、时间序列［12］和支持矢量机［13］等方法来建立热误差模型.目前，各种建模方法主要研究的是普通机床，重型数控机床这方面的研究罕见报道.

本文采用试验建模方法，首先对机床的温度和热误差进行大量的测量试验;然后采用有关优化策略筛选用于建模的温度传感器数量和位置;对测量误差进行分离，获得热误差参数;最后利用筛选出的热关键点处的温度变量作为模型输入，分离出的热误差参数作为模型输出，建立热误差模型并进行实验验证.

1 机床温度场及热误差的测量

1.1 温度传感器的初始布置

在机床热误差的补偿中，温度测点的布置是关键和难点.对于温度传感器的初始布置，一般遵循以下原则［14］:1)温度传感器的数量应多于内部热源的数量;2)传感器应尽量靠近热源;3)为获取最佳的传感器数目和位置，初期的测量实验应设置尽量多的测量点，以保证不丢失重要信息;4)最后的选择结果应来自测量数据处理分析和建模预测实验.

对于本文所研究的重型数控落地铣镗床，在综合考虑其结构形式、热源分布等因素的基础上，结合上述原则，如图1所示，在机床上布置了15个温度传感器:θ1－主轴前轴承处滑枕外表面;θ2－W轴油膜处的刮油板;θ3－滑座表面(作为参考温度);θ4－Y轴油膜处刮油板;θ5－Z轴进给丝杠螺母;θ6～θ10:立柱上光栅尺附近均布5个温度传感器;θ11－Y轴进给丝杠螺母;θ12－X轴进给齿轮端盖;θ13－ W轴进给丝杠螺母;θ14－ 液压油;θ15－ X进给电机轴承端盖.

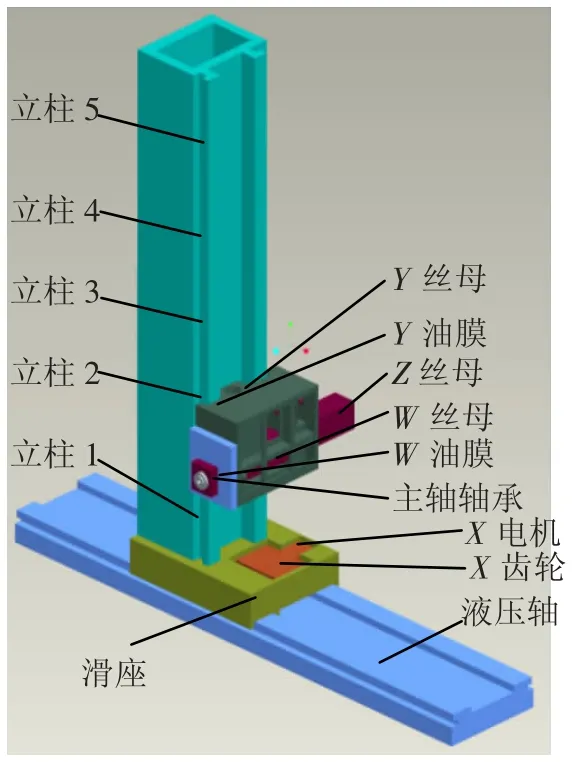
图1 温度传感器初始布置

1.2 温度场的测量

为实时测量并采集温度数据，本文选用铂电阻温度传感器Pt100和15路温度巡检仪.实验结果表明θ5的温度最高，7 h后可达37.1℃，温升高达16.7℃，这是由于该处靠近镗轴的支撑轴承这一热源，当主轴高速旋转时将会产生大量的热，同时该处位于滑枕内部;立柱上的5个温度传感器的测量数据变化最小，这跟立柱远离热源，同时结构尺寸较大，散热条件良好有关;θ1和θ2的温升也较大，因其靠近主轴轴承这一热源;滑枕进给丝杠螺母的温度也较高，因其距离铣轴后轴承这一热源较近;其余温度变化较为缓慢.

1.3 热误差的测量

为模拟机床实际工作生热情况，设计以下实验:主轴转速 650 r/min，X、Y、W 轴进给速度1 000 mm/min，空载，并且机床在没有液压冷却设备的情况下运行7.5 h左右，大约每隔1 h用激光跟踪仪测量一次各进给轴单独运动时的空间坐标误差，同时记下此时各温度传感器的读数.

2 热误差的分离

2.1 误差分离原理

图2所示为机床预热不同时间后，滑枕轴(W轴)定位误差测量结果，图3是机床滑枕热关键点(进给丝杠螺母处，即θ13)不同时刻下对应的温度变化曲线.

图2 不同温度下滑枕定位误差测量结果

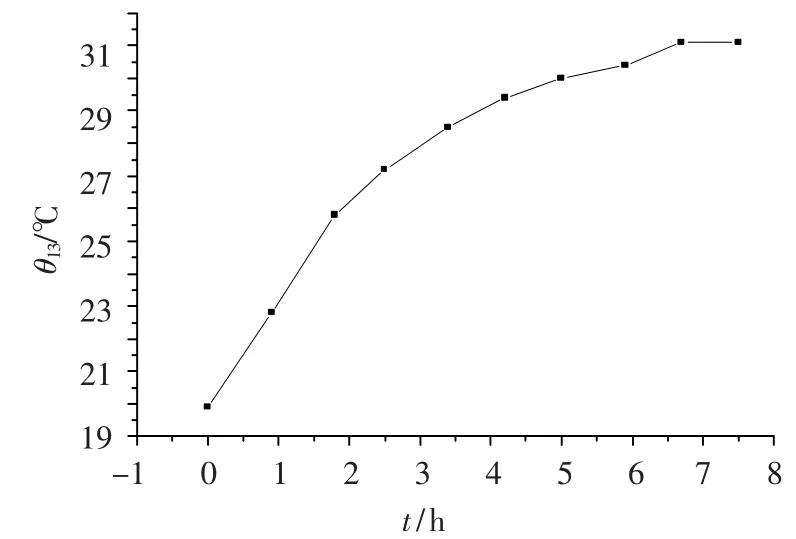
图3 滑枕热关键点处不同时刻的温度(θ13)变化曲线

可以看出，随着机床温度的升高，定位误差也在变大.这就是为什么在实际的切削过程中“螺距误差补偿”的效果并不理想的原因.因其补偿的只是机床冷态时的定位误差，而实际上在加工过程中的定位误差是随着机床温度变化而变化的，故这种既与机床运动坐标有关又与机床温度有关的误差可称为复合误差，要建立复合误差的数学模型，关键是如何将几何误差和热误差进行分离.

复合误差可看作是温度场和坐标位置的函数.从图2中的误差曲线变化规律可以看出，滑枕轴的定位误差曲线在不同温度下外形轮廓基本保持不变，而只是整个曲线的斜率不同.因此这种复合误差元素可分离成两部分:

式(1)中，E(p，θ)为空间复合误差元素，坐标位置p 可以是 x、y、z或 w，温度场向量 θ={dθ1，dθ2，…，dθ15}T;是几何误差元素部分，它只是坐标位置p的函数，可以采用多项式模型拟合计算;为热误差元素部分，是温度场θ和坐标位置p的函数，并且是坐标位置p的线性函数，可按下式计算:

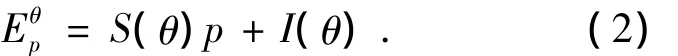
式(2)中I表示截距，S表示斜率.

2.2 重型数控落地铣镗床热误差的分离

针对重型数控落地铣镗床的热误差，分离出了9项坐标误差.由式(2)知，每一项误差都可用直线拟合，对应截距和斜率两个参数，可得18项热误差参数，如表1 ～ 3所示.其中 Ixx、Sxx、Ixy、Sxy、Ixw和Sxw分别表示机床沿X轴运动时X、Y和W这3个方向上的热误差截距和斜率;Iyx、Syx、Iyy、Syy、Iyw和Syw分别表示机床沿Y轴运动时X、Y和W这3个方向上的热误差截距和斜率;Iwx、Swx、Iwy、Swy、Iww和Sww分别表示机床沿W轴运动时X、Y和W这3个方向上的热误差截距和斜率.

表1 X轴热误差参数

表2 Y轴热误差参数

表3 W轴热误差参数

3 热关键点的筛选

一般来说，温度测点选取得越多，模型的预测结果越精确，但是成本也会随之增加，并且往往由于变量间的耦合作用，反而会降低模型精度;相反，若温度测点过少，不能全面的反映机床的温度场信息，在模型中会丢失重要的温度变量.故测温点位置和数量选取正确与否，直接影响热误差模型的精度和补偿效果.

对于机床上温度传感器的优化布置，杨建国等［15］提出了6种策略:1)主因素策略;2)能观测性策略;3)互不相关策略;4)最少布点策略;5)最大灵敏度策略;6)最近线性策略.本文首先利用主因素策略，找到影响热误差的主要温度变量;然后利用互不相关策略，排除相关性较大的冗余温度变量，剩余的作为热误差建模的输入变量.

3.1 主因素策略

通过比较各温度变量与机床热误差参数间相关系数的大小，可找到影响热误差的主要温度变量，即主因素.如表4所示，将每个轴的6个热误差参数看作一组，比较其相关系数的大小，可知X轴热误差的主因素:θ3、θ6、θ11、θ13、θ14和 θ15;Y 轴热误差的主因素:θ3、θ4、θ7、θ8和 θ11;W 轴热误差的主因素:θ1、θ5和 θ13.

表4 测点温度与热误差参数之间的相关系数

3.2 互不相关策略

各温度变量间也可能具有一定的相关性，若将其全部用于热误差建模，由于相关性造成的相互影响，不仅不能提高模型精度，反而会使热误差模型的预测精度下降.各温度变量间的相关性一般采用相关系数来度量.

表5给出了各温度变量间的相关系数.从中可以看出，各温度变量间的相关系数是不同的:对于X、Y、和W轴，其各主因素间的相关系数分别大于0.75、0.85和0.90，说明这些温度变量相关性较强，可从中选出一个作为代表，综合考虑各种因素，分别选 θ15、θ11和 θ13作为 X、Y、和 W 轴的热关键点.

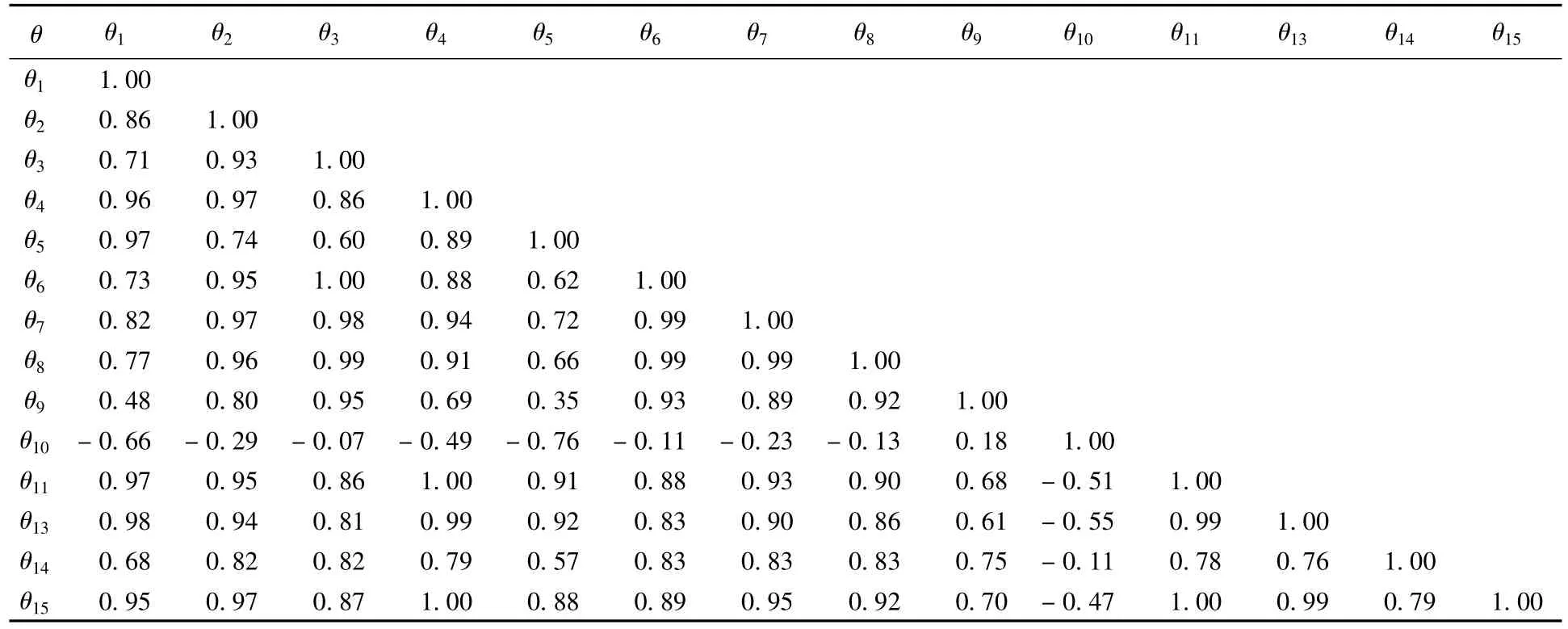
表5 各温度变量之间的相关系数

4 机床热误差的线性回归模型

采用多元回归分析方法进行数控机床热误差建模可以获得较高的预测精度［16］.它是一种用统计方法建立多输入和单输出关系的数学模型，具有计算量小、预测精度高等优点.

以图4如所示的重型数控落地铣镗床X轴定位误差为例，将不同时刻(温度)下热误差的参数即截距Ixx和斜率Sxx绘制成如图5、6所示的曲线.

图4 不同时间的X轴定位误差曲线

图5 不同温度下的X轴定位误差的截距曲线

图6 不同温度下的X轴定位误差的斜率曲线

从图5、6中可以看出，截距Ixx和斜率Sxx可看作温度θ15的线性函数.经拟合计算，并代入式(2)，可得如式(3)所示的X轴定位热误差的数学模型.同理可得如式(4)～(11)所示的其余热误差的模型.

5 实验

为验证所建立热误差模型的正确性，对一台型号为TK6920的重型数控落地铣镗床进行了立柱热误差补偿实验.其补偿原理为西门子数控系统内部的温度补偿模块功能.实验条件为主轴转速650 r/min，进给速度1 000 mm/min，实验时间为6.0～7.5 h，每隔1 h左右进行一次测量，测量仪器为Leica AT901－B激光跟踪仪.实验结果如图7和图8所示，从中可以看出，立柱由于距离主轴箱等发热部分较近，大约6 h后X方向的直线度误差在补偿前高达0.45 mm，Z方向的直线度误差也可达0.25 mm.利用本文所建立的热误差模型进行补偿后，立柱的X向和Z向直线度误差分别降低为0.13 mm和0.09 mm，补偿率分别为71%和64%，说明该方法具有明显的补偿效果.

图7 补偿前后立柱倾斜X向误差对比

图8 补偿前后立柱倾斜Z向误差对比

6 结论

1)对重型数控机床的热误差进行了研究，提出了热误差的分离方法，并对重型数控落地铣镗床的热误差进行分离，得出了18项热误差参数.

2)在理论分析的基础上，结合工程实际经验给出了重型数控落地铣镗床15个温度传感器的初始布置，结合主因素和互不相关等温度传感器优化布置策略，选出了相应的热误差关键点，并采用线性回归理论建立了热误差的数学模型.

3)对一台型号为TK6920的重型数控落地铣镗床进行立柱热误差补偿实验，证明了所建模型的有效性，补偿率可达71%.

［1］WECK M，MC K P.Reduction and compensation of thermal error in machine tools［J］.Annals of CIRP，1995，44(2):589－598.

［2］ZHAO H T，YANG J G，SHEN J H.Simulation of thermal behavior of a CNC machine tool spindle［J］.International Journal of Machine Tools ＆ Manufacture，2007，47:1003－1010.

［3］KIM S K，CHO D W.Real-time estimation of temperature distribution in a ball-screw system［J］.Internatinal Journal of Machine Tools＆ Manufacture，1997，37(4):451－464.

［4］项伟宏，郑力，刘大成，等.机床主轴热误差建模［J］.制造技术与机床，2000，11:12－15.

［5］VELDHUIS S C，ELBESTAWI M A.A strategy for compensation of errors in five-axis machining［J］.Annals of CIRP，1995，44(1):373－377.

［6］CHEN J S Y.Computer-aided accuracy enhancement for multi-axis CNC machine tool［J］.International Journal of Machine Tools＆ Manufacture，1995，35(4):593－605.

［7］杨庆东.数控机床热误差补偿建模方法［J］.制造技术与机床，2000(2):10－15.

［8］王福吉，贾振元，阳江源，等.基于动态模糊神经网络的机床时变定位误差补偿［J］.机械工程学报，2011，47(13):175－179.

［9］KANG Y，CHANG C W，HUANG Y，et al.Modification of a neural network utilizing hybrid filters for the compensation of thermal deformation in machine tools［J］.International Journal of Machine Tools＆ Manufacture，2007，47(2):376－387.

［10］穆塔里夫阿赫迈德，项伟宏，郑力.加工中心主轴热误差实验分析与建模［J］.组合机床与自动化加工技术，2002(9):15－19.

［11］王秀山，杨建国，余永昌，等.双转台五轴数控机床热误差建模、检测及补偿实验研究［J］.中国机械工程，2009，20(4):405－408.

［12］李永祥.数控机床热误差建模新方法及其应用研究［D］.上海:上海交通大学机械与动力工程学院，2007:1－76.

［13］林伟青，傅建中，陈子辰，等.数控机床热误差的动态自适应加权最小二乘支持矢量机建模方法［J］.机械工程学报，2009，45(3):178－182.

［14］LO C H，YUAN J X，NI J.Optimal temperature variable selection by grouping approach for thermal error modeling and compensation［J］.Internatinal Journal of Machine Tools＆ Manufacture，1999，39:1383－1396.

［15］杨建国.数控机床误差综合补偿技术及应用［D］.上海:上海交通大学机械学院与动力工程学院，1998:9－62.

［16］RAMESH R，MANNAN M A.Error compensation in machine tools-a review(part II):thermal Errors［J］.International Journal of Machine Tool＆ Manufacture，2000，40(9):1257－1284.

Thermal error separating and modeling for heavy-duty CNC machine tools

CUI Gang-wei，GAO Dong，YAO Ying-xue

(School of Mechatronics Engineering，Harbin Institute of Technology，150001 Harbin，China)

To solve the problem of thermal error of heavy-duty CNC machine tools，a thermal error separating and modeling approach based on linear regression theory is proposed.Firstly，the thermal errors are separated from geometric error to get thermal error parameters.Secondly，based on temperature sensors optimizing distribution strategies，like main factor strategy and irrelevance strategy，the key points of thermal errors are selected.Finally，a multiple linear regression model is constructed for thermal errors，and an experiment is carried out on a TK6920 heavy-duty CNC floor-type boring and milling machine tool，and the results indicate that the thermal error of column is reduced from 0.45 mm and 0.25 mm to 0.13 mm and 0.09 mm in X and W directions，that is 71%and 64%of thermal error can be compensated with this model.Error compensation technology can reduce the thermal error of heavy-duty CNC machine tools，therefore the manufacturing precision can be improved.

heavy-duty CNC machine tools;thermal error;error separating;error modeling;error compensation

TG502.13

A

0367－6234(2012)09－0051－06

2011－10－24.

国家科技重大专项资助(2009ZX04014－025).

崔岗卫(1980—)，男，博士研究生;

高 栋(1970—)，男，教授，博士生导师;

姚英学(1962—)，男，教授，博士生导师.

高 栋，gaodong@hit.edu.cn.

(编辑 杨 波)