升力式再入飞行器末端能量管理方法

陈 功，解志军，崔乃刚

（1.哈尔滨工业大学航天工程系，150001 哈尔滨;2.空气动力学国家重点实验室，621000 绵阳）

升力式再入飞行器末端能量管理方法

陈 功1，2，解志军2，崔乃刚1

（1.哈尔滨工业大学航天工程系，150001 哈尔滨;2.空气动力学国家重点实验室，621000 绵阳）

以第二代升力式再入飞行器为应用背景，对飞行器再入飞行后的末端能量管理方法进行了深入的研究和分析.在参考航天飞机末端能量管理方法的基础上，分析了TAEM段轨迹参数，优化设计了TAEM段地面轨迹和高度剖面，并进行了纵向和侧向制导律设计.仿真结果表明本文设计的TAEM飞行轨迹满足飞行约束条件，制导方法具有较高的精度和适应性，能满足第二代升力式再入飞行器末端能量管理要求.

末端能量管理;再入飞行器;轨迹优化

末端能量管理(TAEM)是升力式再入飞行器返回过程中的一项关键技术［1］，此段的目的是将无动力滑翔飞行器由再入段终点(TEP)(通常飞行器速度约3Ma、高度约28 km)导引到预备着陆点(ALI)(通常速度约0.5Ma、高度约为3 km).在此飞行段，飞行环境复杂，既要让不同初始能量状态的飞行器满足最终降落的能量要求，又要让飞行器精确对准飞行跑道实现安全降落，这些都对末端能量管理段的轨迹设计提出了很高的要求［2］.早在上世纪80年代，美国的航天飞机首先采用了“混合基准(Hybrid Baseline)”的末端能量管理方案［3］，并取得了巨大的成功，但是这种方案依赖于离线确定的几种标准轨迹，适应性较差.为满足第二代可重复使用飞行器(RLV)的要求，国内 外 很 多 学 者 如 Kluever［4－5］、Schierman［6］、Horneman［7］、Lu P［8－9］等在航天飞机末端能量管理方案的基础上提出了多种在线轨迹规划算法和制导方法，部分学者也结合优化算法求解出满足多种约束要求的末端能量管理段优化轨迹［10］.本文在一种新的轨迹规划算法的基础上实现了末端能量管理段轨迹的优化设计，并采用制导方法进行了仿真验证.

1 末端能量管理段飞行模型

因为TAEM段航程较小，可将地球表面近似看成是平面，忽略地球自转并将再入飞行器看成是1个质点，可以建立如下动力学和运动学模型:

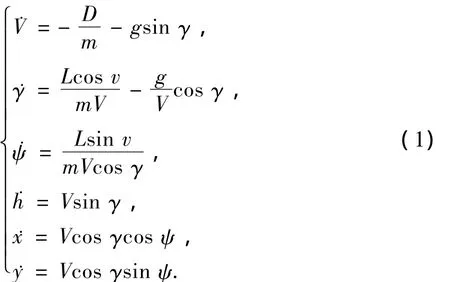
其中:m、V、γ、ψ、x、y、h、D、L 分别为飞行器的质量、飞行速度、弹道倾角、航向角、空间的位置坐标、气动阻力和升力.其中升力和阻力又可表示为

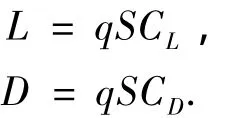
式中:q、S、CL、CD分别为飞行器的动压、特征面积、升力系数和阻力系数.X-33的气动模型已经在美国的AG＆C项目中得到多次应用，因此本文也继续应用X-33的基本参数对本文方法进行仿真验证.为了对气动模型进行简化，X-33阻力系数可由如下的1个曲线函数［7］来表示:

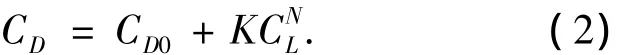
表1给出X-33的零升阻力系数CD0、系数K和N.

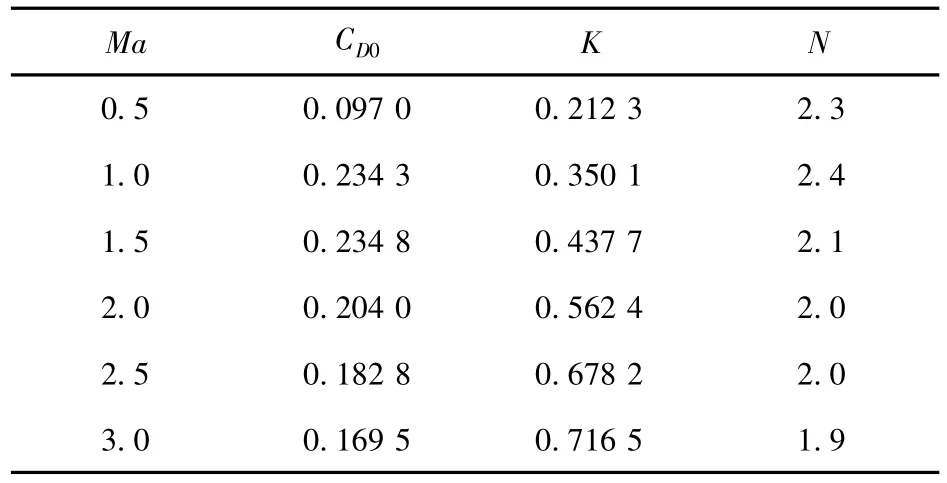
表1 X-33阻力系数

2 参考轨迹设计

如图1所示，参考航天飞机TAEM段参考轨迹划分方法，将TAEM段地面航程分为3个部分:捕获段(acquisition phase)、航向调整段(heading alignment cone，HAC)和预备着陆段(pre-final phase).

在捕获段开始，飞行器通常进行1个圆弧飞行(通常ΔψAT＜10°)，然后沿与HAC段相切的直线飞行到WP1点.在航向调整段，飞行器的飞行轨迹为下降的螺旋线至NEP点(当ΔψHAC＜180°时为直接式进入方式，当ΔψHAC＞180°时为间接式进入方式).到达预备着陆段后，飞行器对航向进行调整以对准机场跑道.当飞行器到达ALI点时，应当满足最终水平降落的各种约束条件.

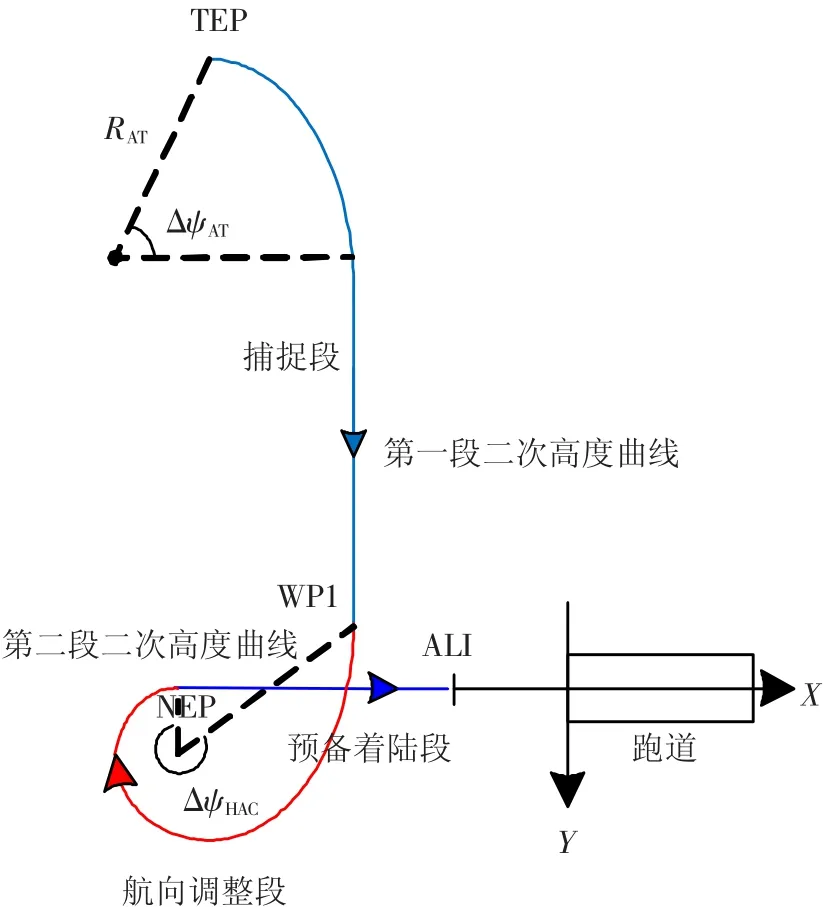
图1 TAEM段地面轨迹

2.1 地面航程预测

由以上分析可知，TAEM段轨迹地面总航程为

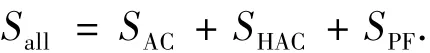
式中SAC、SHAC、SPF分别为捕获段、航向调整段、预备着陆段地面航程.捕获段由圆弧飞行段和直线飞行段组成.而在圆弧飞行段，由于飞行器的速度较大、弹道倾角较小，可将其视为半径不变的圆弧飞行，因此捕获段地面航程预测公式可表示为

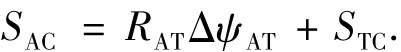
式中STC为捕获端的直线地面飞行距离，转弯半径RAT可近似表示为

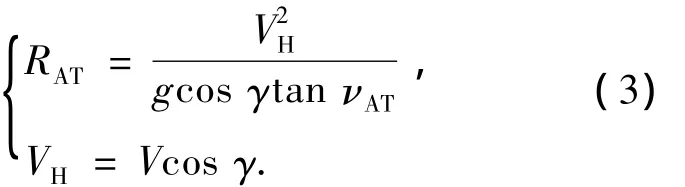
航向调整段螺旋半径公式为

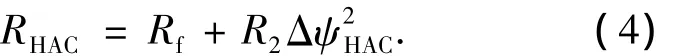
因此HAC地面航程为

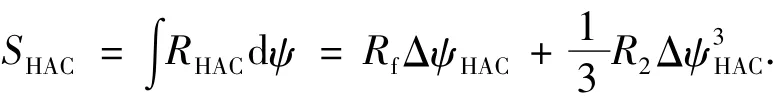
因为预备着陆段是沿机场跑道中线飞行，因此预备着陆段地面航程为

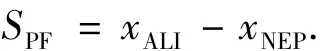
分析几何关系可知，由飞行器的飞行状态信息可以求出ΔψAT和ΔψHAC.因此TAEM段地面航程主要由 νAT、Rf、R2、xNEP这 4 个量决定.

2.2 高度剖面设计

参考航天飞机最终采用的高度剖面形式，可以以地面剩余航程s为独立变量规划高度剖面(由两条连续的高度曲线组成，并让其在WP1点处连续).高度剖面的形式可为

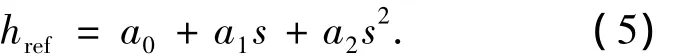
式中s为剩余地面航程，a0、a1、a2为3个待定系数.当s=0时，href=a0，因此可以确定第一条高度曲线中a0=h0，第二条高度曲线中a0=hHAC.对式(5)进行求导可得

同样，考虑到s=0时，第一条高度曲线中a1=tan γ0，第二条高度曲线中 a1=tan γHAC.因为两段地面航程已知，因此两条高度曲线中对应的系数a2为

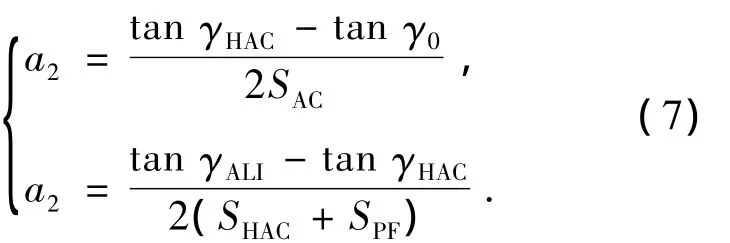
与航天飞机所采用的固定高度剖面相比，本文采用的高度剖面更好的满足了TAEM段的高度、弹道倾角等初始条件.但是从式(5)～(7)可知γHAC和hHAC仍是未知量，但是由两条高度曲线在相切点WP1的连续性可知，hHAC就等于第一条高度曲线的末端高度，因此实际的未知量只有γHAC一个.

2.3 参考控制变量

由捕捉段转弯半径公式(3)可求得

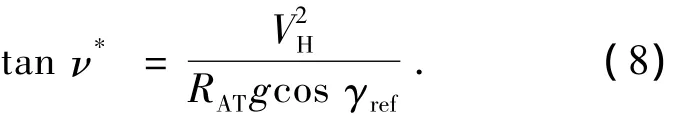
类似上式，可求得HAC段飞行器参考倾侧角公式

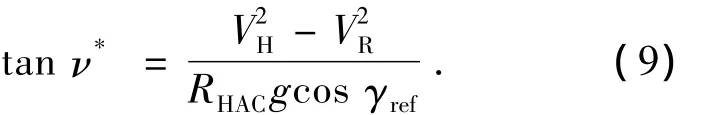
上式中VR是螺旋半径的变化率，由式(4)可得

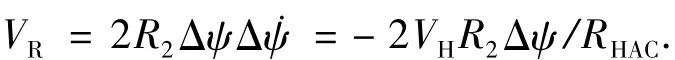
对 tan γref进行求导可得

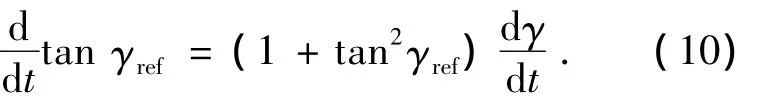
又因为 tan γref=a1+2a2s，所以

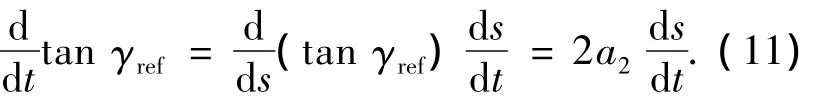
综合式(1)中的第二式、式(10)和(11)，再考虑到剩余航程变化率ds/dt=Vcos γ，可得到参考升力系数的表达式如下:

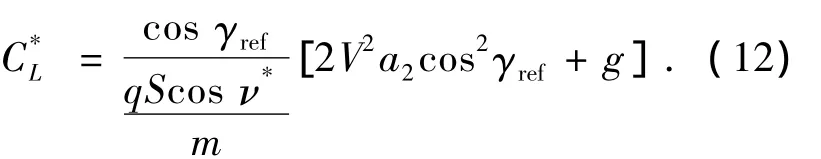
如果由上式求出参考升力系数，并将其代入式(2)可以求得参考阻力系数C.如此，在已知飞行器攻角的情况下可以得到飞行器纵向参考过载指令n，

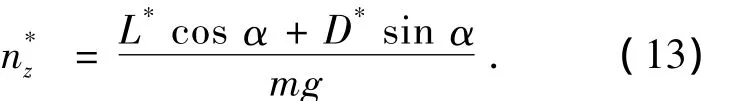
3 轨迹规划算法

由以上分析可知，实际确定地面航程和高度剖面的只有 νAT、Rf、R2、xNEP和 γHAC5 个参数.因为在捕捉段，圆弧飞行段航程占总航程的比例很小，即νAT对飞行器总航程的影响很小，在轨迹设计过程中可以忽略.所以实际TAEM段地面航程和高度剖面由 Rf、R2、xNEP、γHAC4 个量确定.

3.1 第一段轨迹生成

定义高度能量如下:

上式对时间进行求导可得

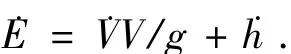
再考虑到式(1)以及ds/dt=Vcos γ，在飞行过程弹道倾角γ较小，忽略小量，上式可变为

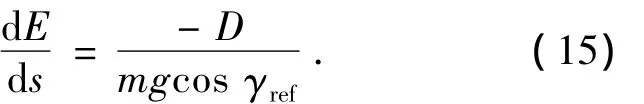
因此从TEP点到WP1点的高度能量可以通过欧拉积分得到

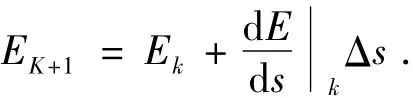
式中Δs=SAC/N，N为积分次数，实际中可取为满足一定精度的常值.如果求出速度、阻力系数、大气密度和参考弹道倾角等4个未知量，就可对式(15)进行积分求解.通过式(5)和(6)可以分别求得参考高度和参考弹道倾角(实时地面航程Sk+1=Sk+ΔS).当Sk＜SAT时，倾侧角由式(8)求得，否则弹道倾角为零.参考升力系数由式(12)求得，而飞行速度可通过式(14)求得.

3.2 第二段轨迹生成

此段的轨迹计划方法与第一段类似，不同的是将高度能量作为规划的独立变量，以满足飞行器最终的能量要求(即满足飞行器在ALI点的高度和速度要求).因此第二飞行段的欧拉积分公式为

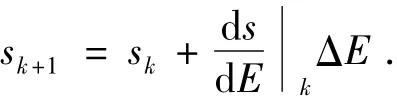
这里的ΔE=(EALI－EHAC)/N.由HAC段的半径公式(4)，在HAC段轨迹生成时剩余航向调整角用以下公式进行更新:

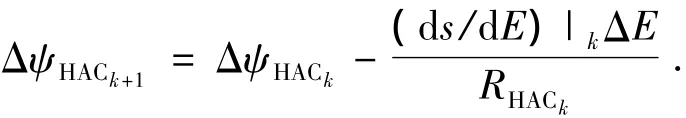
通过规划两段航程最终使终端高度hend满足

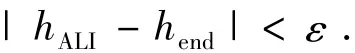
4 制导指令生成

4.1 侧向制导指令生成

参考航天飞机制导指令，倾侧角指令对不同飞行段有不同的形式.捕获段倾侧角指令为

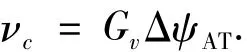
航向调整段倾侧角指令为

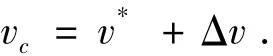
式中v*为由式(9)得到的参考倾侧角指令.而闭环倾侧角指令Δv则由以下形式得到:

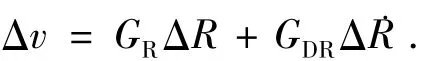
对于预备着陆段倾侧角指令为

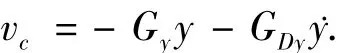
4.2 纵向制导指令生成

纵向法向过载指令nz由开环指令和闭环指令组成，

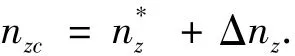
开环的参考过载指令n*z由公式(13)求得.闭环法向过载指令Δnz由以下形式给出:

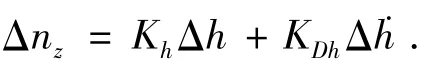
5 仿真分析

取典型的飞行器末端能量管理段参数进行仿真验证，X-33特征面积 S=149.388 m2、质量m=37 362.9 kg，TAEM段开始时刻飞行器高度为28 km，速度为914 m/s，弹道倾角为 －6.7°，航向角为94.6°，X向和Y向位置分别52 450 m、－54 087 m.ALI点的参考高度为3 km，参考速度为158 m/s，弹道倾角 －25°，X向位置 xALI=－8 021 m/s.以 Rf、R2、xNEP、γHAC作为优化变量，对TAEM段轨迹进行优化设计.考虑到升力式飞行器返回特性，给定TAEM段飞行过程中的动压、法向过载、倾侧角和HAC段开始马赫数的约束如下:

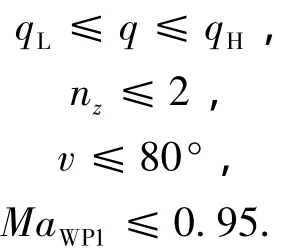
取如下性能指标:

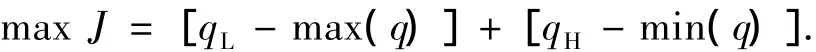
式中 qL=3 800 Pa，qH=20 000 Pa.

本文采用直接打靶法+SQP算法进行优化，得到 Rf=3 657.6 m、R2=262.3 m、xNEP=－9 000 m、γHAC= －18.9°.仿真中，各制导参数设置如下:

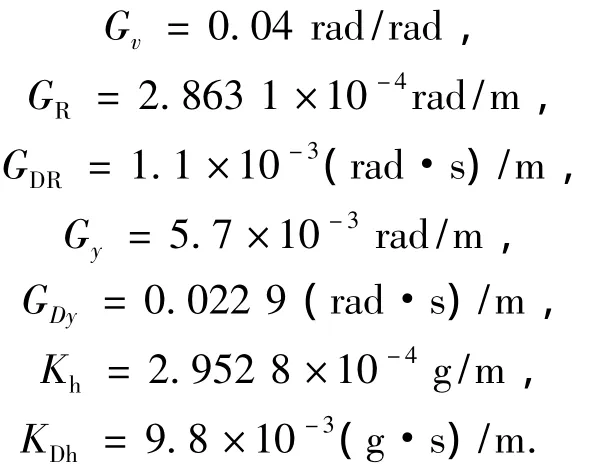
仿真结果如图2～8所示.

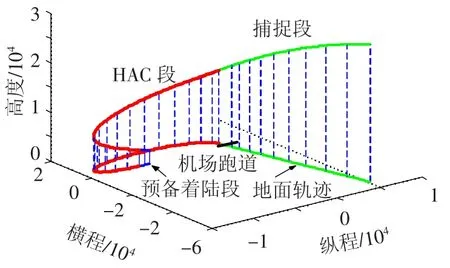
图2 飞行器三维轨迹

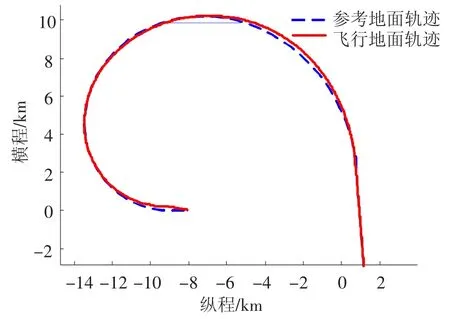
图3 地面轨迹

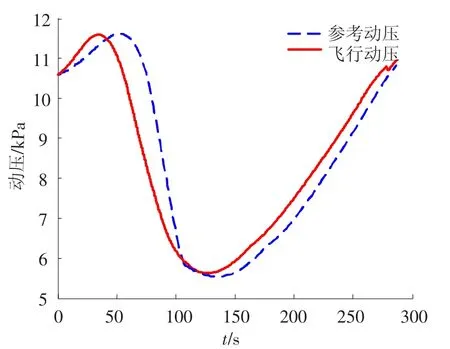
图4 动压变化曲线

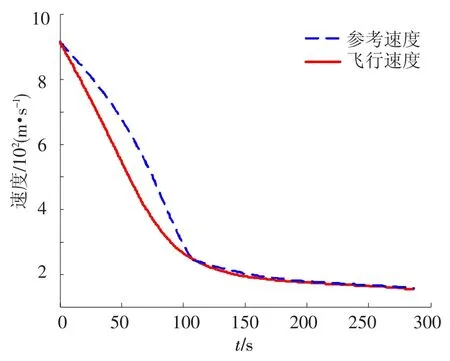
图5 速度变化曲线

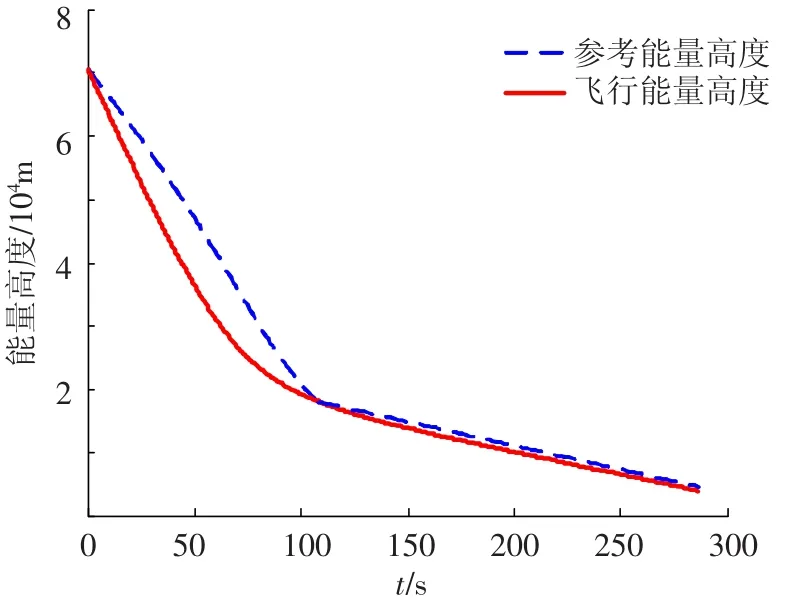
图6 能量高度变化曲线

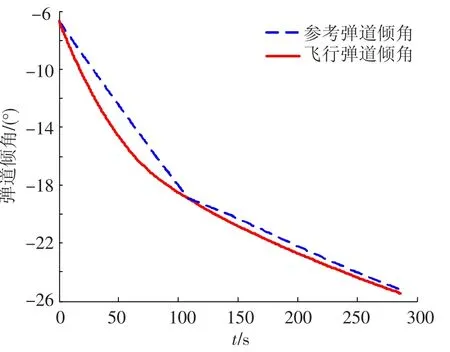
图7 弹道倾角变化曲线

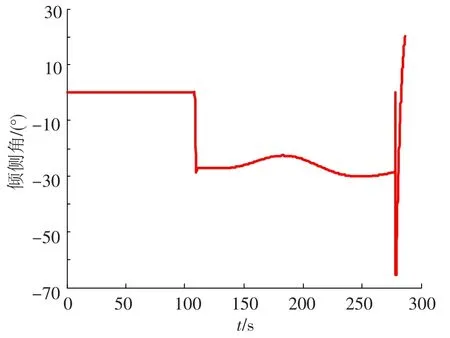
图8 倾侧角变化曲线

以上仿真结果表明，飞行器在预备着陆点(ALI点)的速度偏差为－4.5 m/s，高度方向偏差为－234.5 m，X和Y方向的位置偏差分别为50 m和30 m.通过优化设计的TAEM段轨迹，满足要求的各项约束要求，制导方法也具有良好的制导精度.

6 结论

以第二代升力式再入飞行器为应用背景，对飞行器再入飞行后的末端能量管理方法进行了深入的研究和分析.在参考航天飞机TAEM段能量管理方法的基础上，进行TAEM段轨迹组成分析，优化设计了飞行器TAEM段轨迹，并进行了纵向和侧向制导律设计.仿真结果表明本文优化设计的TAEM段轨迹满足升力式再入飞行器的末端能量管理段飞行约束条件，制导方法具有较高的精度和适应性，能够满足第二代升力式再入飞行器末端能量管理要求.

［1］赵汉元.飞行器再入动力学与制导［M］.长沙:国防科技大学出版社，1997:16.

［2］沃云峰.可重复使用飞行器末端能量管理段轨迹与制导［D］.西安:西北工业大学，2005:13－44.

［3］MOORE T E.Space shuttle entry terminal area energy management［R］.NASA Lyndon B:Johnson Space Center，1991:1 －30.

［4］KLUEVER C A.Rapid terminal-trajectory planner for an unpowered reuseable launch vehicle［C］//AIAA Guidance，Navigation，and Control Conference.Chicago，Illinois，2009，AIAA 2009－5766:1－13.

［5］KLUEVER C A.Terminal guidance for an unpowered reusable launch vehicle with bank constraints［J］.Journal of Guidance，Control and Dynamics，2007，30(1):1 －15.

［6］SCHIERMAN J D，HULL J R，WARD D G.Adaptive guidance with trajectory reshaping for reusable launch vehicles［C］//AIAA Guidance，Navigation，and Control Conference and Exhibit.Chicago:AIAA，2002:1 －9.

［7］HORNEMAN K R，KLUEVER C A.Terminal area energy management trajectory plannning for an unpowered reusable launch vehicle［C］//AIAA Atmospheric Flight Mechanics ConferenceandExhibit.RhodeIsland:［sn.］，2004，AIAA 2004－5183:1－18.

［8］LU P.Predictor-corrector entry guidance for low-lifting vehicles［J］.Journal of Guidance，Control，and Dynamics，2008，31(4):1067 －1075.

［9］LU P，XUE S.Rapid generation of accurate entry landing footprints［J］.Journal of Guidance，Control，and Dynamics，2010m 33(3):756 －767.

［10］De RIDDER S，MOOIJ E.Optimal terminal-area strategies and energy-tube concept for a winged re-entry vehicle［C］//AIAA Guidance，Navigation，and Control Conference and Exhibit 2009.Chicago:AIAA，2009:1688－1708.

The method of terminal area energy management for lifting reentry vehicle

CHEN Gong1，2，XIE Zhi-jun2，CUI Nai-gang1

(1.Dept.of Space Engineering，Harbin Institute of Technology，150001 Harbin，China;2.State Key Laboratory of Aerodynamics，621000 Mianyang，China)

According to the application of the 2ndgeneration lifting reentry vehicle，a further research and analysis was performed for the TAEM.Based on the space shuttle＇s trajectory and guidance of TAEM，several parameters of TAEM trajectory are analyzed，and the ground trajectory and altitude profiles of TAEM are designed by optimization.Also，the longitudinal and lateral guidance laws are given in order to make simulation verification for the reference trajectory.Simulation results satisfy all of the trajectory constraints，and the guidance algorithm has been proved effective and accurate.The guidance method validates that the guidance is feasibility and validity for TAEM of the 2nd generation lifting reentry vehicle.

terminal area energy management;reentry vehicle;trajectory optimization

V448.2

A

0367－6234(2012)09－0020－05

2011－05－03.

陈 功(1985—)，男，助理工程师;

崔乃刚(1964—)，男，教授，博士生导师.

陈 功，success850012@163.com.

(编辑 张 宏)