分组对称旋转周期结构固有频率分裂解析分析

王世宇 ，陈东亮，刘建平，宋轶民，曹树谦 ，张 策

(1. 天津大学机械工程学院，天津 300072；2. 天津市非线性动力学与混沌控制重点实验室，天津 300072)

为了改善动力学特性，许多传动/动力系统都尽量采用对称构型，如齿轮、电机定/转子和振动陀螺仪等．该类结构可视为由若干相同构型的对称单元通过圆周阵列组合而成．对称单元的分布显著影响结构的动力学特性，例如固有频率分裂现象．在齿轮和电机领域，固有频率分裂将导致复杂的动力学行为，严重影响系统的稳定性[1]；在超声电机领域，固有频率分裂将产生行波畸变，严重影响了运行效率和稳定性[2]；在振动陀螺仪领域，必须将固有频率分裂程度限制在0.01%以内，否则将产生巨大危害[3]．

为了阐明旋转周期结构的拓扑结构对动力学特性的影响，国内外学者开展了大量的研究工作，甚至可以追溯到早期对教堂钟的声学研究[4]．在分析方法上，文献[1]提出了有限元法，文献[5-6]提出了一种近似方法．其中，文献[5]将行星传动的内齿圈视为光滑圆环，采用有限元法研究了其模态特性．文献[6]采用阻抗矩阵研究了环形超声定子的振动特性．显然，有限元方法通常计算规模较大，而近似方法得到的结果通常不够精确，尤其是难以反映对称单元对动力学特性的影响[4,7-8]．

为了准确揭示对称单元对动力学特性的影响规律，国内外学者针对常见环形和盘形周期结构开展了深入研究．对于环形结构，主要研究了其面内振动，并充分考虑了附加点质量[9-10]、任意截面轮廓[11]和支撑刚度[8]的影响．其中，Fox等[9-10]研究了固有频率分裂的抑制问题，还采用傅里叶级数和 Rayleigh-Ritz方法研究了任意截面轮廓薄圆环的面内振动，最终揭示了固有频率分裂与圆环轮廓线所含谐波成分之间的关系[11]；Parker等[8]采用傅里叶级数、摄动法和伽辽金方法研究了弹性支撑薄圆环的面内振动，得到了固有频率的分裂规则．为了提高计算精度，还应用二阶摄动方法进行分析，得到了与一阶摄动结果相同的固有频率分裂规则．

对于盘形周期结构，现有文献考虑了径向槽[1]、任意截面轮廓[12]、轴向支撑[13]和附加扇形单元[7]的影响．其中，Mote等[1]采用摄动方法研究了径向槽对薄圆盘固有频率分裂的影响；Parker等[12]分析了准圆形薄板的自由振动，证明了不规则截面轮廓将导致固有频率分裂；Wickert等[13]分析了均布轴向支撑的盘形薄板的振动，揭示了固有频率分裂与附加支承刚度之间的关系，还研究了均布扇形单元的周期结构的振动特性，并指出固有频率的分裂与2nN(n为波数，N为单元数)是否为整数密切相关[7]．

应当指出，上述研究均针对对称单元均布的旋转周期结构．事实上，在工程实际中，还大量应用非均布对称单元，例如采用非均布行星轮以改善动力学特性[14]，采用非均布齿槽/磁极以减小转矩脉动和不平衡磁拉力[15-21]，采用非均布压电陶瓷以获得纯行波[22-23]．近年来，文献[9]研究了均布/径向对称弹簧支撑的旋转周期结构的自由振动，并指出非均布构型将显著改变结构的动力学特性．对于其他分组方式对旋转周期结构动力学性能的研究，还鲜有文献提及．

综上所述，笔者拟以环状旋转周期结构为典型，采用摄动法研究对称单元的拓扑结构对固有频率分裂的影响，揭示二者之间的映射关系，并初步探讨该映射关系在抑制固有频率分裂方面的应用．

1 旋转周期结构数学建模

1.1 对称模式及等效对称单元

图1为工程领域常见的各类旋转周期结构，该周期结构的对称模式可以归结为均布模式和分组模式2类．前者的对称单元沿周向均匀分布，如图 1(a)～(d)所示，而后者具有分组布置的对称单元，如图1(e)～(h)所示．

为了研究分组对称旋转周期结构的动态特性，可将每个分组视为等效单元．如果将图 1(f)所示任意相邻的2个单元视为一个等价分组，则整体上可等效为均布的 4个对称单元．事实上，该方法将分组模式等效为均布模式，因而可利用均布旋转周期结构的现有结论初步预测固有频率的变化规律．

图1 旋转周期结构Fig.1 Configurations of rotationally periodic structure

1.2 数学模型

采用具有附加对称单元的二维弹性薄圆环模拟旋转周期结构，仅考虑其无延展弯曲振动．图 2为该结构的计算模型．坐标系{O,r,θ}的原点与周期结构的几何形心重合，极轴穿过第1组的第1个对称单元的中心．u(θ,t)和v(θ,t)分别为切向和径向位移．m、EI和 r0分别为标准圆环的线密度、弯曲刚度和半径．mt和kt分别表示对称单元的质量和刚度．N1为单元分组数，第i组记为 Gi( i = 1 ,2,… ,N1)，每组含 N2个单元．Dji( i = 1,2,… ,N1， j = 1 ,2,… ,N2)表示第i组第j个单元．ψi(i = 1 ,2,… ,N1)为第i组的位置角．αik(i = 1,2,… ,N1，k = 1 ,2,… ,N2)为第i组第k个单元的位置角．不失一般性，令ψ1=0，α11=0．事实上，该模型可视为具有 N1个均布等效对称单元的旋转周期结构．

图2 含分组对称单元的旋转周期结构Fig.2 Configuration of rotationally periodic structure with grouped features

2 固有频率分析

2.1 摄动法求解

标准圆环的振动方程[24]为

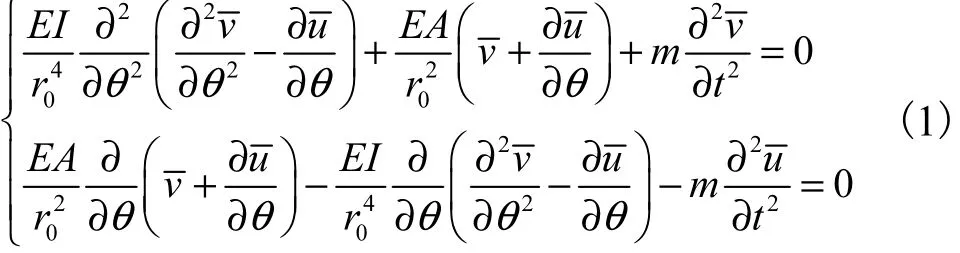
式中A为圆环的截面积．

仅考虑无延展振动，因此u(θ,t)和v(θ,t)满足

由式(1)和式(2)可得

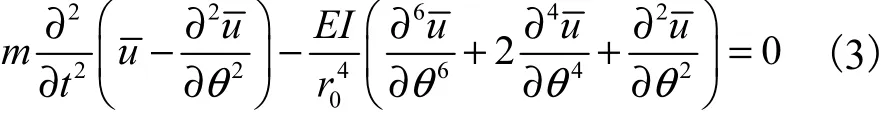
假设u = u /r0，t = t /T(T =，将其代入式(3)得

式中 M(0)和K(0)分别为质量及刚度算子，且

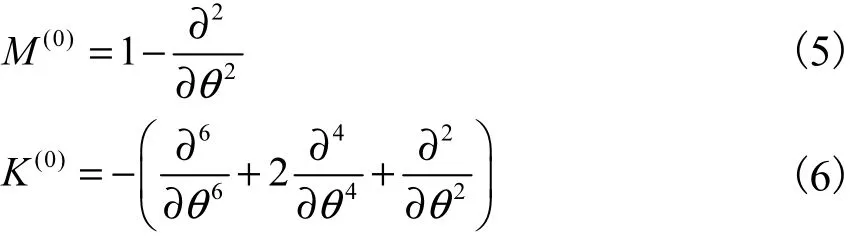
旋转周期结构的动力学方程可表示为

其中

式中ε为无量纲小参数．显然，与ε=0对应的系统为标准圆环，而 ε M(1)和εK(1)分别为线质量密度和刚度的变化，M(1)和K(1)分别为质量和刚度的摄动．

假设 u ( θ ,t ) = u ( θ)ejωt，将其代入式(7)可得特征方程

式中λ (λ =ω2)为结构的特征值．

根据摄动法，式(10)的解可以表示为小量ε的级数展开

式中n为波数．

将式(8)、式(9)、式(11)和式(12)代入式(10)，且令ε 的各阶系数为零，可得递归方程

定义内积

式中符号*表示共轭．

假设

根据正则化条件

根据正则化条件，式(21)左端应为零，即

由式(22)可得

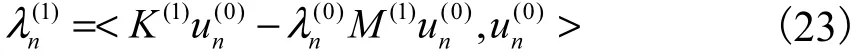
2.2 固有频率分析

采用点质量和点刚度来描述旋转周期结构的对称单元，则算子 M(1)和K(1)可分别表示为

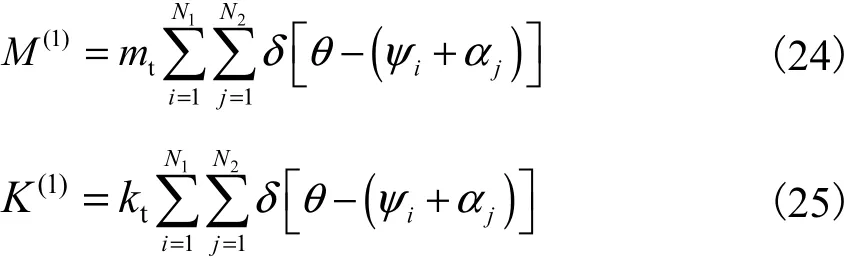
式中：mt(mt= mt/m)和kt(kt= kt/ E I)分别为无量纲质量和刚度；ψi(ψi=2π(i - 1 )/N1，i = 1 ,2,… ,N1)为第i组对称单元的位置角，αj(αj=(j-1)α，α为组内相邻单元之间的夹角，j = 1 ,2,… ,N2)为组内第j个单元的位置角．

将式(24)和式(25)代入式(23)，整理可得

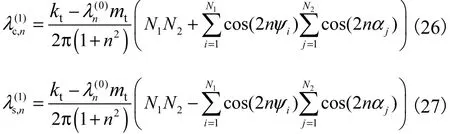
根据三角函数的运算特性，有

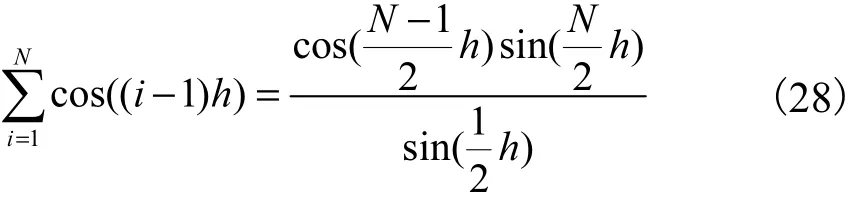
式中N为正整数．

因此，式(26)和式(27)可分别改写为

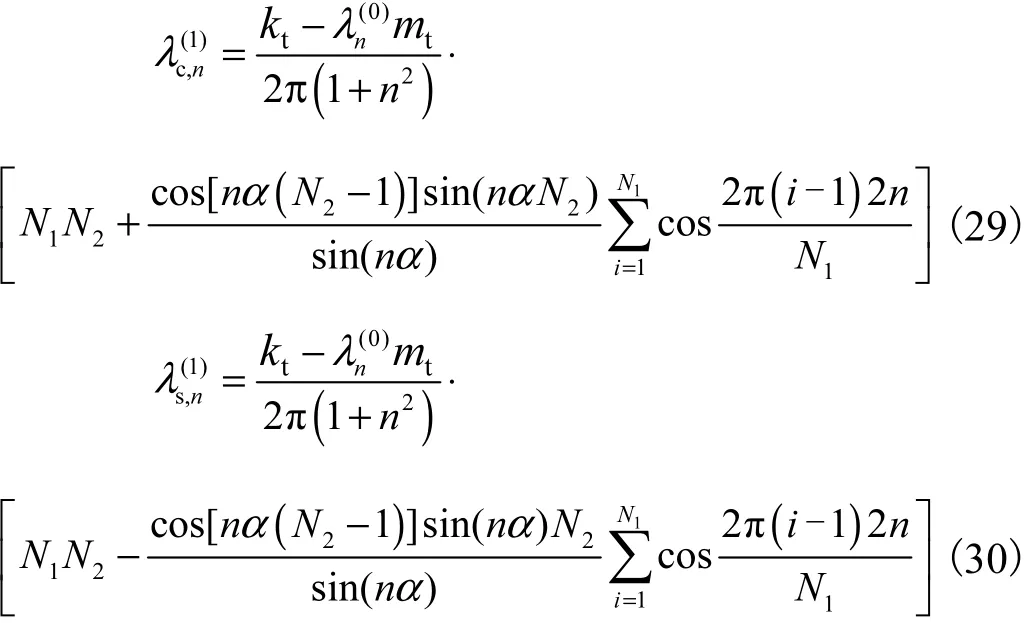
由式(29)和式(30)可得表 1所述结论(其中q和q′均为正整数)．

表1 分组旋转周期结构固有频率分裂规律Tab.1 Natural frequency splitting behavior of rotationally periodic structure with grouped features

若采用等效对称单元假设，该分组旋转周期结构可视为具有 N1个对称单元的均布旋转周期结构．根据表 1，若 2 nN1不为整数，则相应固有频率必然重合，并且该结论与组内对称单元的分布无关．该条件可用于初步判断是否产生固有频率分裂．对于 2 nN1为整数的情形，固有频率分裂与否还取决于组内对称单元的具体分布．

3 仿真验证

3.1 基本参数

鉴于固有频率分裂对超声电机性能的显著影响，以筒形超声定子为例验证表 1所述固有频率变化规律．不失一般性，取对称单元为压电陶瓷．表 2给出了图 2所示的超声定子的物理及部分几何参数；其中，r1＝0.019,m，r2＝0.018,m，r3＝0.021,m，β＝π/15．

表2 超声定子基本参数Tab.2 Parameters of the ultrasonic stator

3.2 理论分析

依据表 1可预测周期结构的固有频率的变化规律．假定{N1,N2,α} ＝{2,2,π/6}、{3,2,π/6}、{2,3,π/6} 、{4,2,π/6} 、{4,2,π/8} 、{6,2,π/12}、{2,6,π/12}、{4,3,π/12}和{3,4,π/12}，对于{4,2,π/6}，由于存在 4个等效对称单元，若 n = 3 ,5,7…，则固有频率重合．显然，该判别方法仅涉及 N1．对于{4,2,π/8}和{4,3,π/12}可以得到相同的结论．同理，对于{6,2,π/12} 、{3,2,π/6} 和 {3,4,π/12} ，若 n=2,4,5,7，…，固有频率仍然重合．对于固有频率分裂的情况，还需进一步考察参数 N2和α是否满足表 1所述的匹配关系，才能准确判断频率分裂规律．对于{4,2,π/6}和{4,3,π/12}，当n＝2 或4时频率分裂与否由组合{α , n ,N2}确定．以{4,2,π/6,4}为例，因为夹角α=π6不满足频率重合条件：α=(2 q − 1)π /[2n⋅(N2-1)]) = ( 2q −1)/8(α ≠q′ π /n = q′π/4)和 α=qπ/(n N2) = q π/8(α ≠q′ π /n = q′π/4)，所以相应固有频率将产生分裂现象．同理，与{4,2,π/6,2}、{4,2,π/8,2}、{4,3,π/12,2}和{6,2,π/12,3}对应的固有频率也将分裂．但对于{4,3,π/12,4}，因为 α = π /12满足频率重合条 件 α =q π (n N2) = qπ/12(α ≠q′ π /n =q′π/4)，因此相应固有频率不分裂．同理，与{4,2,π/8,4}、{6,2,π/12,6}、{3,4,π/12,3}和{3,4,π/12,6}对应的固有频率也为重根．以上结果表明，若 2 n≠qN1，则固有频率必然重合，且与组内单元的具体分布无关；若2n = q N1，则固有频率是否分裂还与 N2、α与n的具体组合有关．

3.3 仿真计算

根据表 2所述基本参数建立超声定子的二维有限元模型，并计算定子的模态．在仿真计算中，单元类型为 PLANE2，单元尺寸为 0.000,15,m．具体计算结果如表3和图3所示．以参数组合{N1,N2,α,n,}＝{4,2,π/6,4}和{4,2,π/8,4}为例，在不改变 { N1,N2}的前提下将α由π/6调整为π8，若忽略计算误差，原分裂固有频率(8,764,Hz，9,356,Hz)变为重频(9,031,Hz，9,040,Hz)．在不改变单元总数的前提下，改变分组方式也可抑制频率分裂．观察{2,3,π/6,3}和{3,2,π/6,3}可知，将原分组方案 { N1, N2}＝{2,3}变为{3,2}，原分裂固有频率(4,762,Hz，4,932,Hz)变为重频(4,824,Hz，4,827,Hz)．不改变分组数 N1，通过调整组内单元数 N2和夹角α也可抑频率分裂．比较参数组合{4,2,π/6,4}和{4,3,π/12,4}可以发现，在不改变分组数 N1的情况下，将组内单元参数{N2,α}由{2,π/6} 调整为{3,π/12}，则原分裂频率(8,764,Hz，9,356,Hz)变为重频(8,742,Hz，8,746,Hz)．在保证组内单元数目2N和夹角α不变的前提下，可增加或减少组数，也可使固有频率重合，如参数组合{4,2,π/6,2}和{3,2,π/6,2}所述，分裂固有频率(1,640,Hz，1,716,Hz)变为重频(1,708,Hz，1,709,Hz)．

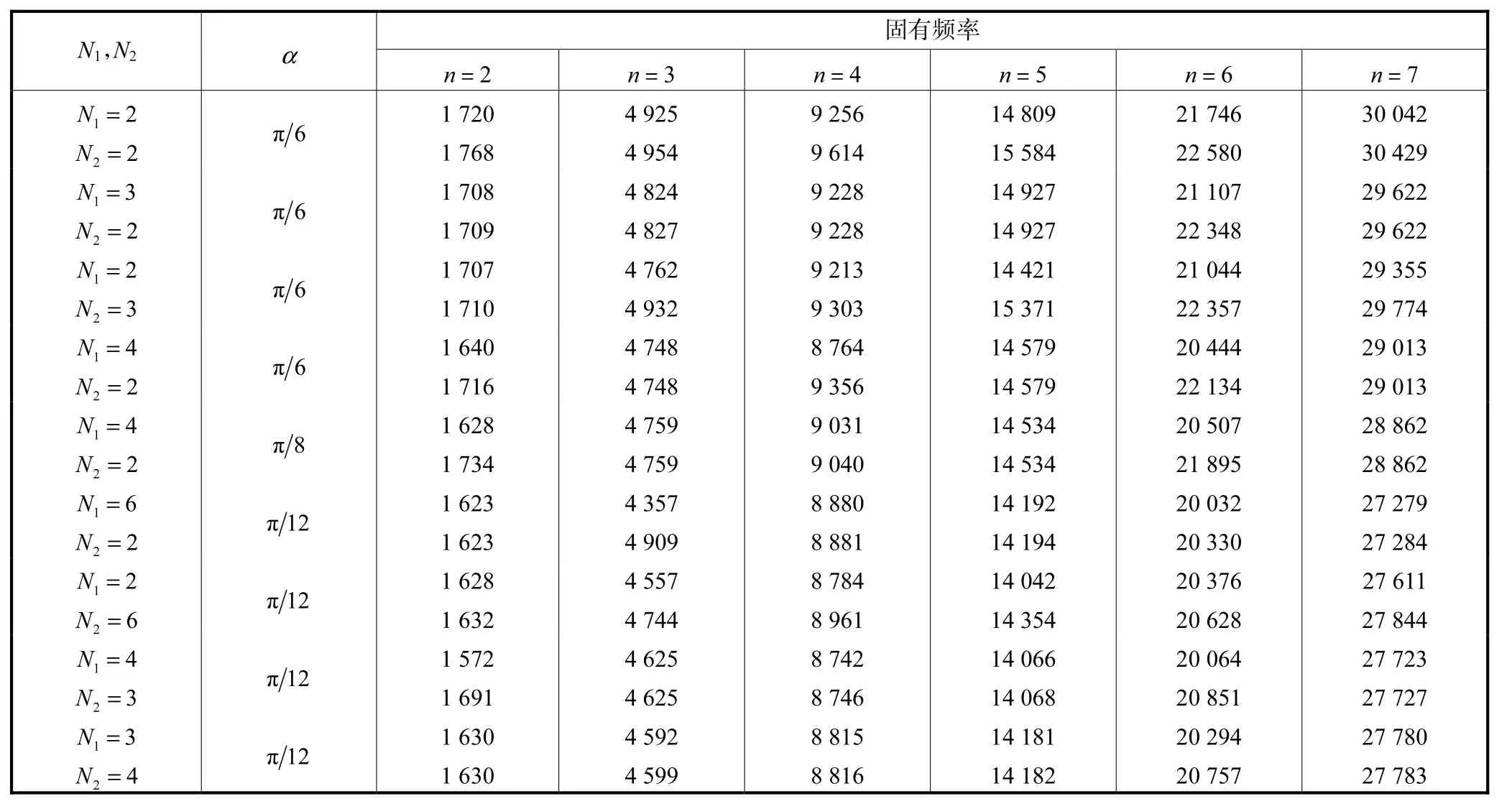
表3 超声定子固有频率Tab.3 Natural frequencies of the ultrasonic stator Hz

图3 超声定子振型Fig.3 Mode shapes of ultrasonic stator

4 结 语

本文研究了环状旋转周期结构的面内无延展振动，揭示了拓扑结构对固有频率分裂的影响规律，提出一种可判断固有频率是否分裂的等效对称单元法．若波数n和分组数N1满足 2 n≠qN1，即使改变组内单元数及单元之间的夹角，固有频率仍然重合；若满足 2 n = q N1，则固有频率可能分裂．对于频率分裂情形，可调整分组数、组内单元数及单元之间的夹角对其进行抑制．该研究在超声电机和振动陀螺仪等对固有频率分裂敏感的重要领域具有应用价值．有限元仿真结果证明了理论分析的正确性．

［1］ Yu R C，Mote C D. Vibration and parametric excitation in asymmetric circular plates under moving loads[J].Journal of Sound and Vibration，1987，119(3)：409-427.

［2］ 赵淳生. 超声电机技术与应用[M]. 北京：科学出版社，2007.Zhao Chunsheng. Ultrasonic Motors Technologies and Applications[M]. Beijing：Science Press，2007(in Chinese).

［3］ Rourke A K，McWilliam S，Fox C H J. Multi-mode trimming of imperfect thin rings using masses at preselected locations[J]. Journal of Sound and Vibration，2002，256(2)：319-345.

［4］ Kim M，Moon J，Wickert J A. Spatial modulation of repeated vibration modes in rotationally periodic structures[J]. Journal of Vibration and Acoustics，Transactions of the ASME，2000，122(1)：62-68.

［5］ Tanna R P，Lim T C. Modal frequency deviations in estimating ring gear modes using smooth ring solutions[J]. Journal of Sound and Vibration，2004，269(3/4/5)：1099-1110.

［6］ Kim Y H，Ha S K. Analysis of a disk-type stator for the piezoelectric ultrasonic motor using impedance matrix[J]. Journal of Sound and Vibration，2003，263(3)：643-663.

［7］ Chang J Y，Wickert J A. Response of modulated doublet modes to traveling wave excitation[J]. Journal of Sound and Vibration，2000，242(1)：69-83.

［8］ Wu X，Parker R G. Vibration of rings on a general elastic foundation[J]. Journal of Sound and Vibration，2006，295(1/2)：194-213.

［9］ Fox C H J. A simple theory for the analysis and correction of frequency splitting in slightly imperfect rings[J].Journal of Sound and Vibration，1990，142(2)：227-243.

［10］ Rourke A K，McWilliam S，Fox C H J. Multi-mode trimming of imperfect thin rings using masses at preselected locations[J]. Journal of Sound and Vibration，2002，256(2)：319-345.

［11］ Fox C H J，Hwang R S. McWilliam S. The in-plane vibration of thin rings with in-plane profile variations(part II)：Application to nominally circular rings[J]. Journal of Sound and Vibration，1999，220(3)：517-539.

［12］ Parker R G，Mote C D. Exact perturbation for the vibration of almost annular or circular plates[J]. Journal of Vibration and Acoustics，1996，118(3)：436-445.

［13］ Tseng J G，Wickert J A. On the vibration of bolted plate and flange assemblies[J]. ASME Journal and Acoustics，1994，116(4)：469-473.

［14］ Lin J，Parker R G. Structured vibration characteristics of planetary gears with unequally spaced planets[J]. Journal of Sound and Vibration，2000，233(5)：921-928.

［15］ Lundström N L P，Aidanpää J-O. Dynamic conesquences of electromagnetic pull due to deviations in generator shape[J]. Journal of Sound and Vibration，2007，301(1/2)：207-225.

［16］ Colby R S，Mottier F M，Miller T J E. Vibration modes and acoustic noise in a four-phase switched reluctance motor[J]. IEEE Transactions on Industry Applications，1996，32(6)：1357-1364.

［17］ Ishikawa T，Inaba H，Matsunami M. Comparison of vibration characteristics of several interior permanent magnet synchronous motors[C]// International Conference on Electrical Machines and Systems，ICEMS 2008.Wuhan，China，2008：314-319.

［18］ Centner M，Hanitsch R. Fractional slot-winding with asymmetrical stator-slot layout[C]//SPEEDAM 2006，International Symposium on Power Electronics，Electrical Drives，Automation and Motion. Taormina，Italy，2006：108-110.

［19］ Bretón C，Bartolomé J，Benito J A，et al. Influence of machine symmetry on reduction of cogging torque in permanent-magnet brushless motors[J]. IEEE Transactions on Magnetics，2000，36(5)：3819-3823.

［20］ 王秀和. 永磁电机[M]. 北京：中国电力出版社，2007.Wang Xiuhe. Permanent Magnetic Motor[M]. Beijing：China Electric Power Press，2007(in Chinese).

［21］ Stirban A，Tutelea L，Iles-Klumpner D，et al. FEM analysis of concentrated coils nonuniform slot(6+6/8)IPMSM fed with trapezoidal current[C]// 11,th International Conference on Optimization of Electrical and Electronic Equipment，2008，OPTIM. Timisoara，Romania，2008：45-53.

［22］ 董云朝，刘景全，杨志刚，等. 圆筒压电振子产生周向行波的激励原理[J]. 压电与声光，2002，24(1)：64-67.Dong Yunzhao，Liu Jingquan，Yang Zhigang，et al.Traveling-wave excitation principle of cylindrical vibrator in circumferential direction[J]. Piezoelectrics and Acoustooptics，2002，24(1)：64-67(in Chinese).

［23］ Isobe H，Kyusojin A. Frequency characteristics of noncontact ultrasonic motor with motion error correction[J].Precision Engineering，2007，31(4)：351-357.

［24］ 贾启芬，刘习军. 机械与结构振动[M]. 天津：天津大学出版社，2007.Jia Qifen，Liu Xijun. Mechanical and Structural Vibration [M]. Tianjin：Tianjin University Press，2007(in Chinese).