利用数码相机进行摄影测量的精度研究

陈海玉， 秦 丽，李文君

(湖北文理学院 建筑工程学院，湖北 襄阳 441053)

摄影测量技术在航空、探矿、医学、工业、建筑等领域中的应用已有较长的历史，由于摄影测量过程中无需接触目标物，因而所获信息内容丰富、数据客观，并且可以在人员无法接近的环境中完成测量工作[1.2.3].随着数码相机的普及，更多普通工作者试图采用普通数码相机进行测量工作，但数据的精度一向受人质疑. 经分析，测量过程中，数据误差产生的原因可能有：1)普通数码相机不能精确定位；2)镜头有畸变；3)待测试件表面反光使得图片局部模糊；4)光线折射引起误差[1]；5)拍照时相机位置有轻微变动. 这些影响因素中，试件表面反光可以通过加强重点观测部位的色差、改变拍摄角度、避开反光加以避免；相机不能精确定位及拍照时相机位置轻微变动可以通过给每幅照片都建立单独的物-像投影关系予以解决，工作量虽然稍大些，但准确度更高，且借助软件技术，人员工作量并无大量增加. 接下来重点讨论镜头畸变误差和光学折射误差的产生原因和计算方法.

1 误差计算方法

相机系统由于设计、制作和装配所引起的像点偏离其立项位置的点位误差称之为光学畸变差，简言之，若拍摄实物为一条直线，而相片中却极可能是一条曲线.

图1 光学畸变

设物方摄入光线与摄影机物镜光轴的夹角为a(见图1)，而其构象点离像片主点o的辐射距离为r，则当r=ftana时，则该物镜无畸变差，f为摄影机主距. 严格上说，制造无畸变差的物镜是不可能. 设实际构象的辐射距为r，则其差值为：

即为畸变差. 由该式可知物镜畸变差值与所选用的摄影机常数f有关. 但由于制作工艺问题，f通常也是有误差的，这样一来，镜头畸变不仅包含关于主点对称的径向畸变，还包含不对称的非径向畸变. 参考文献[4]中提出畸变误差的计算式为：

式中，x、y为像点直角坐标值，R为像点到相片主点辐射距，K1、K2、K3为畸变系数. 此式中，xy项考虑了非径向畸变，其它项用以计算径向畸变，而K1、K2、K3三个畸变系数可有任意2个或2个以上控制点的已知坐标求出.

光线从待测点位置发射出来，投射到物镜系统，要经过空气，由于待测点距物镜距离较近，空气密度可视为不变，可以不考虑空气对光线的折射影响，但若是隔着玻璃观测试件，玻璃引起的折射不能忽略. 假设玻璃厚度为d，镜头与玻璃的距离为l，光线入射角为a，折射角为b，已知玻璃折射率为n，可以用下面的公式来求出玻璃后点坐标的折射改正值.

如图所示：

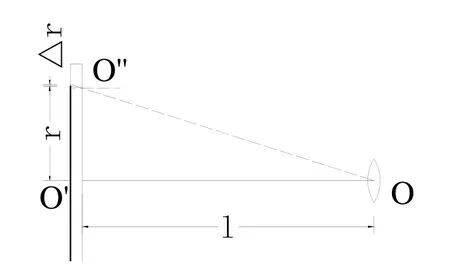
图2 光的折射

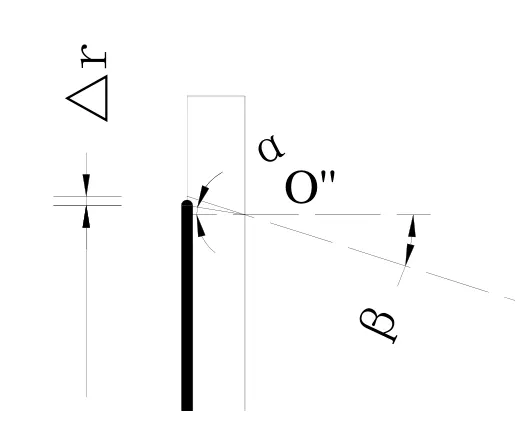
图3 放大图

所以

2 误差试验研究

在平滑的墙面上设计如下网格点阵:网格点正交，布局为 7×7，间距 40mm(如图 4)，以中心点 0为原点，建立坐标系，可得到每点的物方坐标值；用数码相机拍下像片，对像片进行量测，获得点的像方坐标值.

1)选取3-5个点待测平面控制点，根据其物、像坐标值建立初始平面投影关系.

2)利用平面投影关系推算其它点的物坐标，从而计算出与实测值的坐标差值ixD，iyD，代入式(2)中求出镜头畸变系数.

3)利用畸变差计算公式反推控制点坐标的修正值，再重新建立平面投影管. 反复计算，直至收敛.

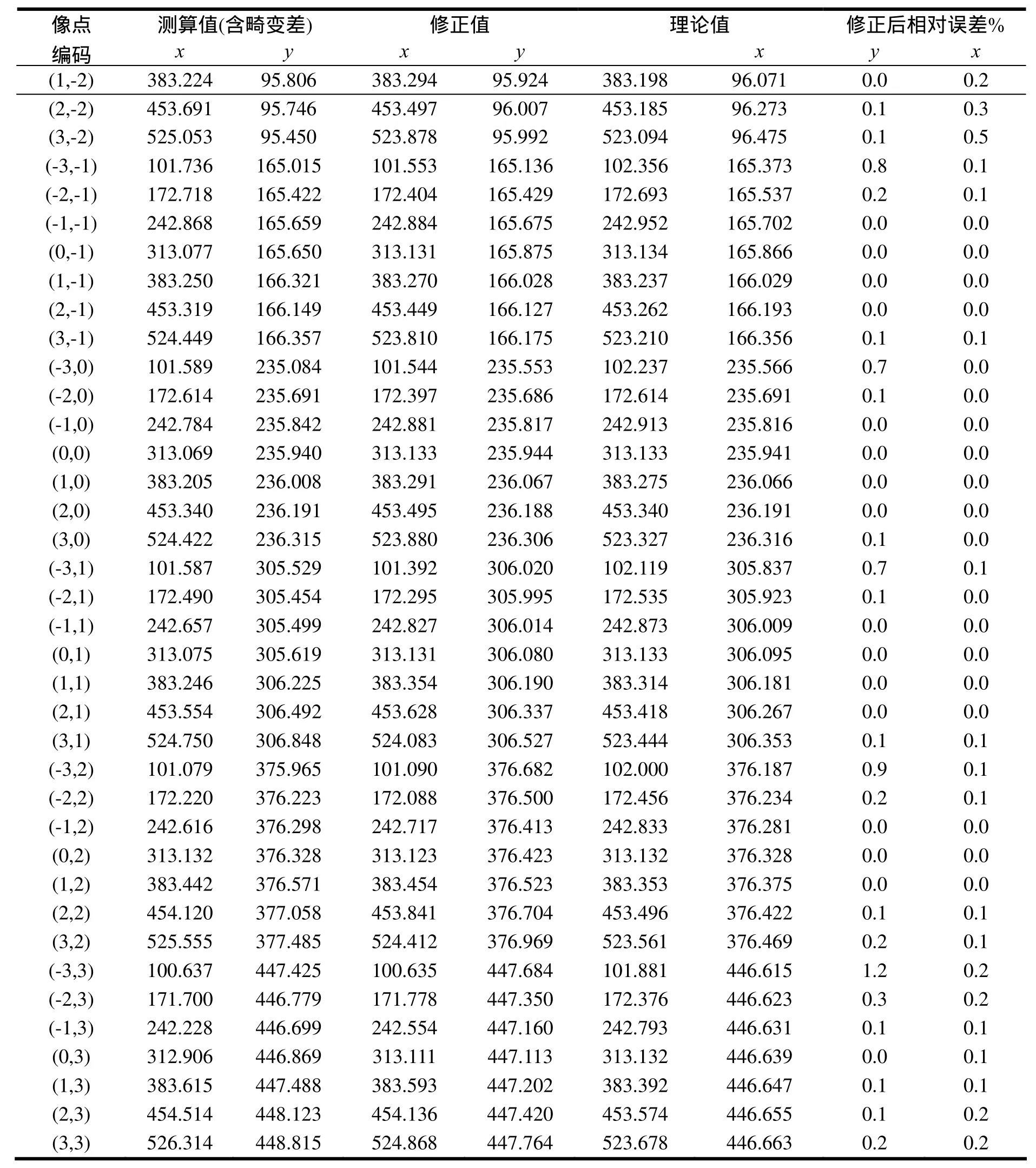
表1列出了各点像坐标理论值(因实物为间距相等的正交点阵，则如无误差，相片上的点也应为正交点阵，据此推算像点坐标，称为理论值)、测算值(利用图片处理程序直接提取像点坐标，含有畸变差)和测算修正值，对比如下：

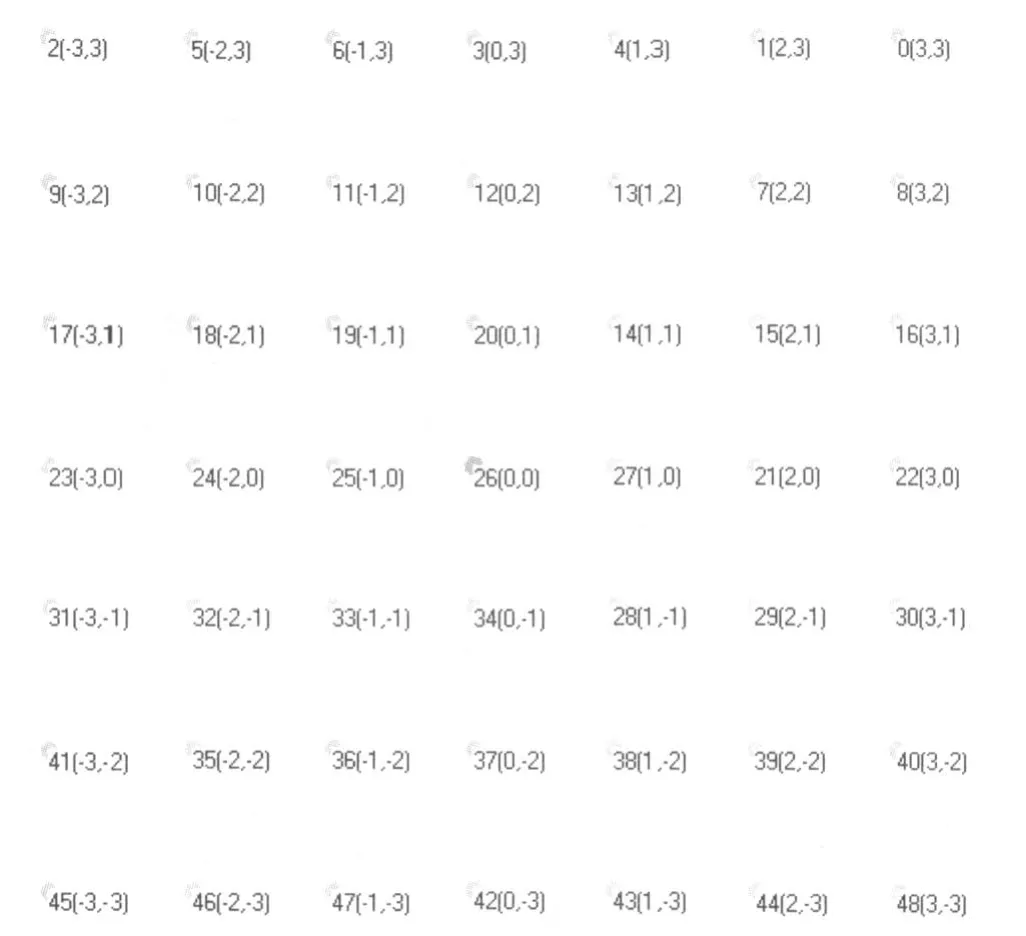
图4 7×7正交点阵

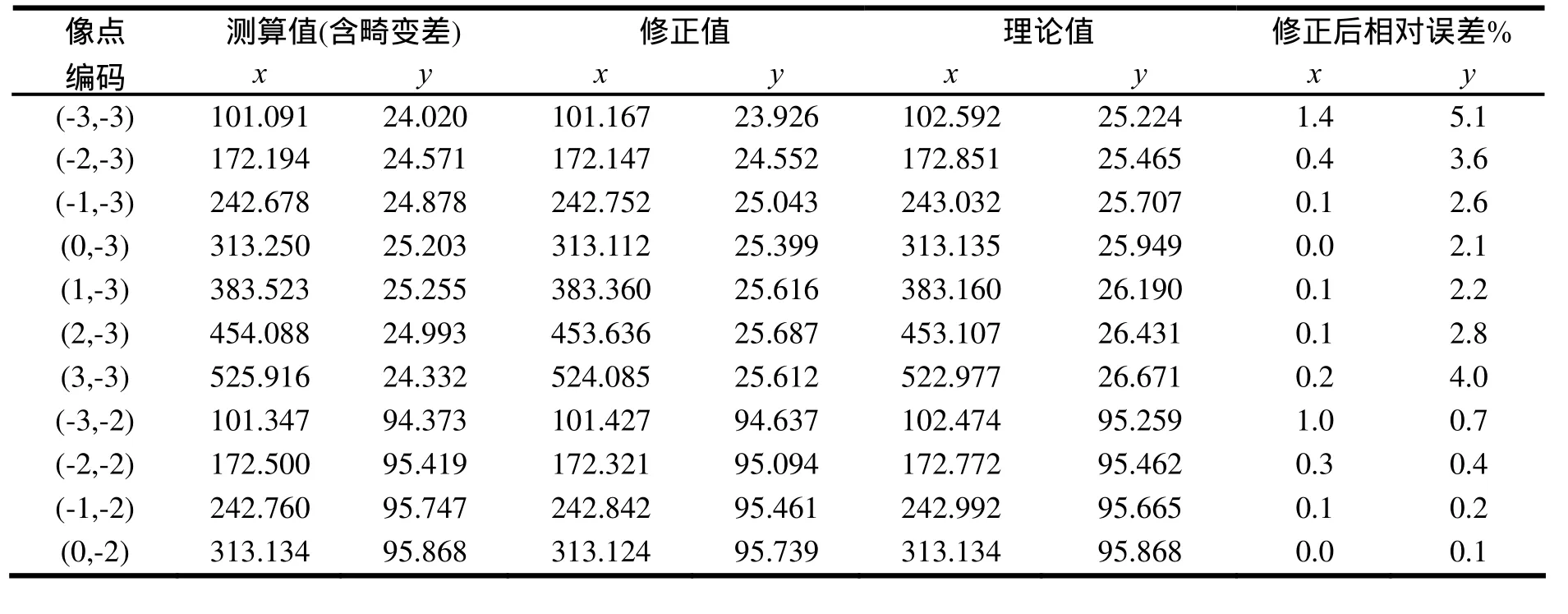
表1 三参数模型与五参数模型坐标修正值表

测算值(含畸变差) 修正值 理论值 修正后相对误差%像点编码 x y x y x y x(1,-2) 383.224 95.806 383.294 95.924 383.198 96.071 0.0 0.2(2,-2) 453.691 95.746 453.497 96.007 453.185 96.273 0.1 0.3(3,-2) 525.053 95.450 523.878 95.992 523.094 96.475 0.1 0.5(-3,-1) 101.736 165.015 101.553 165.136 102.356 165.373 0.8 0.1(-2,-1) 172.718 165.422 172.404 165.429 172.693 165.537 0.2 0.1(-1,-1) 242.868 165.659 242.884 165.675 242.952 165.702 0.0 0.0(0,-1) 313.077 165.650 313.131 165.875 313.134 165.866 0.0 0.0(1,-1) 383.250 166.321 383.270 166.028 383.237 166.029 0.0 0.0(2,-1) 453.319 166.149 453.449 166.127 453.262 166.193 0.0 0.0(3,-1) 524.449 166.357 523.810 166.175 523.210 166.356 0.1 0.1(-3,0) 101.589 235.084 101.544 235.553 102.237 235.566 0.7 0.0(-2,0) 172.614 235.691 172.397 235.686 172.614 235.691 0.1 0.0(-1,0) 242.784 235.842 242.881 235.817 242.913 235.816 0.0 0.0(0,0) 313.069 235.940 313.133 235.944 313.133 235.941 0.0 0.0(1,0) 383.205 236.008 383.291 236.067 383.275 236.066 0.0 0.0(2,0) 453.340 236.191 453.495 236.188 453.340 236.191 0.0 0.0(3,0) 524.422 236.315 523.880 236.306 523.327 236.316 0.1 0.0(-3,1) 101.587 305.529 101.392 306.020 102.119 305.837 0.7 0.1(-2,1) 172.490 305.454 172.295 305.995 172.535 305.923 0.1 0.0(-1,1) 242.657 305.499 242.827 306.014 242.873 306.009 0.0 0.0(0,1) 313.075 305.619 313.131 306.080 313.133 306.095 0.0 0.0(1,1) 383.246 306.225 383.354 306.190 383.314 306.181 0.0 0.0(2,1) 453.554 306.492 453.628 306.337 453.418 306.267 0.0 0.0(3,1) 524.750 306.848 524.083 306.527 523.444 306.353 0.1 0.1(-3,2) 101.079 375.965 101.090 376.682 102.000 376.187 0.9 0.1(-2,2) 172.220 376.223 172.088 376.500 172.456 376.234 0.2 0.1(-1,2) 242.616 376.298 242.717 376.413 242.833 376.281 0.0 0.0(0,2) 313.132 376.328 313.123 376.423 313.132 376.328 0.0 0.0(1,2) 383.442 376.571 383.454 376.523 383.353 376.375 0.0 0.0(2,2) 454.120 377.058 453.841 376.704 453.496 376.422 0.1 0.1(3,2) 525.555 377.485 524.412 376.969 523.561 376.469 0.2 0.1(-3,3) 100.637 447.425 100.635 447.684 101.881 446.615 1.2 0.2(-2,3) 171.700 446.779 171.778 447.350 172.376 446.623 0.3 0.2(-1,3) 242.228 446.699 242.554 447.160 242.793 446.631 0.1 0.1(0,3) 312.906 446.869 313.111 447.113 313.132 446.639 0.0 0.1(1,3) 383.615 447.488 383.593 447.202 383.392 446.647 0.1 0.1(2,3) 454.514 448.123 454.136 447.420 453.574 446.655 0.1 0.2(3,3) 526.314 448.815 524.868 447.764 523.678 446.663 0.2 0.2

将同一行的点的各种坐标值绘在同一坐标系中，进行比较. 绘图如下：

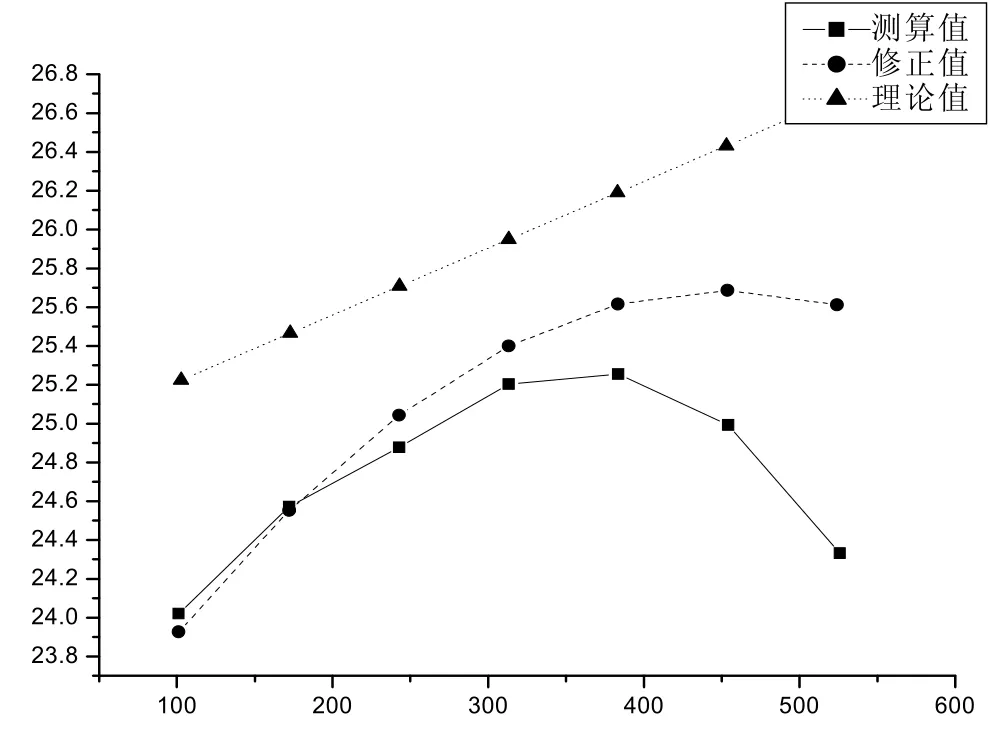
图5 第1行点阵

图6 第2行点阵

图7 第3行点阵

图8 第4行点阵

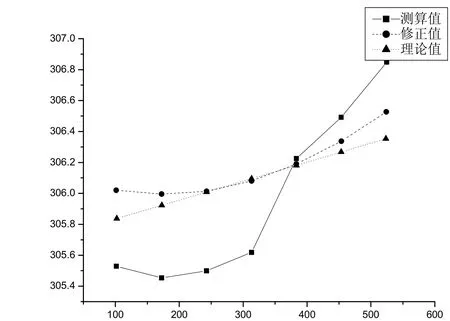
图9 第5行点阵

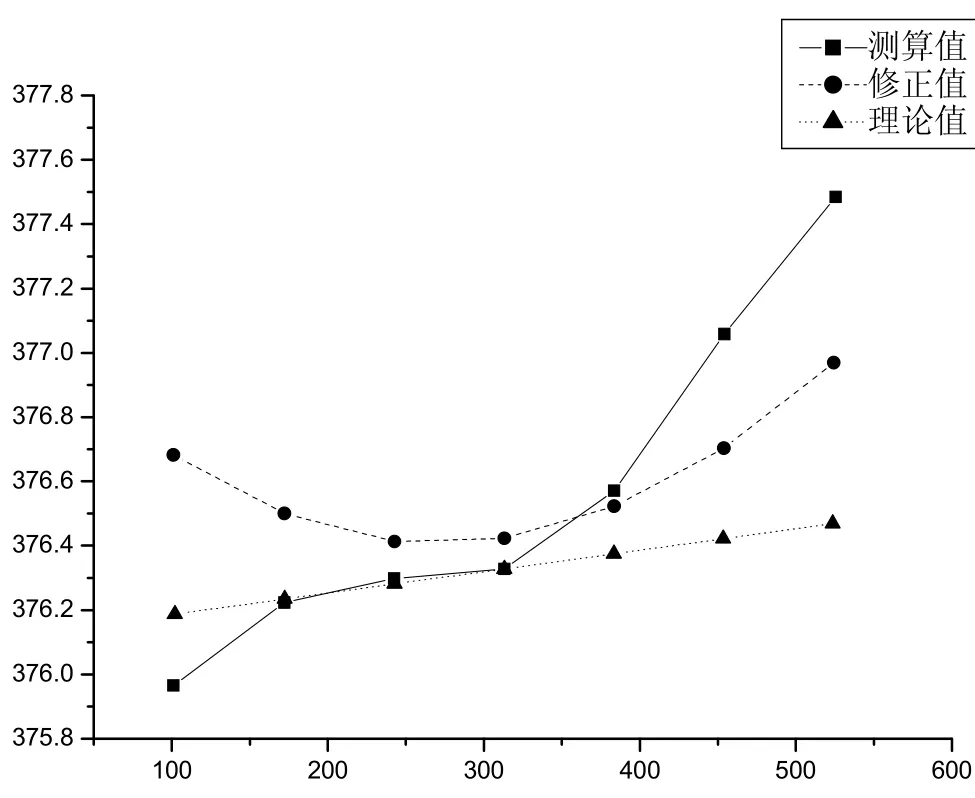
图10 第6行点阵

由图5-11可知，七行点阵中，位于中间的第四行误差最小，越远离相片中心点，误差越大；经过畸变误差修正后，点像坐标误差明显减小，如位于右下角的点误差从2个像素减小到1个像素.

玻璃折射光差的检定试验设计基本思想是：在光滑墙面上粘贴计算机生成的网格点图，用相机拍下像片；在贴图上附上玻璃，用相机拍下像片，比较两张像片；改变相机与墙面间距离，重复前面的步骤，对图片进行分析，并用式(3)(4)对拍摄的隔有玻璃的图片进行修正，比较修正效果. 具体操作为：

1)在光滑墙面上粘贴一横排黑点，直径为5 mm，间距40 mm，共有13个；

2)相机放置在排点的正对方向2.0m处，拍下照片，相机不动，在点上附一块厚度为8mm的钢化玻璃板，再次拍下照片；

3)拍摄纵距分别为2.0 m、2.5 m、3.0 m、3.5 m、4.0 m、4.5 m、5.0 m，重复步骤2).

因为像片拍摄过程中，按快门的力道晃动了镜头，因而，单从坐标的比较还看不出进行折射光差修正后坐标与无玻璃遮挡时坐标的关系，所以，下面选用了点间距平均值来比较.

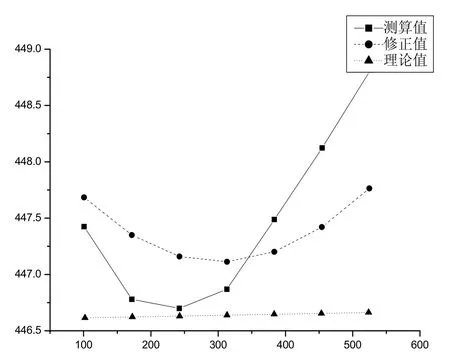
图11 第7行点阵

表2 点间距平均值比较

从表2列4可以看出，折射光差是与拍摄纵距基本呈反比关系，拍摄纵距越大，折射光差越小；通过对列6与列4进行比较可以发现，采用式(2)、(3)可以有效滤除折射误差.

3 结论

通过误差原因分析和试验研究，得出结论：

1)像片与实物相比具有一定程度的畸变，并且越靠近像片边缘，畸变越大；通过建立数学畸变计算模型，滤除畸变后，相对误差最大值仅有5.1%，86%的点位相对误差不足1%；

2)光线折射对坐标的影响与玻璃厚度、拍摄纵距及点坐标有关，通过建立数学折射误差计算模型，滤除折射误差后，相对误差小于0.3‰；

3)试验证明将数码相机应用于近景测量是可行的，在采用质量较好的数码相机，滤除误差后，相片失真可以得到很好的解决，误差较小. 与放射线测量法相比，数码相机安全无害；与高精度测量专用相机相比，普通数码相机操作简单、灵便，相信随着数码科技的发展，数码相机在测量领域中的应用前景非常广阔.

[1] 王之卓. 摄影测量原理[M]. 武汉: 武汉大学出版社, 2007.

[2] 张广军. 激光直边衍射CCD位移测量方法[J]. 实用测试技术, 1994, 2(6): 36-37.

[3] 罗先启, 陈海玉, 沈 辉, 等. 自动网格法在大型滑坡模型试验位移测试中的应用[J]. 岩土力学, 2005, 26 (2): 231-234.

[4] 任伟中, 寇新建, 凌浩美. 数字化近景摄影测量在模型试验变形测量中的应用[J]. 岩石力学与工程学报, 2004, 23 (3): 436-440.