飞艇系留系统静态与动态仿真研究

王亚伟 贾月红 陈智谦 韩雅慧 杨春信

（北京航空航天大学航空科学与工程学院，北京， 100191）

1 引言

系留飞艇可广泛应用于科学观测、空中预警、勘探侦查、抢险救灾等军民领域，具有生存能力强、成本低等优势[1-2]。而近年来，随着绳索在系留浮空器、空间系留卫星、海洋系留探测器等领域的大量应用，绳索力学已成为一般力学研究中的热点。绳索极度柔软，但又不属于标准的柔性体，具有只能承受拉力的物理特性，且为能量耗散体，这给动力学模型的建立和仿真分析带来了一定的困难。因此建立数学物理模型准确描述绳索特性成为研究的关键，对于离散的绳索仿真模型，通常情况下采用多刚体模型或阻尼弹簧模型。Banerjee应用多刚体假设建立了“船-电缆-水下探测器”的动力学模型[3]；Djerassi等人建立了绳索从2个移动平台拉出的多刚体模型[4]；文献[5]采用多刚体模型分析了飞艇-绳索-子弹系统动力学问题；Frost采用阻尼弹簧模型模拟了2个由绳子连接2个弹的高空抛撒过程[6]；文献[7]应用阻尼弹簧模型模拟了系留气球的升空过程；文献[8]应用阻尼弹簧模型研究了绳索-灵巧子弹的动力学特性；国防科技大学硕士学位论文中采用“珠式模型”模拟了空间系留卫星的收拢、释放以及保持过程，其中将绳索部分处理成质点-弹簧-阻尼单元模型[9]。

本文应用ADAMS对飞艇系留系统进行静力学和动力学仿真，建立了绳索的阻尼弹簧模型，针对不同风速条件、驻空攻角以及绳索质量，分析了系留缆绳在静态和动态状况下的内部张力和姿态变化。

2 数学物理模型

飞艇系留系统由飞艇和绳索组成，建立飞艇系留系统仿真模型前需作出如下假设：假设绳索与飞艇质心相连接，所受外力均作用在质心上；不考虑飞艇外形及姿态的变化，将其视为质点；不考虑风场随高度的变化。

本文使用多体动力学分析软件ADAMS建立仿真模型，系统中绳索连接地面和飞艇，将绳索离散为若干个绳段，质量集中在各绳段上端。在软件中以小球表示质量点，顶端质点质量为顶端绳段与飞艇质量之和，其余质点质量即为绳段质量；质点间施加弹簧力，自定义弹簧力大小使其只承受拉伸力，并考虑弹簧的阻尼作用。除自重以外，在O-XY平面内考虑绳索所受气动力以及飞艇所受气动力和浮力，并将外力施加在相应质点上。

2.1 飞艇受力分析

除自重以外，在O-XY平面内考虑飞艇所受气动力和浮力，受力分析如图1所示。

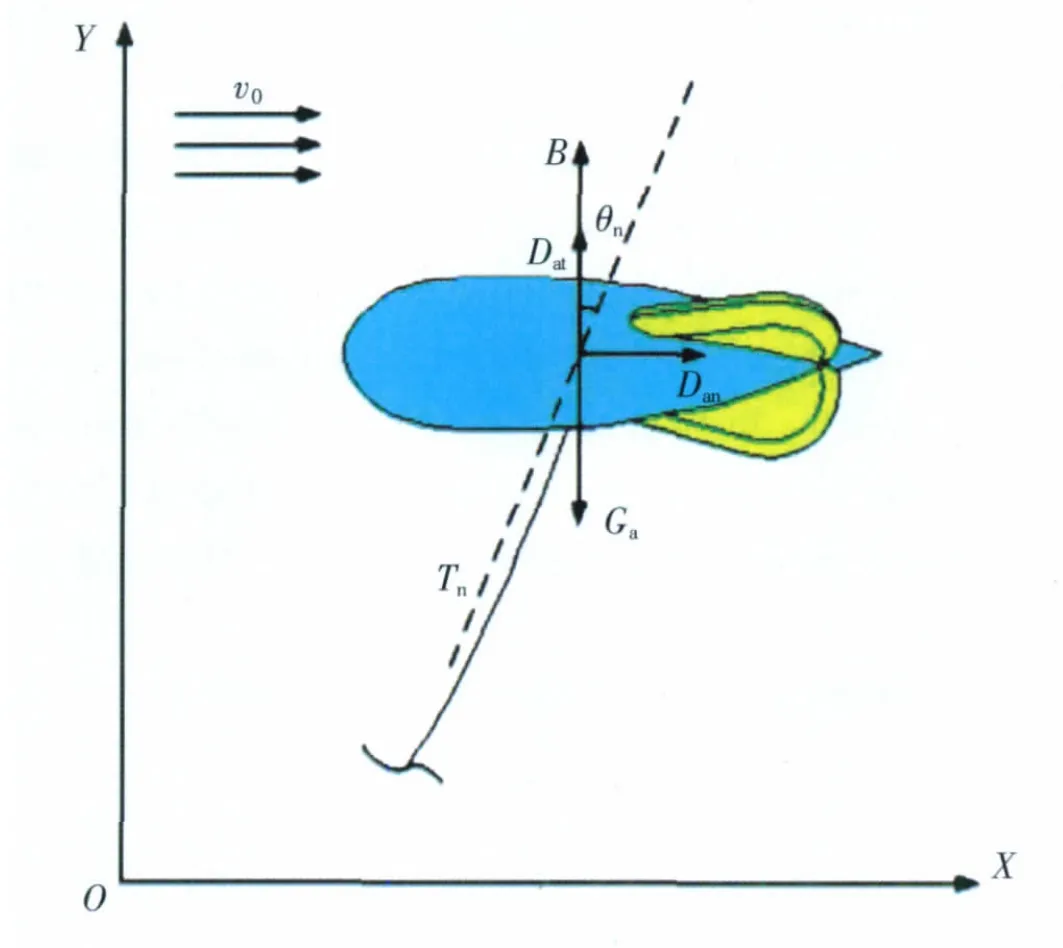
图1 飞艇受力分析Fig.1 Forces analysis of airship

图1中v0为当地风速；Ga为飞艇重力；θn为与飞艇连接的绳段与竖直方向的夹角；Tn为绳索对飞艇的拉力，用来平衡飞艇所受外力；B为飞艇所受浮力，按照式（1）计算；Dat、Dan分别为飞艇所受切向气动力和法向气动力，分别按照公式（2）、（3）计算。

式中 ρair为相应高度下的大气密度；Va为飞艇的体积。

式中 S为飞艇参考面积；Cat、Can为飞艇相应方向的气动力系数，对于相同飞艇，此值受其空中姿态的影响，本文中所使用的气动力系数由FLUENT数值计算获得；v为飞艇相对于气流的速度，在静力学分析中v=v0，动力学分析中还要考虑飞艇质心的运动速度。

2.2 绳段受力分析

图2 系留缆绳受力分析Fig.2 Forces analysis of tether

系留缆绳受力分析如图2所示，质点用mi表示，θi为第i个绳段与竖直方向的夹角。在绳索的质点-弹簧模型中，质点分别受前后弹簧的拉力作用，用Ti表示；Gs为绳段重力；Ds为绳段所受气动力，按照经验公式（4）、（5）计算：

式中 Dst、Dsn分别为绳索所受切向气动力和法向气动力，相应的气动力系数一般由实验方法获得，本文中按照文献[10]所给出的经验公式，根据问题的雷诺数范围取Csn=1.27，Cst=0.062；d为绳索直径，l为绳段长度。将气动力分解为x，y方向，沿绳索切向的气动力较小，在此忽略不计，则有：

3 仿真结果

本文研究对象为系留热气飞艇，驻停高度在1～2km范围内；飞艇长度54m，体积约6 400m3；自身质量约280kg，负载约为686kg，布置在囊与系留绳之间，在仿真建模时将飞艇和负载视为同一质点；绳索总长2km，将其划分为10个等长片段建立质点弹簧模型。

3.1 静力学分析

对于同一个飞艇产品，影响飞艇驻空高度、偏移距离的因素主要有风速以及飞艇的驻空姿态。本节针对不同风速和不同的驻空攻角进行静力学分析，关注绳索姿态以及拉力分布，此外还考虑了绳索质量对仿真结果的影响。

本文在飞艇攻角为0～12°、风速为5～15m/s、绳索线密度为0.089～0.356kg/m范围内选取共8个工况进行仿真计算，各工况具体参数如表1所示，其中总上升力包括浮力和气动升力，总阻力为气动阻力。

?

按照工况表中所列工况进行计算，得到结果如下：在攻角为0°的情况下改变风速，得到绳索中张力分布曲线和绳索形态图，如图3、4所示。

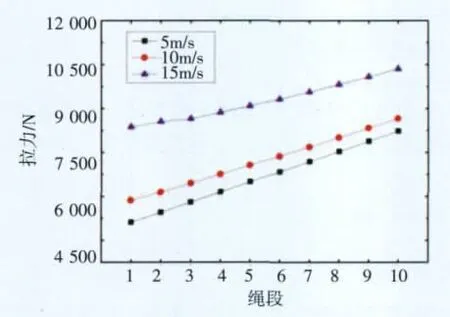
图3 不同风速下的系留绳张力分布曲线Fig.3 Tension distribution in various wind velocity

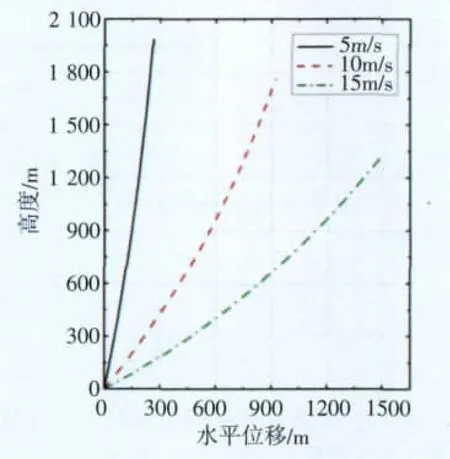
图4 不同风速下系留绳形态图Fig.4 System state in various wind velocity

由图3可见，绳索中的拉力分布不均匀，从地面沿绳索向上绳索张力逐渐增大，在绳索与飞艇的连接处达到最大值。由受力分析可知，连接飞艇绳段所受的张力大小和方向是由飞艇所受外力决定的，以下的每个绳段受前后绳段的拉力来平衡自身所受的外力作用，由于上部的绳索与竖直方向的夹角较小造成气动阻力较大，从而需要更大的绳索张力来平衡外力。

此外，如图3、4所示随着风速的增大，绳索的水平偏移量增大，相应地飞艇的驻空高度降低，且绳索的弯曲程度有所变化；绳索张力增大，且分布规律有所改变，这是由于气动力的改变造成的。风速从5m/s增加到15m/s的过程中，飞艇高度降低34%，绳索最大拉力增大26%。

在风速为10m/s的情况下，改变飞艇驻空攻角，从而引起飞艇升阻比的变化，得到4种攻角下的绳索张力分布曲线和绳索形态图，如图5、6所示。

图5 不同飞艇攻角下的系留绳张力分布曲线Fig.5 Tension distribution in various attack angle

图6 不同飞艇攻角下系留绳形态图Fig.6 System state in various attack angle

在图5中，绳索张力大小在一定的攻角范围内随驻空攻角的增大而增大，这是由于飞艇所受的外力增大，从而对绳索的拉力增大。此外，由图6所示的绳索形态可以看到，随攻角增大飞艇的驻空高度增加，同时水平偏移量减小，这主要是受飞艇升阻比的影响，在一定范围内，随着攻角的增大，飞艇升阻比逐渐增加，由受力平衡关系决定了飞艇的驻空位置向上移动。在攻角从0°变化到12°的过程中，飞艇驻空高度仅增加9%，而绳索拉力增大两倍。

在攻角为0°，风速10m/s的情况下，改变绳索线密度，得到不同质量下的绳索张力分布曲线和绳索形态图，如图 7、8所示。

图7 不同线密度下的系留绳张力分布曲线Fig.7 Tension distribution in various linear density

图8 不同线密度下的系留绳形态图Fig.8 System state in various linear density

在这里分析绳索质量对飞艇系留系统的影响，主要是考虑在绳索材料一定的情况下，加大绳索强度必然会引起质量的增加，而系统设计时既要考虑系留性能又要保证系统的安全。由图7、8可以看到随着绳索质量的增加绳索的形态发生了变化，当质量达到一定程度时绳索会发生明显弯曲，此时绳索中张力分布不均匀程度加大，但绳索中的最大拉力差别在6%以内；同时飞艇的水平偏移量增大，在绳索质量增大4倍的情况下驻空高度降低约20%。

3.2 动力学分析

由于实际情况下风场是不稳定的，飞艇驻停过程不是一个稳定的状态，会出现摆动的现象，摆动过程中飞艇的位置和绳索的形态均会发生变化。本节针对此问题进行飞艇系留系统动力学分析，计算飞艇的摆动过程。

动力学仿真模型在静力学模型的基础上考虑了飞艇和绳段质心的运动速度，假设风场按照正弦规律波动，本文中风速按照式（8）计算，即假定风速在10m/s上下波动，振幅为5m/s，周期为10s。针对攻角为0°，绳索线密度0.178kg/m的工况进行仿真分析，绳索初始位置设为竖直，运行500s的仿真，观察飞艇的运动过程。

式中 t为仿真时间。

结果显示，在变风场条件下，飞艇在波动过程中逐渐趋近静平衡位置，如图9、10所示，图9为飞艇系留系统的位置随时间变化图，图10为与地面连接和与飞艇连接的绳段内部张力随时间变化曲线。将整个仿真过程分为3个阶段，即快速移动阶段、缓慢移动阶段和驻停阶段，如图10所示。0～200s为快速移动阶段，在此阶段飞艇由静止状态在外力作用下开始运动，运动过程中偏移速度较大，振幅、周期均不稳定；200～400s为缓慢移动阶段，在此阶段飞艇在稳定的波动中缓慢向平衡位置移动，具有较稳定的振幅和周期；在400s之后系统基本达到静平衡位置，称为驻停阶段，在此阶段飞艇在静平衡位置附近往复摆动，绳索姿态也随之出现稳定的波动现象，图11为对应图10中驻停阶段的放大图。

图9 飞艇系留系统的位置随时间变化图Fig.9 Transient state of tether

图10 连接飞艇/地面绳段内部张力随时间变化曲线Fig.10 Transient tension of the top and the bottom segment

图11 驻停阶段绳段内部张力变化曲线Fig.11 Transient tension of the segments when staying

可见气流的波动造成了系统运动状态的变化，导致绳索内部张力发生波动。在飞艇逐渐达到平衡位置的过程中绳索最大拉力达到了9 895N，比静平衡点高出约15%；如图11所示，绳索在平衡位置附近波动过程中最大拉力在9 215～8 123N之间波动，振幅约为1 000N，周期10s；底部绳段张力的振幅略大于顶部，在6 476～5 262N之间波动；相应地，飞艇的驻空高度和偏移距离都有较小的变化，在此工况下，飞艇的驻空高度在1 766～1 755m之间波动，偏移距离在937～915m之间波动，可以说波动范围不大。需要说明的是，实际风场的变化是一个较为复杂的过程，本文以简单的正弦波代替，主要通过仿真定性观察风场的变化对飞艇系留系统性能的影响。

4 结束语

本文基于多体动力学软件ADAMS建立了飞艇系留系统仿真模型，将绳索处理为质点-弹簧-阻尼系统，在不同风速、驻空攻角以及绳索质量条件下，针对某型飞艇产品进行了8个工况的静力学和1个工况的动力学仿真分析，得到主要结论如下：

1）张力从地面沿系留绳逐渐增大，在与飞艇连接处达到峰值，因此系留绳与飞艇的连接要保证足够强度；

2）随着飞艇攻角的增加，飞艇的驻空高度增加，偏移量减小，但绳索内部张力也有显著的提高，因此选择驻空攻角时应根据绳索强度和任务需求权衡；

3）绳索的质量对飞艇系留系统的影响较大，因此在保证强度的前提下应尽量选取轻质绳索；

4）在风的作用下飞艇会发生水平偏移，随着风速的增加，飞艇的水平偏移量增大，驻空高度降低，在变风场条件下，绳索内张力发生波动，但波动范围不大，建议在选择绳索最大拉力时考虑一定的安全系数，以保证在飞艇的不断运动过程中的安全运行。

（

）

[1]卢新来，罗明强，孙聪.系留气球的升空模拟[J].航空学报，2006，27（5）：768-772.

LU Xinlai， LUO Mingqiang， SUN Cong.Simulations of Tethered Balloon Ascent[J].Acta Aeronautica et Astronautica Sinica，2006，27（5）：768-772.（in Chinese）

[2]葛强林，葛强胜.飞艇在执行多样化军事任务中的作用[J].国防交通工程与技术，2011（2）：4-6.

GE Qianglin，GE Qiangsheng.On the Roles of Airships in Carrying Out Various Military Tasks[J].Traffic Engineering and Technology for National Defense，2011（2）：4-6.（in Chinese）

[3]Banerjee A K.Deployment Control of a Cable Connectinga Shiptoan Underwater Vehicle[J].Journal of Guidance，Control，and Dynamics，1994，17（6）：1327-1332.

[4]Djerassi S， Bamberger H.Simultaneous Deployment of a Cable from Two Moving Platforms[J].Journal of Guidance， Control， and Dynamics，1998，21（2）：271-276.

[5]唐乾刚，王振国.飞艇-绳索-子弹系留动力学研究[J].国防科技大学学报，2008，30（4）：28-32.

TANG Qiangang，WANG Zhenguo.A Research of Tether Dynamics in Airship-towed System[J].Journal of National University of Defense Technology，2008，30（4）：28-32.（in Chinese）

[6]Frost G， Costello M.Two Projectiles Connected by a Flexible Tether Dropped in the Atmosphere[J].Journal of Guidance，Control，and Dynamics，2000，23（6）：1081-1085.

[7]史献林，余莉，施红.系留气球升空过程的动态模拟[J].航空学报，2009，30（4）：609-613.

SHI xianlin，YU li，SHI hong.Dynamic Simulation of Ascending Tethered Balloon[J].Acta Aeronautica et Astronautica Sinica，2009，30（4）：609-613.（in Chinese）

[8]郭良，唐乾刚，张青斌.飞艇系留试验中的绳索动力学研究[C].2007年第九届全国振动理论及应用学术会议论文集，杭州：2007.

GUO Liang，Tang Qiangang，Zhang Qingbin.The Research of Tether Dynamics in Airship-towed System[C].Proceedings of The 9th National Conference on Vibration Theory and Application，Hangzhou： 2007.（in Chinese）

[9]李强.空间绳系卫星系统动力学建模及仿真研究[D].长沙：国防科技大学硕士学位论文，2007.

LI Qiang.Study on Space Tethered Satellite System Dynamic Modeling and Simulation[D].Changsha： Master's Thesis，National University of Defense Technology，2007.（in Chinese）

[10]休斯敦R L，刘又午.多体系统动力学下册[M].天津：天津大学出版社，1991.

Huston R L，LIU Youwu.Dynamics of Multi-Body Systems[M].Tianjin：Tianjin University Press，1991.（in Chinese）