专用车辆系统结构振动特性分析

孙志春，周志立，李 言，谢基龙，谢云叶

(1.西安理工大学机械与精密仪器工程学院，陕西西安710048;2.济宁职业技术学院，山东济宁272037;3.河南科技大学车辆与动力工程学院，河南洛阳454900;4.北京交通大学机械与电子控制工程学院，北京100044)

由大量的刚体和控制单元组成的机械和车辆多体系统的动态问题可用相关的多体系统软件进行有效的研究分析。但随着车辆高速化、重载化以及结构轻量化的不断发展，越来越要求能准确合理可靠地处理系统中的弹性体结构，并对其进行非线性动力学分析;在此基础上建立刚柔耦合的车辆系统动力学模型，对车辆系统的结构振动进行更为精确、快速的计算分析。在已发展和建立起来的多个基于物体小弹性变形的多体分析方法中，变形可表示为随空间振型和时间变化的模态坐标的线性组合，振型可通过解析解或有限元方法获得。

进行多体系统仿真分析，应首先建立多体系统运动方程的矩阵。对于可将物体模拟为具有解析解的简单弹性体情况，理论已比较完善［1，2］。而对形状复杂且无解析解的弹性体，可采用有限元方法计算的结果，来获取弹性体特征的描述信息并形成多体系统软件中表示弹性体的标准信息［3，4，5］，为构成系统方程的矩阵做准备。

由于车辆多体系统动力学分析受自由度数目的限制，直接用有限元模型处理其中的弹性体，会导致系统自由度太多，不宜于多体系统的建模与求解。因此，文章采用超单元法来缩减处理某专用车辆多体系统中弹性底架，建立有“动特征”的底架弹性体模型，使得求解的自由度数大为减少又不失精确性。在此基础上，通过引入车辆系统中的其他非线性因素建立了该种车辆的刚柔耦合动力学模型，并计算分析了车辆系统的结构振动特性，及运行速度等参数对车辆结构振动的影响。

1 车辆多体系统中弹性体运动学分析原理

在多体系统中的任一弹性体可通过连接元件与其它物体连接。各物体间的作用力和力矩由这些连接元件表示，同时还应考虑作用于表面的面力和由重力等因素引起的体积力。为说明弹性体的运动状态，在此使用三种广义坐标系(见图1)。第一种是惯性坐标系{OI，eI}(OI是原点，eI是惯性坐标系的单位矢量;以下类同)，来确定物体的方位。第二种是参考坐标系{Oi，ei}，它固定于弹性体上，相对上述惯性坐标系建立的。第三种是弹性变形坐标系{Pi，ei}，它相对于上述参考坐标系而建，可使用物体的有限元模型。

现考虑图1中所示的任一弹性体i，在参考坐标系中求解所有的量。图中状态变量ri、Ai、vi和wi分别表示参考坐标系的位置、方向、线速度和角速度。对于固定于弹性体上的参考坐标系，相对于惯性坐标系做大的运动，可由位置矢量ri和方向矩阵Ai描述出来。而物体的相对变形可用相对于参考坐标系由矢量定义的任意材料点P的运动来描述。在小变形情况下，物体的运动和动态方程可相对于其初始状态按一阶泰勒展开式进行线性化处理。对于物体上各点的变形，可以通过相对坐标系的方向矩阵和位移矢量来计算。在上述基础上，弹性变形坐标系相对于惯性坐标系的运动就可以描述出来。

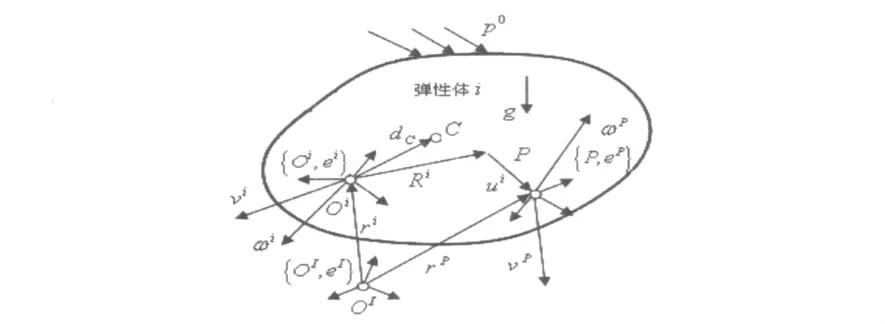
图1 弹性体坐标系Fig.1 Coordinate system of a elastic body in multibody system

2 车辆多体系统中弹性体变形有限元分析与运动方程

由于结构上的复杂性，对多数弹性体，很难用连续简化模型来精确表示，所以用更一般的有限元程序计算求出标准信息，再由多体系统中的前处理器来读取有限元软件程序的计算结果并计算标准信息文件。众多算例已经表明，对多体系统中具有复杂几何形状和复合材料特性的弹性体，用有限元法先行计算分析弹性体的模态等固有动态特性是可行的，以获取多体系统中所需的振型等信息。

2.1 车辆多体系统弹性体变形的有限元分析

由机械振动理论可知［8］，静态振型和特征振型是相互正交的。由式(4)可见，弹性体变形既可通过静态振型求解也可通过特征振型计算，可大大缩减计算自由度，方便弹性体的计算。而通用的有限元程序可处理任意形状和材料特性的弹性体，因而结合有限元法，将大大拓宽多体系统的运用范围。

2.2 弹性体运动方程

基于以上分析，结合约旦虚功原理和达朗伯原理，利用有限元分析可得出弹性体的运动方程。在有限元分析中，可通过求解下式(5)来计算结构特征值:

求出的nq个特征振型ΦJm可用矩阵ΦJ表示，即:ΦJ=［ΦJ，……，ΦJnq］。

根据以上有限元分析得出的特征振型矩阵ΦJ、质量矩阵MJ、刚度矩阵KJ以及几何刚性矩阵KσJ完成下面的模态转换:

进而可得出弹性体i的运动方程。另外，弹性体有限元坐标X可通过由有限元建立的一组对应的解耦广义坐标Xj和振型矩阵:ΦJ变换得出，即:X=:，将其按泰勒展开，取前两项:

把上面对弹性体的有限元分析结果(结构和特征信息)通过多体系统程序读入，并经过转换形成多体系统中所需的标准输入数据文件，结合多体系统中其它因素的处理即可建立刚柔耦合的多体系统模型，进而进行动态仿真和计算分析。

3 车辆多体系统中弹性底架的模态分析

某型专用车辆中的底架是直接装载货物的承载部件，相对系统中的其他构件，其结构长，运行中弹性问题突出，因而需要把它考虑为弹性体。其为箱型钢板焊接结构，在此采用四边形板单元shell63对其进行有限元建模(有限元模型如图2所示)。模型中各部分结构和尺寸完全按照其结构实际情况，网格划分要求几何形状与原结构一致，并疏密结合，这样既可以减少节点数、提高计算效率，又可以保证计算精度。

为在多体系统分析中能反映出底架的振动特性，须对其的固有动态特性进行详细分析，因而有必要对底架有限元模型进行模态分析。在此采用兰索斯法分析弹性构架的模态，计算其前20阶模态，得到了各阶固有频率及振型。由于在实际运用中底架主要承受低频载荷［9］，高频率的振型对结构振动响应的影响很小，可以忽略。因此取其中前8阶模态来做分析，结果见表1。

图2 底架有限元模型Fig.2 Finite－element model of the chassis underframe

由于弹性底架结构比较复杂，同时考虑到系统动力学分析中对自由度数目的限制，用有限元超单元法［10］建立底架弹性体有动特征的模型，使描述底架的节点数和自由度数大为减少，但又不失计算结果的准确性，达到即缩减模型自由度又提高计算效率的目的。

在此采用Guyan缩减法将弹性矩阵问题缩减为一个较小主自由度集矩阵问题。由于缩减质量矩阵的精度取决于主自由度的位置和数目，所以对于较复杂的底架在手动选择一部分主自由度的同时，也让有限元程序自动选择一些自由度，这样可弥补可能被遗漏的模态点。这里将整个底架作为一个超单元来处理，共选取了236个主节点，共1416个主自由度。

对生成的底架超单元进行模态求解，得到的模态解与振型(也取前8阶)见表1。比较用超单元与有限元模型计算出的底架模态结果，可见在前8阶内弹性振型频率最大相对误差为0.83%。由此可见，用超单元法计算的底架模态结果精度是足够高的，且通过实际应用表明能满足车辆系统振动分析要求。

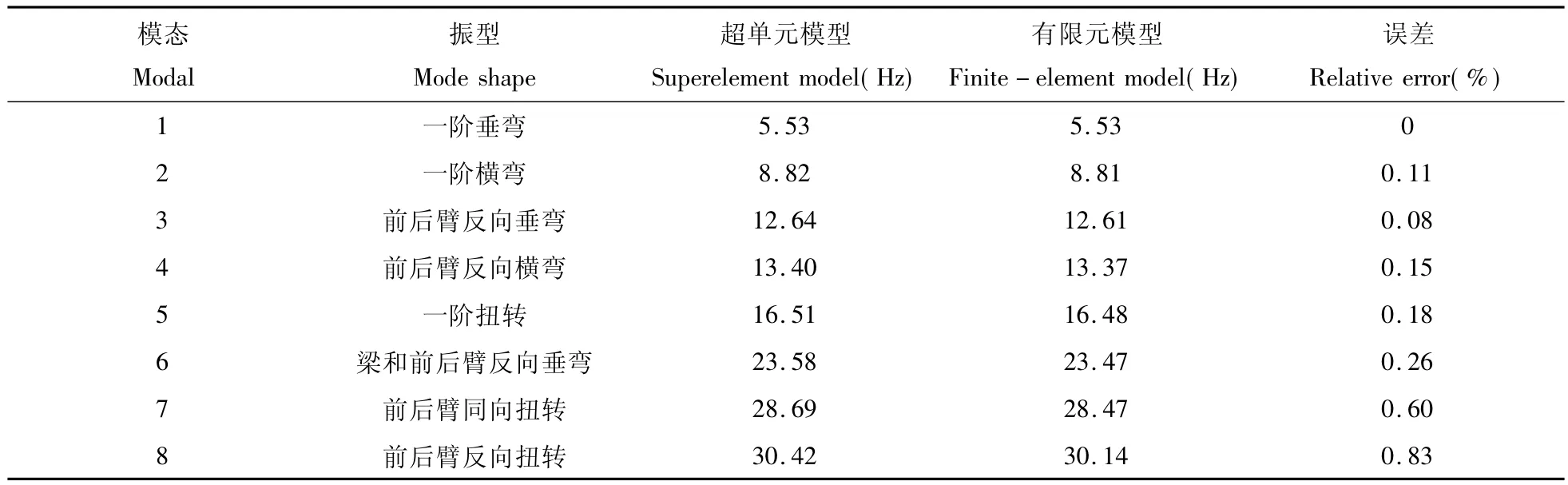
表1 底架有限元及超单元模型模态计算结果Table 1 Calculated modal results of the finite－element model and superelement of the chassis underframe

4 应用

基于上面的分析，将底架的弹性信息输入到多体系统中实现对其的弹性模拟，在对所关心的因素进行合理处理后，建立了含有该底架弹性体的刚弹耦合的车辆多体系统动力学模型(见图3)，并进行了计算分析，获得了几种典型运行速度下车辆系统的振动响应。在选取的参考点上，将不同速度下的模拟计算结果——垂向加速度(见图4，在此仅列出60 km/h和80 km/h两种速度下的历程)与实验结果进行比较(见表2，表中列出了五种速度下的结果)。表2中，g为重力加速度。

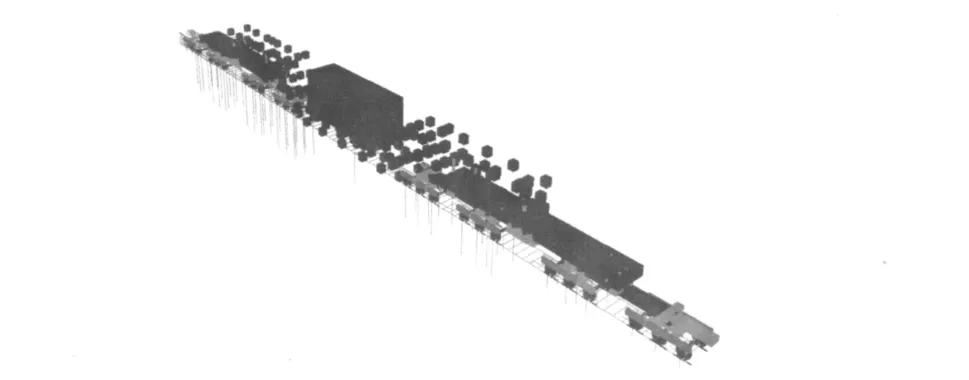
图3 专用车辆系统刚柔耦合动力学模型Fig.3 Rigid－flexible coupling dynamics model of the special vehicle system

通过分析结果，可以看出在将底架作为弹性体考虑后，参考点处的模拟计算结果与实测结果基本吻合，误差都没有超过3.77%。因而，可以满足工程需要，能对该车辆系统振动特性进行可靠分析。通过分析，还可以看出，在60 km/h～100 km/h之间振动加速度在90 km/h上下时有一极大值;主要原因是:在此速度上下运行时，线路形成的激扰频率与车辆的底架一阶固有频率相接近，因而应避免在此速度上下运行。

图4 不同速度下参考点处的振动响应Fig.4 Vibration responses on selected point under different velocities

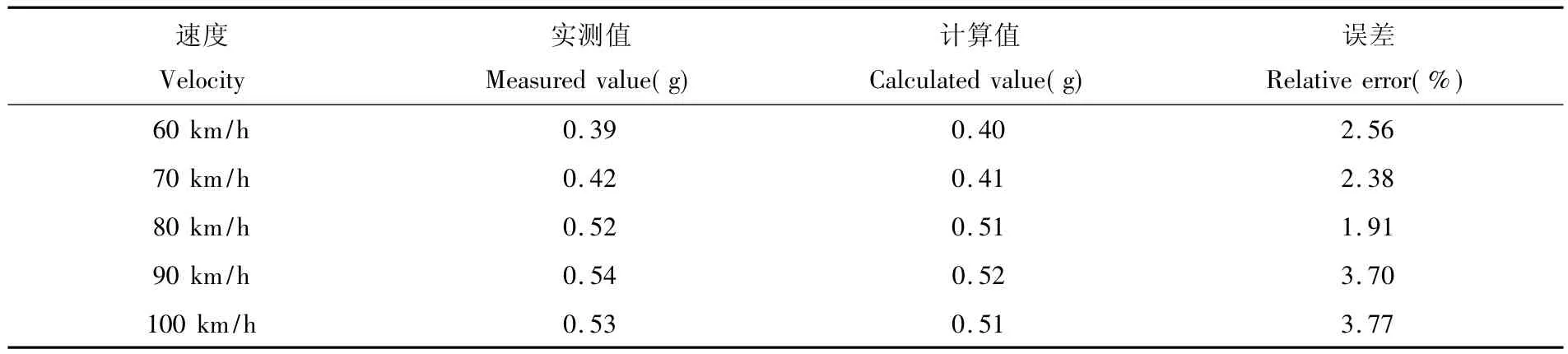
表2 几种速度下模拟计算值与实测值及其比较Table 2 Measured values，calculated values，and their relative errors under different velocities

5 结论

为精确和快速地分析车辆系统的振动特性，文章将多体系统与有限元理论相结合，研究分析了弹性体在多体系统中的运动学描述、变形和运动方程，以及用有限元法描述弹性体特征的方法，为在多体系统中精确和快速地处理弹性体奠定了理论基础。

以上述分析原理为基础，采用了超单元法对专用车辆系统中的底架进行处理，建立了有动特征的底架弹性体模型，使所描述底架的自由度减少，因而大大缩小了计算规模，同时又保证了结果的精确性。结合车辆中其他所关心因素的合理处理，建立了该种车辆系统的刚柔耦合动力学模型，并计算分析了典型速度下车辆系统的振动特性。

计算分析结果表明，在感兴趣的频率范围内底架各弹性振型频率的最大误差为0.83%;且在参考点处，典型运行速度下，该车辆系统振动模拟结果与实测值接近，最大误差不超过3.77%。因而，这种放处理方法的精度是十分高的，也是可靠的，能满足工程系统结构振动分析的需要。振动加速度在90 km/h上下时有一极大值，为保证车辆运行安全，应避开此速度。

［1］Shabana AA，Wehage RA.A coordinate reduction technique for transient analysis of spatial structures with large angular rotations［J］.J.Struct.Mech，1983，11(3):401 －431

［2］O.Wallrapp.Flexible bodies in multibody system codes［J］.Vehicle system dynamics，1998，30:237 －256

［3］O.Wallrapp.Standardization of flexible body modeling in multibody system codes，Part I:Definition of standard input data［J］.Mechanics of structures and machines，1994，22(3):1994，283 －304

［4］李东平，曾庆元，娄 平.车辆多体系统动力学方程的有限元方法［J］，中国铁道科学，2004，25(5):10:34－38

［5］谢云叶，谢基龙，杨广雪，等.基于改进剩余柔度矩阵的自由界面模态综合法［J］，北京交通大学学报:自然科学版，2008，32(4):28－32

［6］Ali H.Nayfeh and P.Frank Pai:Linear and nonlinear structural mechanics［M］.Published by John Wiley ＆ Sons，Inc.，Hoboken，New Jersey，2004

［7］O.Wallrapp，A.Eichberger，and J.Gerl.FEMBS － An interface between FEM codes and MBS codes.User Manual for ANSYS，NASTRAN，and ABAQUS，INTEC GmbH，Wessling，Report Version 3.0，January 1997

［8］W.S.Yoo and E.J.Haug.Dynamics of articulated structures，Part I:Theory［J］.Journal of structures and mechanics，1986，14(1):105 －126

［9］S.L.Grassie.Models of railway track and vehicle/track interaction at high frequencies:Results of benchmark test［J］.Vehicle system dynamics supplement，1996，25:243 －262

［10］曾 攀.有限元分析及应用［M］.北京:清华大学出版社和Springer，2004