ADAMS参数化分析在高压压气机调节机构设计中的初步应用
2012-07-14杨伟,徐伟
杨 伟,徐 伟
(中国燃气涡轮研究院,四川成都610500)
1 引言
高压压气机多采用多级可调静叶来控制航空发动机的喘振和失速[1,2],使得用于调节可调静叶角度的多级联调机构显得十分重要。联调机构由多种典型构件组成,包括活塞、曲柄、连杆等,且每种构件及其几何参数对调节角度的精度都会产生较大影响。在联调机构方案设计阶段,不仅要确定机构的形式,还要充分考虑各种参数对调节角度的影响,使得最终设计不但能满足机构的功能性要求,而且调节角度精度较高。
本文介绍了某高压压气机三级联调机构在方案设计阶段基于ADAMS平台建立的简易模型,利用软件参数化分析模块(包括设计研究、试验设计和优化分析)研究了模型中重要的设计变量,及各优化目标约束下各设计变量的最优量值,并将模型优化分析结果用于调节机构虚拟样机的建模及分析。
2 调节机构分类
根据作动筒中活塞到联动环的运动传递方式,将多级联调机构分为曲柄连杆机构、曲柄轴机构和铰链梁机构三类。
(1)曲柄连杆机构。这种机构占有空间相对较小,特别适合2级或3级可调方案。同时,机构中采用对称放置两套液压作动筒,有效减小了系统变形;采用可调节长度连动杆,可单独控制每级静叶的调节角度。
(2)曲柄轴机构。高效节能发动机高压压气机中采用了这一调节机构[3]。这种机构适合多级可调静叶(特别是4~6级),对静叶调节规律在级与级间变化方面适应性强、曲柄轴刚性好、在V形点处联动环的侧向载荷最小。但整个系统轴向长度较长,质量较大,要求机匣外的空间也相应较大,且一般只采用一个液压作动筒进行驱动,整个系统变形较大。
(3)铰链梁机构[4]。与曲柄轴机构较类似。这种结构有利于机构合理运动,且是一种力的放大(省力)结构,铰接定位点之间的距离可根据调节角度范围而确定。但主梁(杠杆)太长,对空间要求较高。
3 调节机构方案设计
某高压压气机进口导流叶片(IGV)、第一级静子叶片(S1)和第二级静子叶片(S2)设计为可调叶片。为满足静叶角度调节和受力要求,在压气机机匣外设计了一套调节机构,对三级可调静叶实施联调。调节机构方案以曲柄连杆机构为基础进行设计:曲柄、联动环、摇臂及机匣通过连动杆和向心关节轴承连接,构成曲柄连杆机构,运动原理简图见图1[5]。
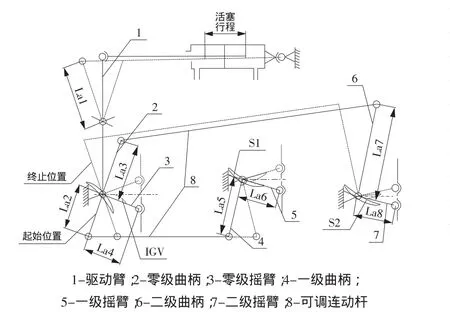
图1 机构原理简图Fig.1 Mechanism principle sketch
4 调节机构简易模型
为简化计算,只选取一套调节机构进行建模和仿真。基于ADAMS的简易模型包括液压作动筒,驱动臂,零级曲柄,一级曲柄,二级曲柄和一、二级连动杆。其中,驱动臂和零级曲柄作为一个零件考虑。建模步骤如下:
(1)创建设计变量。使用设计变量定义参数变量,建立设计变量和模型对象的关系。19个设计变量及其物理含义对照如表1所示。
(2)创建设计点。在模型中创建机构的关键位置点,以便建模和仿真分析。
(2)创建构件。利用零件库中的实体创建命令,建立圆柱体、球体、连杆等实体,并通过设计点联系,如图2所示。
(4)添加约束。模型中的运动副约束包括转动副、球副和固定副。机构中17个约束类型及位置如表2所示。

表1 设计变量与物理含义对照表Table 1 Design variables and physical definitions
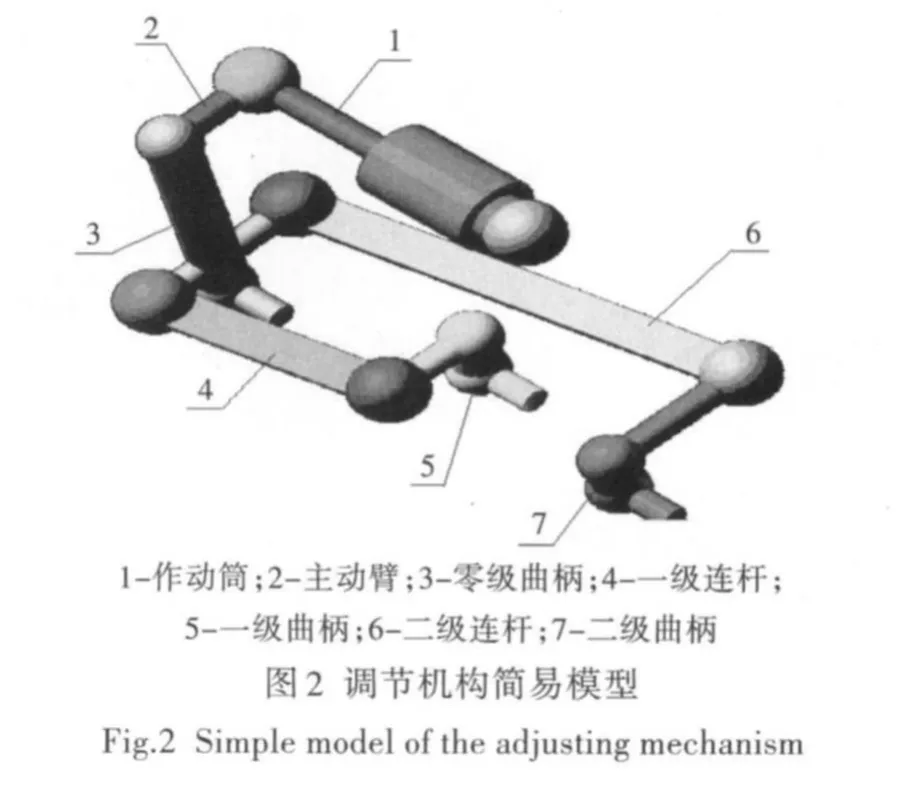
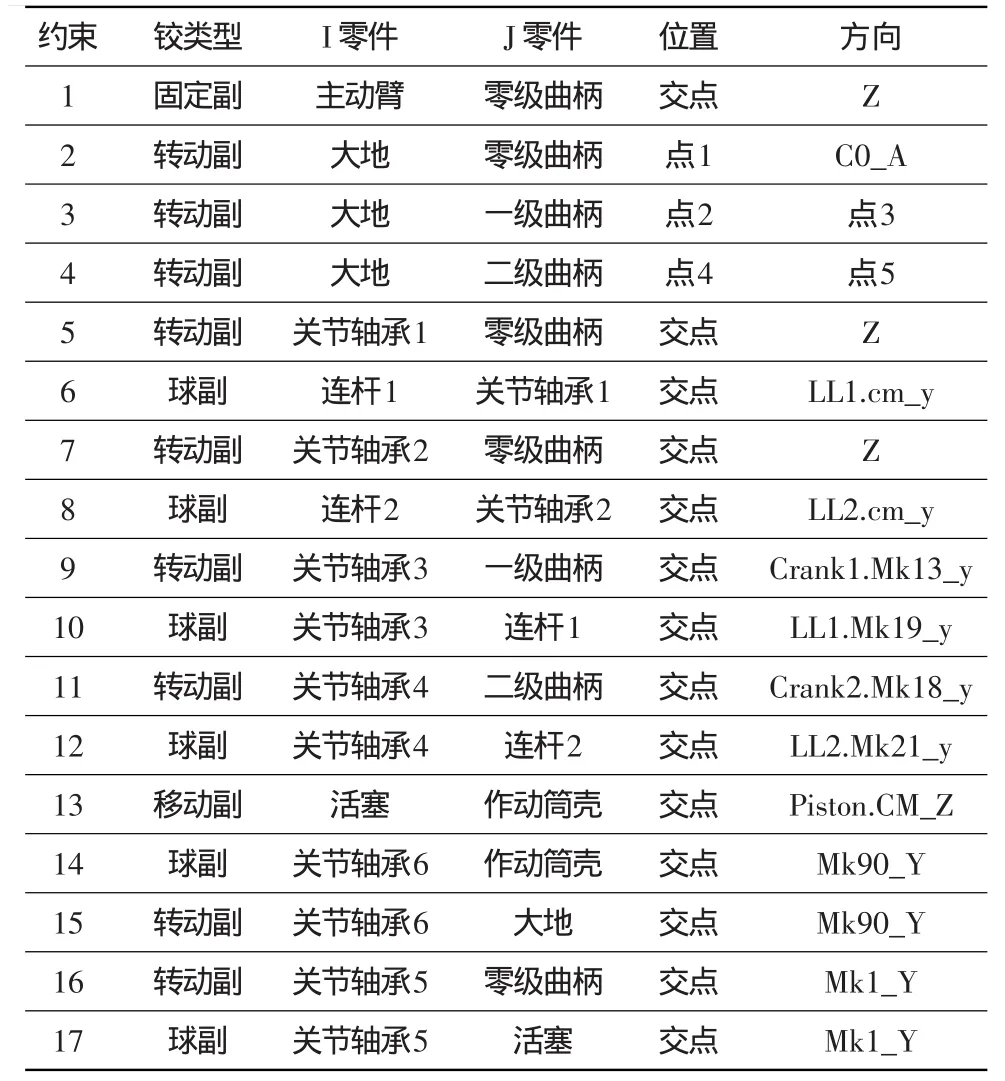
表2 模型约束类型Table 2 Joint types used in model
5 调节机构参数化分析
对调节机构进行参数化分析,可得各参数对调节角度的敏感度,并找出各设计变量的最优组合。
5.1 设计研究(design study)
主要研究内容为:如果某个设计变量发生变化,样机的性能将如何变化。通过设计研究,用户可获得以下信息[6]:
(1)在设计变量变化范围内,样机有关性能的变化情况;
(2)在指定参数变化范围内,找出最佳的设计参数值;
(3)样机有关性能对设计参数变化的敏感度。
在调节机构的设计研究过程中,以理论值与仿真值差值的平方和最小为目标函数,对19个设计变量进行分析,重要变量如表3所示。
5.2 试验设计(design of experiments)
试验设计考虑的是多个设计变量同时变化对样机性能的影响。试验设计结果如下:
(1)以零级角度理论值与仿真值差值的平方和最小为目标,部分较好结果见表4。从表中可看出,第8次试验的结果更好。
(2)以一级角度理论值与仿真值差值的平方和最小为目标,部分较好结果见表5。可见,第20次试验的结果更好,但参数DV_3与表4中计算结果矛盾。
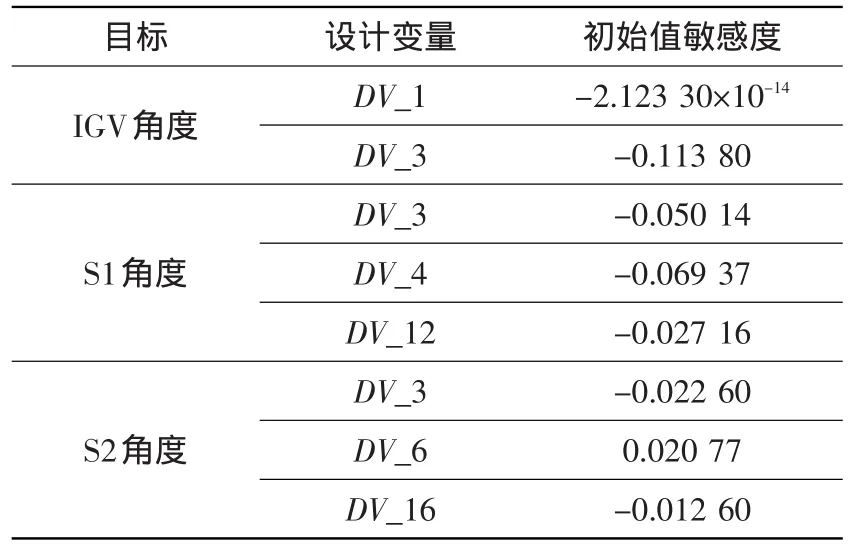
表3 设计研究结果Table 3 Results of design study
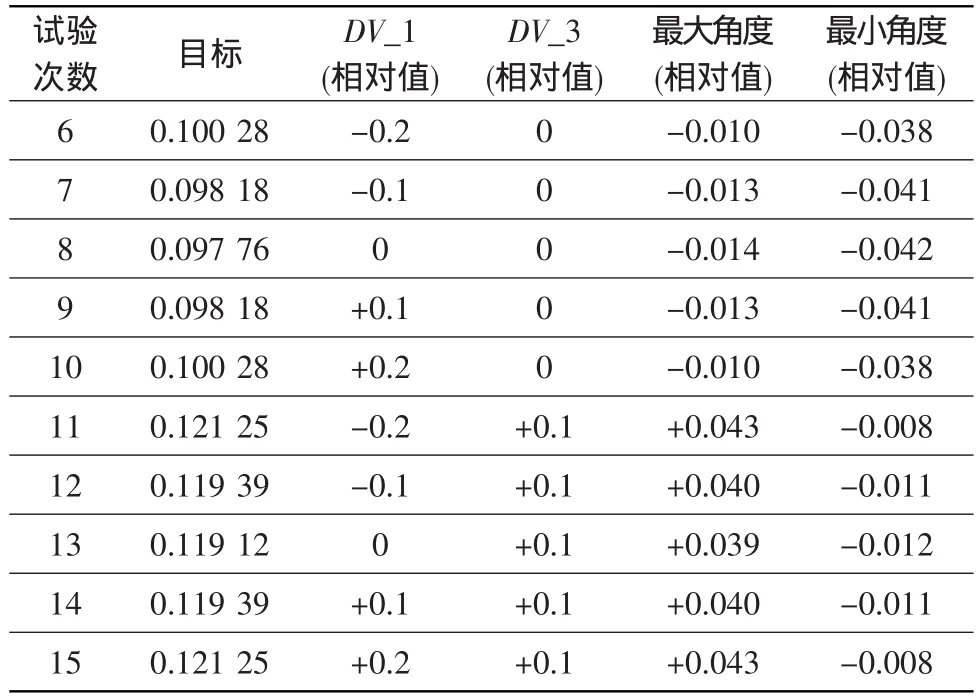
表4 IGV角度试验设计结果Table 4 Results of design of experiments on IGV angles
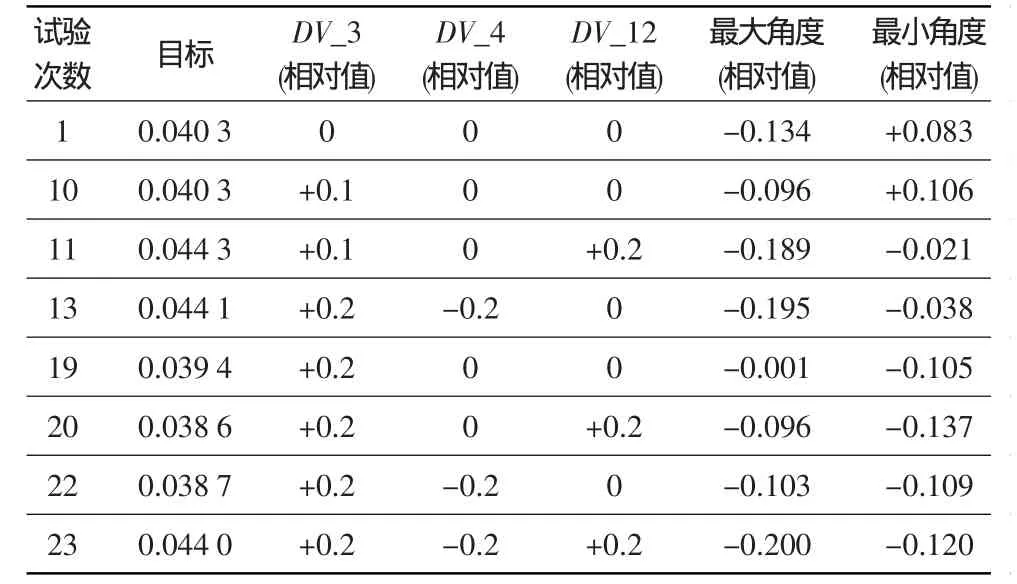
表5 S1角度试验设计结果Table 5 Results of design of experiments on S1 angles
(3)以二级角度理论值与仿真值差值的平方和最小为目标,部分较好结果见表6。可见,第22次试验的结果更好,参数DV_3与表5中计算结果一致。
5.3 优化分析
优化分析可归结为:在满足各种设计条件和指定变量变化范围内,通过自动选择设计变量,由分析程序求取目标函数的最大值或最小值。优化分析与试验设计各有优点,互为补充。试验设计除了可获得正确的分析结果外,还能研究参数间的关系和影响[6];而优化分析着眼于获得最佳目标值。优化分析结果如下:
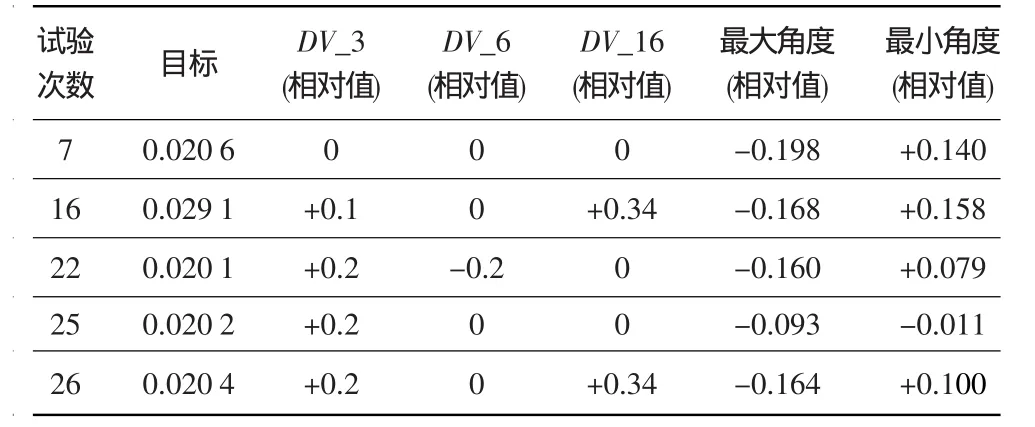
表6 S2角度试验设计结果Table 6 Results of design of experiments on S2 angles
(1)以零级角度理论值与仿真值差值的平方和最小为目标,分析结果如表7所示。从表中可看出,初始值对于零级静叶的调节角度为最佳设计。
(2)以一级角度理论值与仿真值差值的平方和最小为目标,分析结果如表8所示。
(3)以二级角度理论值与仿真值差值的平方和最小为目标,分析结果如表9所示。
以上分析仅考虑了运动学范畴。从试验设计和优化分析结果看,DV_3对各级角度的影响较大,且趋势不同。因此,还需综合考虑并进一步折衷。
(4)在动力学仿真模型中,以活塞受力最小为目标,以各级角度理论值与仿真值差值的平方和最小为约束条件(分别以C1、C2、C3表示),优化分析结果如表10所示。
从上面分析看,不同的试验设计会使得有些参数取值产生矛盾,且优化目标不同时参数取值也会发生冲突。因此,有些参数需要折衷。
6 仿真结果分析
将ADAMS参数化的简易模型与文献[5]中的调节机构虚拟样机模型进行仿真对比分析。
6.1 运动学仿真对比分析
在两种模型的活塞杆上添加样条函数驱动以模拟活塞行程。仿真的角度变化规律、活塞行程如图3及表11所示。从图、表中可看出,两个模型的角度有微小差异,但活塞行程差距较大。虚拟样机零件数多且较复杂,其仿真结果可认为更接近于实际机构的运动情况。但在方案设计阶段,简易模型的角度结果也可接受,只是活塞行程要在后续详细设计中加以修正。
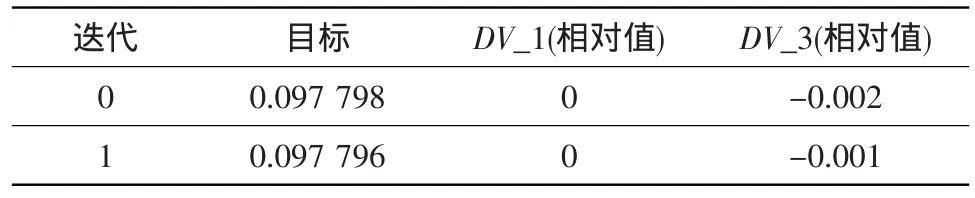
表7 IGV角度优化分析结果Table 7 Results of optimization on IGV angles
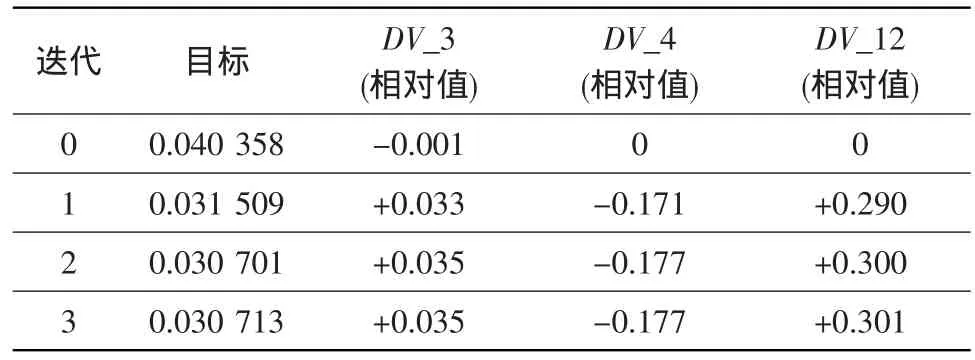
表8 S1角度优化分析结果Table 8 Results of optimization on S1 angles
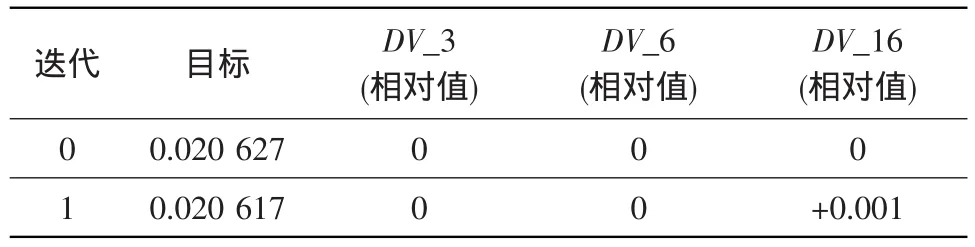
表9 S2角度优化分析结果Table 9 Results of optimization on S2 angles
6.2 动力学仿真对比分析
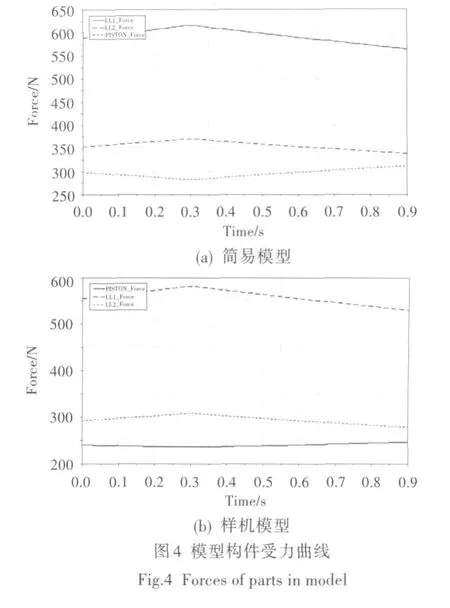
在活塞上添加不同的样条线驱动力函数,以保证两种模型的调节角度变化符合设计规律。仿真时主要关注活塞杆及两根连动杆的受力变化情况,主要关注活塞杆及两根连动杆的受力变化情况,结果如图4及表12所示。叶片上输入的力矩为气动估算结果,仿真精度不高,但可通过动力学模型研究各构件的受力情况(主要是变化趋势)。从图、表中可看出,两种模型各构件的受力值较接近。在机构方案设计阶段,简易模型可用于动力学初步分析。

表10 优化分析结果Table 10 Results of optimization
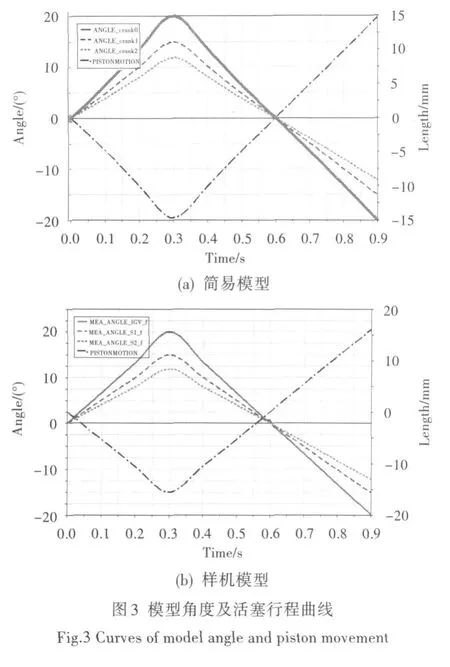
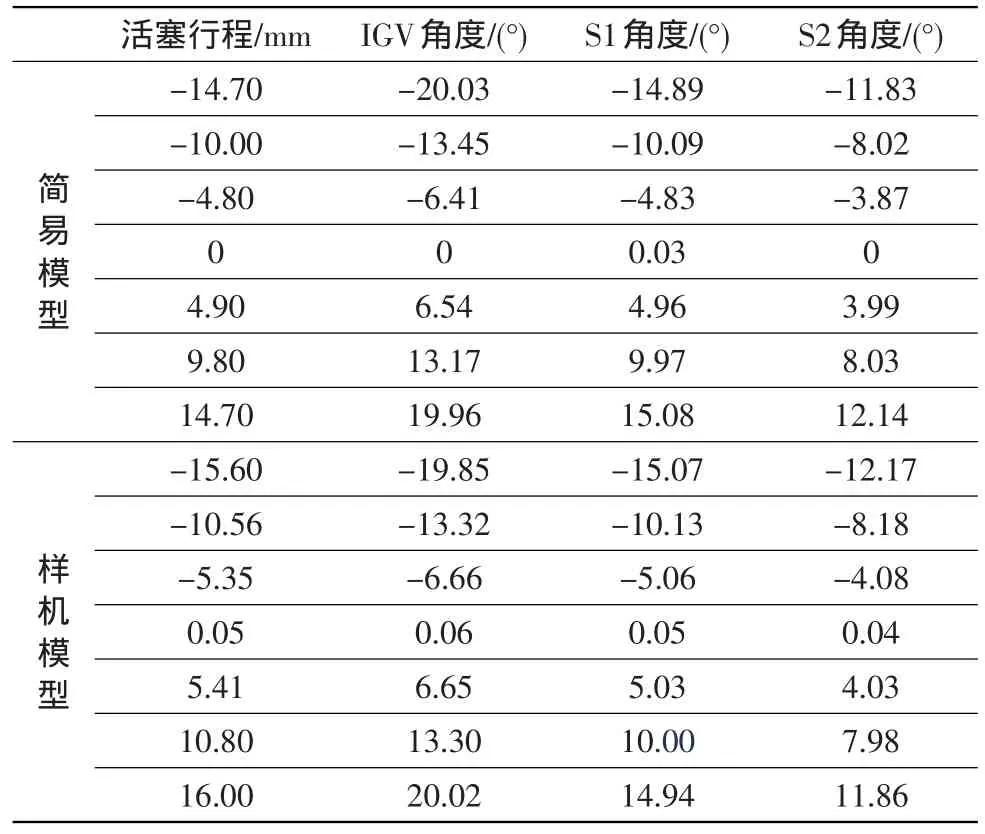
表11 运动学仿真对比结果Table 11 Comparison of simulation results on kinematics
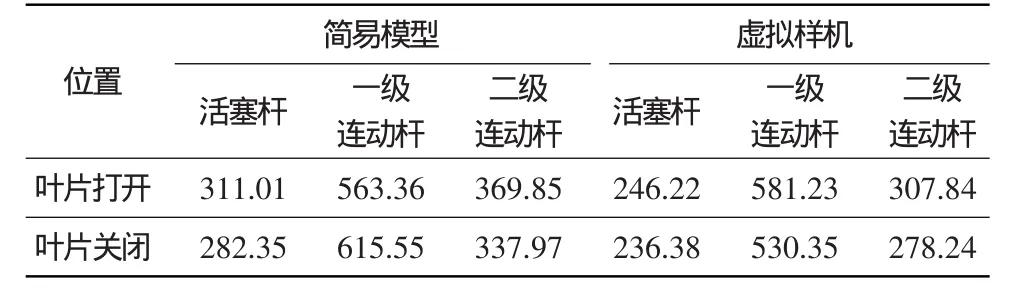
表12 构件受力对比结果 NTable 12 Comparison of forces on parts
7 结论
(1)在调节机构方案设计中,可使用ADAMS建立简易机构参数化模型,其运动/动力学仿真结果满足设计要求。
(2)使用参数化分析方法建立的调节机构简易模型,通过设计研究可确定影响调节角度的重要参数,并对这些参数进行试验设计和优化分析,可快速有效地得出较优的机构设计结果。
[1]舒士甄,朱 力,柯玄龄,等.叶轮机械原理[M].北京:清华大学出版社,1991.
[2]The Jet Engine[M].5th ed.ROLLS-ROYCE plc,1996.
[3]高效节能发动机文集编委会.高效节能发动机文集:第3册——风扇、压气机设计与试验[M].北京:航空工业出版社,1991.
[4]航空发动机手册编辑部.CFM56发动机手册汇编(第6册)[G].1983.
[5]杨 伟,罗秋生,张少平,等.基于UG和ADAMS的调节机构虚拟样机动力学仿真[J].燃气涡轮试验与研究,2009,22(2):22—26.
[6]陈立平,张云清,任卫群,等.机械系统动力学分析及ADAMS应用教程[M].北京:清华大学出版社,2005.
