基于遗传算法的发动机气路性能模型修正研究

李 冬，王冠超，曹明川

(1.海军航空工程学院研究生管理大队，山东烟台264001；2.海军驻长春地区航空军事代表室，吉林长春300000)

1 引言

通常根据发动机的额定特性来建立发动机的数学模型，忽略了不同发动机之间的性能差异和使用过程中的性能蜕化。因此，计算出的发动机性能参数与发动机实际性能参数存在较大误差[1]。加之发动机各部件特性为单独得到，而发动机作为一个整体共同工作，即使所得各部件特性十分精确，但各部件间的相互影响和一些随机因素的干扰，使得各截面的特性参数及发动机输出的性能参数也不尽相同，因此有必要对模型进行修正。发动机稳态模型的修正过程在一定程度上即为模型参数的优化过程。遗传算法(GA)作为一种新的智能算法，采用人工进化的方式对目标空间进行随机搜索[2]，在参数寻优方面有其独特优势。基于此，本文采用遗传算法作为模型修正算法。利用相关性分析确定部件修正参数(发动机部件特性参数)和目标性能参数(发动机整机性能表征参数)作为模型修正基础，在求解发动机稳态性能模型六个平衡方程的基础上[3]，构造发动机性能模型修正代价函数，完成对发动机稳态模型的修正；计算了几种不同工况的发动机修正前后的特性参数，并将修正后的特性参数与用影响系数矩阵方法[4]所得修正结果进行对比；进一步讨论了利用不同部件修正参数组合修正发动机稳态模型。

2 发动机性能模型修正代价函数的构建

在发动机稳态模型基础上，用误差向量E={εi,i=1,…,6}构造代价函数，用ai表示大于零的权系数，构造求解发动机稳态模型的代价函数[5，6]：

当模型计算输出值与设计值误差较大时，引入部件修正因子(定义为k=Ve/Vm，其中Vm、Ve分别为发动机各部件的设计参数值和修正后的参数值)。

发动机稳态模型修正思路为，通过选择合适的k，将发动机性能计算模型中的Vm用kVm替代，而使模型计算值与发动机设计参数值相一致。则式(1)可进一步描述为：

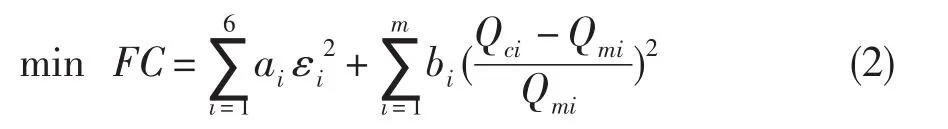
式中：F C表示预测性能参数值和设计性能参数值的差异，bi为大于零的权系数，Qmi为发动机设计第i个参数值，Qci为相应发动机模型第i个计算结果。式(2)也可表示成求解发动机稳态模型初始变量xi和修正因子kl的函数[7]：

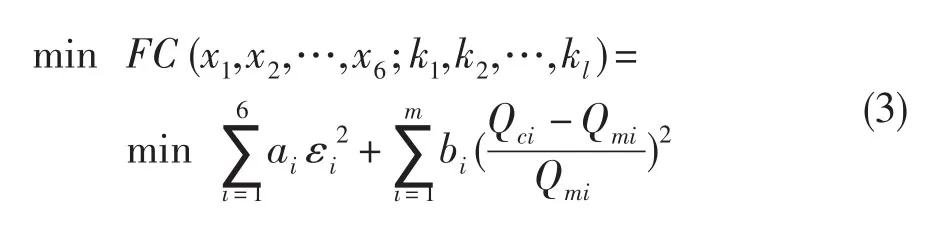
式中：l为修正因子向量维数，m为发动机参数设计值与模型计算值误差向量维数。

值得注意的是，很多时候l和m并不相等。并且在式(3)满足最小值要求下，l＞m时kl(1,2,…,l)存在无穷个解；l≤m时kl(1,2,…,l)存在唯一的最小二乘解，且只有l=m时式(3)的最小值为0，其它情况则不然[8]。为提高模型修正精度，本文只考虑l=m的情况。

3 性能模型修正因子的优化选择

3.1 修正因子选择原则[9]

恰当选择部件修正参数对自适应模型求解十分重要。在选择待修正的部件参数时，需考虑以下几个重要因素：

(1)所选择的部件修正参数必须与目标性能参数有很强的关系，否则在自适应修正过程中没有足够的搜索空间，不能搜索到更优的修正结果。

(2)部件修正参数个数没有限制，但修正参数选择不同会导致修正效果不同；部件修正参数个数选择越多，搜索空间越大，所获得的修正结果就越接近目标参数。

(3)部件修正参数的上下限同样决定了搜索空间范围，因此在自适应修正过程中，选择参数合适的上下限十分重要，这可能需要多次试验来确保最优值包含在搜索空间中。

3.2 优选性能模型修正因子

就发动机安装工艺而言，风扇、压气机、涡轮叶片的制造公差和装配工艺偏差是造成单台发动机试车参数不一致的主要因素，从而导致风扇、压气机和涡轮等核心机部件的特性线产生差异。根据上述分析，确定风扇流量Wa22、风扇效率ηcL、风扇增压比πcL、高压压气机流量W3、高压压气机效率ηcH、高压压气机增压比πcH、高压涡轮流量Wst45、高压涡轮效率ηTH、低压涡轮流量Ws t5和低压涡轮效率ηTL作为发动机部件修正参数选择对象。考虑到实际情况与参数测量难易，确定目标性能参数为高压压气机出口压力P3、低压涡轮出口温度T5、尾喷口出口温度T8、发动机推力F和耗油率sfc。

发动机某个部件特性参数变化，可能对发动机某些截面测量参数输出量影响较大，而对另一些输出量影响较小；而某个截面参数输出量变化，可能由若干部件特性参数的变化引起。利用相关性分析方法，找出部件修正参数的最佳组合作为发动机模型修正基础。这里定义相关系数为：

在相关性分析前，首先求出发动机部件修正参数与目标性能参数间的相关系数。基于此，本文利用单个部件修正参数扰动法，即依次将部件修正参数减少2%，同时保持其余部件修正参数不变，计算发动机特性参数。其结果见表1。

由于相关性分析的目的是找出对每个目标性能参数影响最大的部件修正参数。为便于分析，应对相关系数进行归一化处理。按列进行归一化处理，归一化相关系数计算式为：

归一化后的相关系数见表2。其中，相关系数大于0.5可认为是强相关，在0.3～0.5之间为中等相关，小于0.3的为弱相关。由此可看出，表中相关程度基本为弱相关，但具体数值不同。针对此情况，继续构造参数优选指标(敏感系数)：

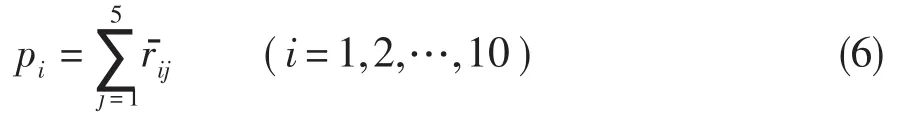
表1 部件修正参数减少2%后目标性能参数的变化 %Table 1 Variation of objective performance parameters when decreasing 2%of each component modified parameter

表2 归一化后的相关系数表 %Table 2 Related coefficients after normalization

图1示出不同部件修正参数的敏感系数。同时，为比较分析不同参数组合对稳态模型的修正结果，选取有代表性的三组数据：第一组敏感系数排在前五的部件修正参数，即Wa22、ηcL、πcH、Wst45、Wst5；第二组排在后五的部件修正参数，即 πcL、W3、ηcH、ηTH、ηTL；第三组为排在中间的五个部件修正参数，即Wst45、Wst5、πcL、W3、ηcH。此时，选取的部件修正参数与目标性能参数数目一致，故kl(1,2,…,l)有唯一解。

4 基于遗传算法的发动机模型修正

遗传算法的算法流程如图2所示，基于遗传算法的发动机稳态模型修正过程如图3所示。在一定的环境和控制条件下，用该点的发动机部件参数x和k带入发动机稳态模型进行仿真，所得发动机性能参数与该点发动机设计参数值相比较。

当发动机设计参数值被作为目标性能参数时，任何适当的部件修正参数和修正因子均可用代价函数来估计其模型修正能力的好坏，目标函数定义为。式(2)中，ai(i=1,2,…,6)和bj(j=1,2,…,m)是考虑不确定因素及目标性能参数的相对重要性权值。在此，假定所有目标性能参数的权重都相等，即：

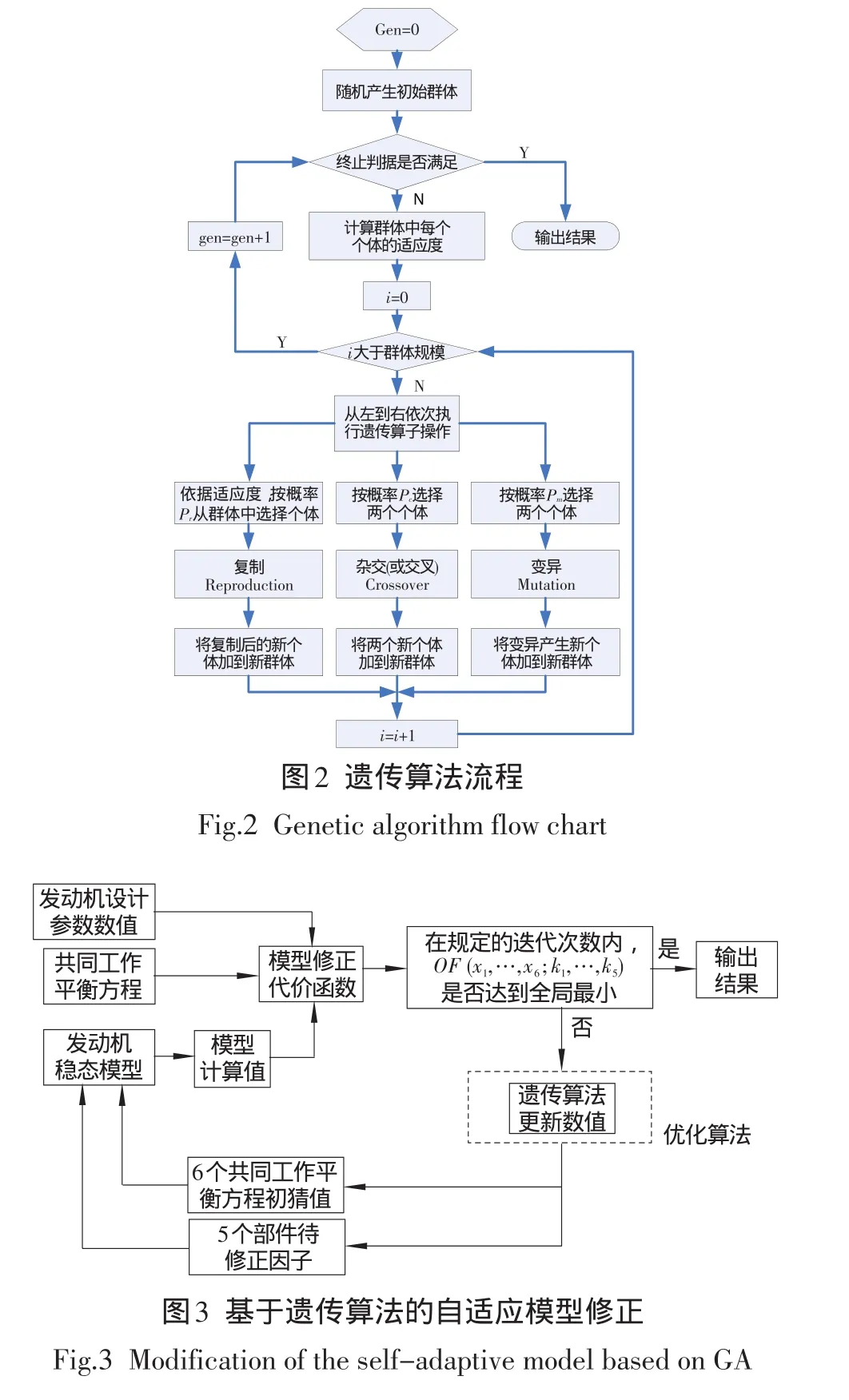
式中：适应度函数在0～1之间变化，1表示最优，0表示最差。

5 仿真结果与分析

5.1 修正前的稳态模型计算结果

以发动机某状态为例(设为工况1，Ma=0、H=0)，计算得到发动机模型修正前的目标性能参数，并与设计参数值进行比较分析，结果见表3。可见，修正前T5、T8、F与设计值偏差很大。如用此模型进一步分析发动机性能会产生较大误差，因此有必要对发动机模型进行修正。

表3 模型修正前的目标性能参数偏差Table 3 Deviation of objective performance parameter before model modification

5.2 修正后的稳态模型计算结果

采用前文的遗传算法参数优化流程修正发动机稳态模型。经反复试验，最终确定交叉率为0.7，变异率为0.05，种群规模为40，在设计值附近随机产生初始种群，最大迭代次数为100。修正后的结果见表4。对比表3和表4可知，经遗传算法修正后，发动机性能模型精度得到提高。

目标性能参数P3 T5 T8 F s f c与设计值的相对偏差/%-0.392 0 0.692 9 0.261 6 1.889 5-1.233 9

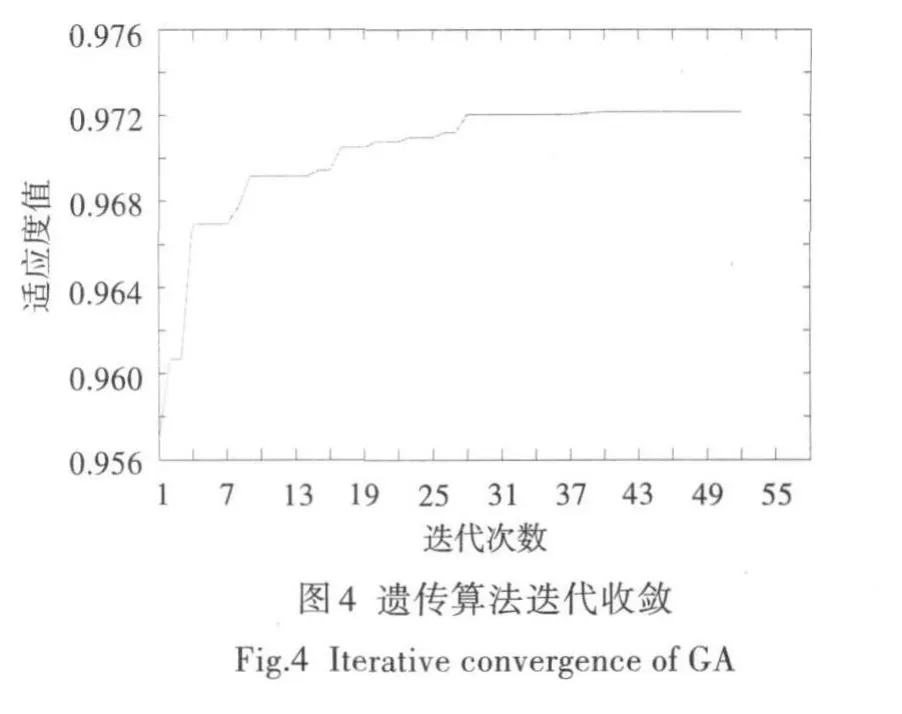
图4示出了遗传算法适应度值的变化过程。可见，经过52次迭代，遗传算法适应度值很快到达0.972，说明模型修正收敛速度较快。

5.3 与影响系数矩阵方法修正结果的对比

利用影响系数矩阵方法[4]对发动机稳态模型进行修正。首先进行一次修正，得到一次修正矩阵：

一次修正后的目标性能参数偏差如表5所示。对比表3和表5可知，修正后T5、T8、F的精度提高，P3、sfc的精度降低。个别参数偏差仍然过大，有必要进行多次修正。

表5 一次修正后的目标性能参数偏差Table 5 Deviation of objective performance parameter after primary modification

进一步修正，得到多次修正矩阵为：

表6为经多次修正后的目标性能参数偏差。对比表5和表6可知，多次修正后，目标性能参数与设计值的相对偏差减小，但精度低于遗传算法修正结果。因此，单从精度方面讲，遗传算法修正精度优于多次修正的影响系数矩阵方法。

表6 多次修正后的目标性能参数偏差Table 6 Deviation of objective performance parameter after multiple modifications

5.4 不同部件修正参数组合的模型修正结果

基于遗传算法，分别采用第二组和第三组部件修正参数进行修正。与设计值的相对偏差结果见表7。对比表7和表4发现，敏感程度最高的一组参数得到的模型修正效果最好。由此得到，正确选择合适的修正参数，对模型修正效果起关键作用。

表7 不同部件修正参数组合的目标性能参数偏差Table 7 Deviation of objective performance parameter of various components

5.5 不同工况的模型修正结果

利用最敏感一组参数对发动机稳态模型进行修正，另选取两个工况(都为加力状态，分别记为工况2和工况3)，验证此组参数对模型修正的泛化能力。模型修正误差结果如图5所示。分析图中可知，该组参数对模型修正具有较强的泛化能力，两个工况的修正精度基本满足要求。

6 结论

(1)采用遗传算法对发动机性能模型进行修正，其模型精度较修正前有很大提高，取得了不错的修正效果。

(2)单从修正方面讲，基于遗传算法得到的修正效果比影响系数矩阵方法得到的修正效果更好。

(3)对不同部件修正参数组合的模型修正，选取的部件修正参数越敏感，模型修正的效果越好。

(4)利用相关性分析选取发动机部件修正参数修正不同工况的发动机性能模型，可取得较好效果。

[1]翟高兰.航空发动机非线性参数估计方法[D].南京：南京航空航天大学，2008.

[2]苏三买.遗传算法及其在航空发动机非线性数学模型中的应用研究[D].西安：西北工业大学，2002.

[3]尹大伟.航空发动机模型求解算法及性能寻优控制中的参数估计研究[D].长沙：国防科技大学，2011.

[4]Escher P C，Singh R.An Objective-Oriented Diagnostics Computer Program Suitable for Industrial Gas Turbine[C]//.21stInternational Congress on Combustion Engines.Switzerland，1995.

[5]尹大伟，李本威.某型涡扇发动机模型修正研究[C]//.中国航空学会第六届动力年会.2006.

[6]李本威，尹大伟，王永华，等.某型涡扇发动机状态模型修正[J].海军航空工程学院学报，2008，23(2)：213—216.

[7]付尧明，傅 强.非线性航空发动机性能参数估计方法研究[J].机械设计与制造，2006，(8)：140—141.

[8]Mathioudakis K，Kamboukos Ph，Stamatis A.Turbofan Performance Deterioration Tracking Using Nonlinear Models and Optimization Technique[J].Journal of Turbomachinery，2002，124(10)：580—587.

[9]谢小平.基于单机修正的某型发动机气路模型的建立研究[D].山东烟台：海军航空工程学院，2011.