航空发动机转速摆动问题研究

姚华廷，徐 敏，王 曦

(1.北京航空航天大学，北京100191；2.空军装备研究院总体所，北京100085；3.中航工业黎阳公司，贵州平坝561102)

1 引言

第二代航空发动机液压机械控制器，采用保持低压转子转速n1、喷口面积及涡轮膨胀比不变(加力状态)，并限制高压转子最大转速的控制规律。当确定发动机工作状态的油门位置不变时，通过主燃油泵的等压差活门开环供油调节n1(n1＜85%)和离心式转速调节器闭环调节(n1≥85%)保持n1不变。其转速调节品质可通过n1的摆动量来衡量[1]。当油门手柄位置一定时，允许的转速摆动量为：n1＜88%时不超过±0.5%，n1≥88%时不超过±0.3%。使用中，转速摆动量超过上述规定范围时，不仅会造成发动机和飞机的强烈振动，损坏机件，而且在空中还会给飞行员的操纵带来困难，危及飞行安全[2，3]。导致发动机转速摆动的原因很多，但通常把由发动机调节系统引起的摆动称为真摆动，由指示系统造成的摆动称为假摆动。真摆动属于控制品质问题，是本文的主要研究方向。

转速摆动问题一直受到工程人员和科研人员的重视，并做了大量研究工作。工程人员从密封、工艺、磨损和结构等方面做了大量改进，并取得一定成效。科研人员对控制器建立了控制系统的线性数学模型，并进行了稳定性分析和仿真计算，探索了分油活门重叠量、给定弹簧刚度及预压缩量、离心飞重重量和反馈活门重叠量等因素对发动机控制系统性能(特别是稳定性)的影响[4～7]。但这些分析和仿真存在一些不足，对转速控制器结构的分析不够充分和准确，没有找到摆动故障的原因。

为此，本文针对某型航空发动机转速摆动问题，对控制器的比例积分控制原理进行了分析，采用AMESim建立液压机械式转速控制器燃油调节器的模型，对控制器原理进行了仿真；详细分析了转速摆动机理并通过试验进行了验证，给出了转速摆动问题的解决思路。

2 闭环转速控制器模型

闭环转速控制器模型由机械离心飞重、带衬套分油活门、带反馈杠杆的反馈活塞、反向活门、中腔层板和随动活塞组成[8]，如图1所示。当调节器处于平衡位置时，反馈活塞的反向活门处于中立位置，即反向活门处于关闭中腔进油路和出油路的位置，是一个闭死区间。与反馈杠杆相连接的分油活门衬套和分油活门也处于中立位置，且带衬套分油活门的中立位置由反向活门的中立位置闭死区间决定，闭死区间越大，带衬套分油活门的中立位置区间也越大，相应的调节误差就越大，系统的灵敏度变差，但稳定性变好。作用在分油活门右端的换算离心力与左端的调准弹簧力相等，分油活门稳定在中立位置附近，通往随动活塞左腔的开度与通往反馈活塞右腔的开度基本相等，作用在随动活塞左腔的油压力和斜盘反力与作用在反馈活塞右腔的油压力和弹簧力平衡[8，9]。

由此可知，当分油活门处于中立位置时，转速偏差为零。当转速指令(即弹簧力)或实际转速(即离心飞重离心力)变化时，分油活门偏离中立位置，产生转速偏差e，分油活门通往左、右腔的开度变化，流入左、右腔的流量变化，反馈活塞和随动活塞移动到一新的位置(流量到位移为一积分环节)。同时，随动活塞通过反馈杠杆带动分油活门衬套移动，使分油活门两边开度重新达到平衡。从偏差e到反馈活塞新位置为一惯性环节，稳定时反馈活塞新位置与e成比例，实现比例控制，但反馈活塞的运动限制了最大比例控制的输出值。同时，反向活门根据相应偏差，打开进油孔和回油孔，改变流入或流出中腔的流量，使中腔长度发生变化(流量到中间长度为积分环节)，从而控制随动活塞位置，实现积分控制，但最大积分系数受中腔层板限制。所以闭环转速控制器是一个带比例积分最大值限制的比例积分控制器，其控制框图见图2。

通过以上分析可看出，为提高系统稳定性，控制器设计时采取了以下几项措施：①比例控制器由带比例反馈的液压放大器实现；②转速指令值大于实际转速时，限制比例控制器中的最大控制量，同时使用层板限制器限制最大积分控制输出值；③限制积分控制器的最大控制量，且偏差较小时利用反向活门正重叠关闭积分控制器。

相反，为提高系统准确性和灵敏度，也采取了一些措施：①采用较小的反向活门正重叠量，减小中立位置闭死区间；②增大反馈杠杆传动比值，减小分油油门中立位置闭死区间；③分油活门采用负重叠，保证稳态时正常液压油流动；④用反馈活塞右腔弹簧力平衡柱塞泵斜盘反力。

采用AMESim建模，第一个难点是确定分油活门的中立位置，第二个难点是确定反馈活门的最大位移限制(即比例值的饱和限制)。根据以上分析，建立如图3所示模型。

3 控制器原理仿真

模型调试按以上分析进行。进行开环调试，给定一转速偏差e，当e在中立位置范围内时，反馈活塞的反向活门处于中立位置，层板节流器处于关闭状态；当e较大时，反馈活塞位移与e成比例，层板节流器处于打开状态，反馈活塞匀速运动。

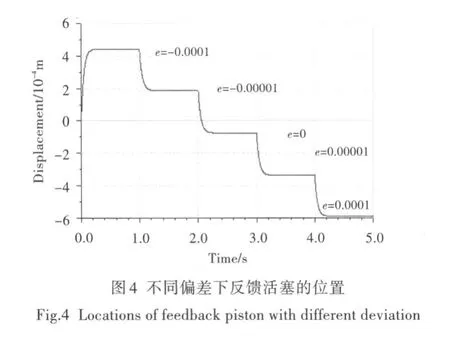
图4为不同偏差输入时反馈活塞的位置变化曲线。输入偏差为0时，反向活门处于中立位置，中腔与定压油和低压腔均未沟通。在不同偏差作用下，反馈活塞很快达到平衡位置，惯性环节时间常数很短，且平衡位置与偏差成比例，起到比例环节作用。

图2 闭环稳态转速控制器控制框图Fig.2 Block diagram of closed-loop steady-state speed controller

从图5中不同偏差下反馈活塞与随动活塞的位移看，1.0～2.0 s时，实际转速比指令转速偏大，且偏差较大时，反馈活塞位移量与误差成正比，偏差不变，反馈活塞位移不变，反向活门通低压腔，随动活塞在积分控制作用下向右移动。2.0～3.0 s时，实际转速比指令转速偏小，反馈活塞位移量与偏差成正比，偏差不变，反馈活塞位移不变，且误差较大时反向活门通低压油，随动活塞在积分控制作用下向左移动。另外，中腔层板流量不影响反馈活塞运动，只会作用于随动活塞，反馈活塞位移只与偏差有关，积分作用大小不影响比例反馈，保证比例控制正常工作。图6示出了不同偏差下各腔压力变化。可见，中腔压力由左腔和右腔中压力较低的腔压决定，保证了积分控制器的正常工作。

上述仿真和分析说明，闭环转速控制器为一个比例积分控制器，反馈活塞的位移输出进行比例控制，反向活门的流量进行积分控制。

4 转速摆动机理分析

假设发动机模型为一阶惯性环节，将图2中的稳态转速控制器和发动机模型闭环起来，如图7所示。

图6 不同偏差下前、中、后腔压力变化Fig.6 Pressure of left,middle and right chamber with different deviation

图7 闭环转速控制器与发动机闭环模型Fig.7 Block diagram of controller and engine

从图中可得系统的传递函数：

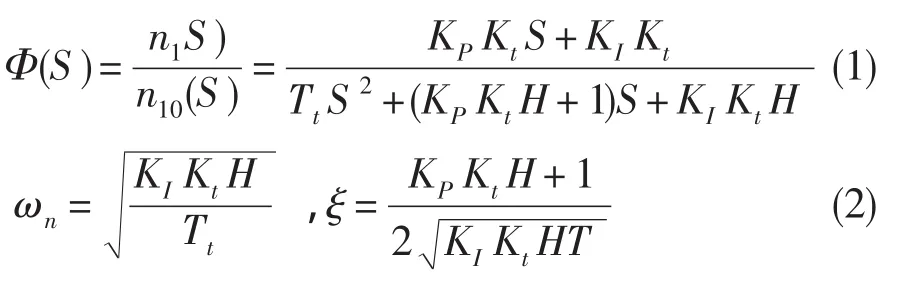
特征方程特征根的实部为-(KPKtH+1)/2Tt，系统稳定。增大比例控制量，特征根实部远离虚轴，稳定性变好；增大比例控制系数KP，减小积分系数KI，阻尼系数ξ增大，抗干扰能力增强。但在工程实践中，除减小中腔层板流量来减小KI外，常通过减小控制量来解决或减小转速摆动，如通过减小分油活门凸边倒角、减小分油活门直径等来减小比例控制量，反而降低了系统的稳定性。所以从提高稳定性和抗干扰能力的方向考虑解决转速摆动稳定性的思路行不通，需另行考虑。

4.1 开环频率特性仿真与分析

在仿真分析转速摆动过程中，从发动机输出端加入各种频率的转速脉动信号，但观察信号经转速控制器后反馈活塞端输出时，高频信号几乎被滤掉，低频信号也被衰减。由前文可知，比例控制器由带比例反馈的液压放大器实现，若忽略惯性力，带比例反馈的液压放大器为一惯性环节，具有低通特性；如果交接频率变高，某些频率段的摆动没有有效衰减，很可能造成转速摆动。考虑惯性力，反馈活塞和分油活门套筒是典型的质量弹簧系统，带比例反馈的液压放大器会表现出二阶振荡环节特性，当阻尼系数小于某值时，幅频特性会出现谐振峰值，谐振频率附近的扰动信号会被放大，也会引起转速摆动。为此，对带比例反馈的液压放大器进行频率响应仿真就十分必要。频率响应仿真模型如图8所示，输入为分油活门位移，给定一定频率的正弦信号，输出为反馈活塞位移。

根据图8中模型，分别输入频率从0.1 Hz到2.4 Hz，间隔频率0.1 Hz，幅值0.3 mm的分油活门位移偏差信号，输出的反馈活塞位移幅值如表1所示。

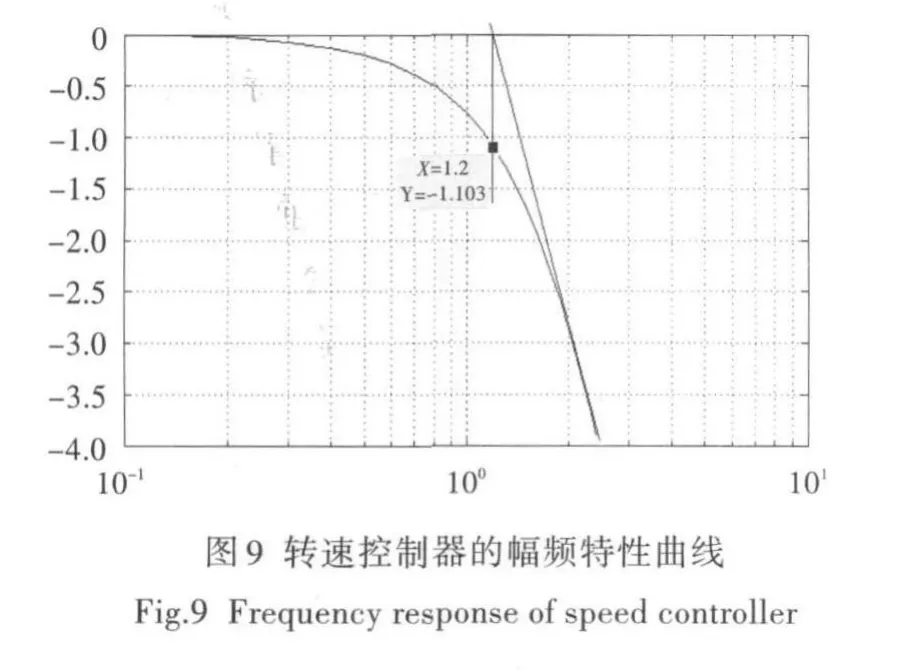
按表1数据绘制的转速控制器的幅频特性曲线如图9所示。通过仿真得到的交接频率范围约为0.8～1.2 Hz。发动机的自然频率0.4～0.5 Hz，有效信号能顺利通过液压放大器，这也验证了用惯性环节实现比例伺服控制的低通滤波作用。

分析发生过的转速摆动数据，一般是低频摆动，周期集中在0.5～1.5 s之间(相应频率0.66～2.00 Hz)，在1.0 s最为集中。而液压伺服比例控制器交接频率约0.8～1.2 Hz，转速摆动频率分布在其两端。研究这两者的关系对于找到转速摆动原因意义重大。

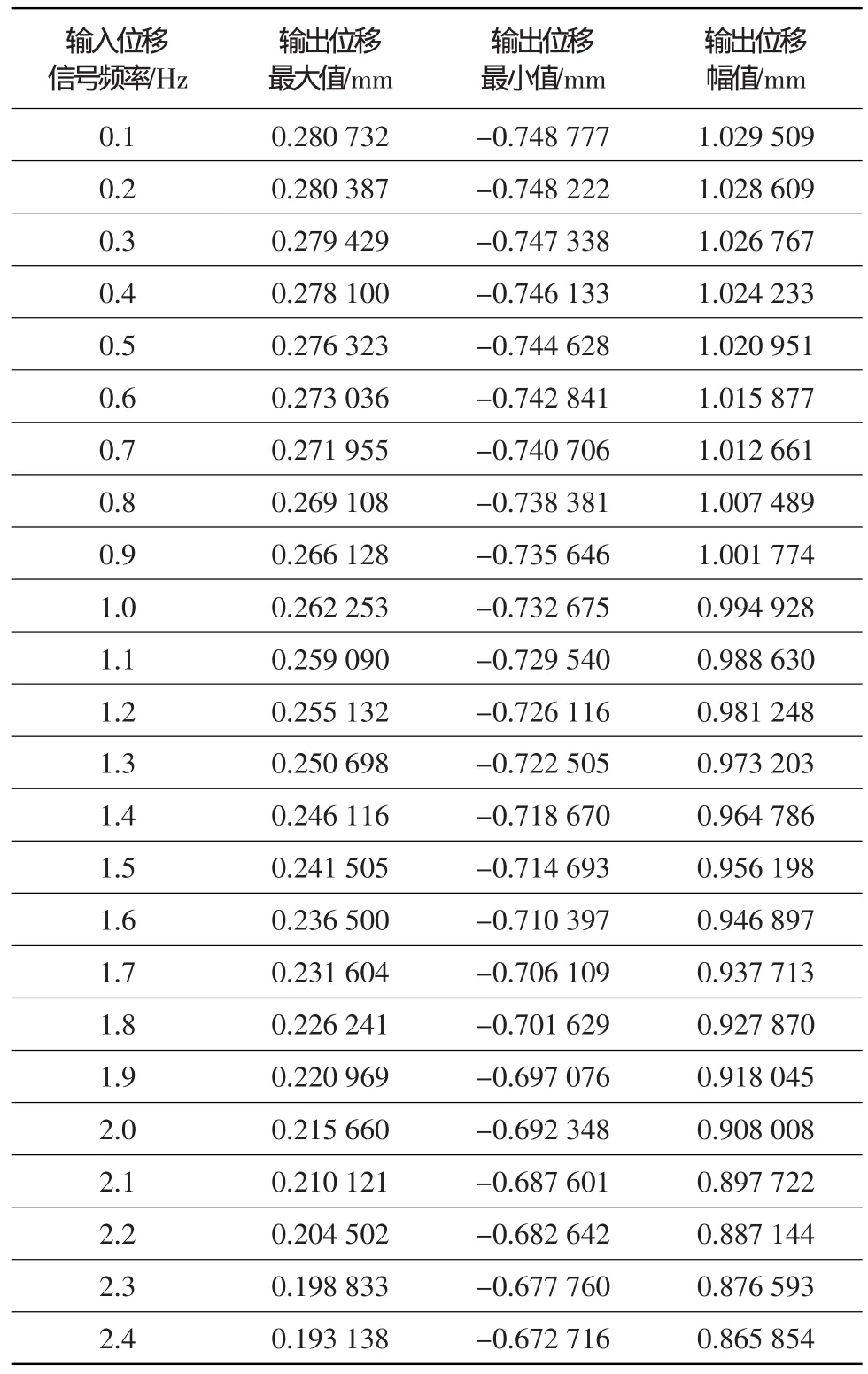
表1 频率响应仿真数据Table 1 Data of frequency response simulation

在平衡点附近加入偏置幅值，在不同偏置幅值正弦信号作用下，液压伺服比例机构的频率特性曲线会发生变化。特别是当离中立平衡点偏置值越来越小时，原本表现出的典型一阶惯性环节的频率特性，会表现出二阶振荡欠阻尼时的频率特性，且一阶惯性环节的交接频率与二阶振荡环节的谐振频率基本相同。

假设转速控制器中实现比例控制作用的比例伺服阀的特性与文献[10]中的类似：平衡点转速偏置值大于±0.3%时，比例伺服阀的频率特性表现为一阶惯性环节；偏置值小于±0.3%时，频率特性表现为欠阻尼的二阶振荡环节，谐振频率约1.0 Hz左右。

按以上假设，当转速控制器与发动机组成闭环后，在1.0 Hz频率附近小于±0.3%的外界干扰信号会被放大，放大的干扰信号经过发动机后频率仍在1.0 Hz附近，再次通过离心飞重和伺服比例控制器放大，直至达到±0.3%。当外界干扰动信号大于±0.3%时，比例伺服阀会将其衰减，直至≤±0.3%。发动机转速摆动量就能控制到±0.3%。

如果比例伺服阀的频率特性表现为欠阻尼二阶振荡环节的平衡点偏置值大于±0.3%，如达到±0.5%，则转速控制系统的转速控制精度只能达到±0.5%，就会在谐振频率附近产生至少±0.5%的转速摆动量。同时，由于比例控制器的输出(即反馈活塞位移)直接决定反向活门的打开和关闭，摆动量大小会通过积分控制器进一步加强。由以上假设和分析可得出：转速摆动问题归根结底为伺服比例控制器的精度问题，转速摆动频率分布在伺服比例控制器交接频率附近(在1.0 Hz处最为集中)。分析结论与实际故障数据吻合，故障现象得到很强的理论解释。

按以上分析，发动机闭环转速控制器的控制精度可通过比例伺服阀的开环频率特性得到。频率仿真时，缓慢减小频率信号相对平衡点的偏离值，直至伺服比例控制器表现出欠阻尼的二阶振荡环节特性，这时的偏离值即为转速控制的精度值。

4.2 转速摆动分析试验验证

若单独对闭环转速控制器中的伺服比例控制器进行试验，输入信号为分油活门位移相对中立位置平衡点偏置的频率信号，测量反馈活塞对应的输出位移幅值将十分困难。且试验需单独研制相关设备和壳体组件，并保证单独试验的伺服比例控制器的工况与主燃油泵中的相同，调试伺服比例控制器分油活门至中立位置将十分繁杂且基本不具备工程可行性。因此，有必要找到一种工程可行的频率特性试验方法，最好能在主燃油泵里进行伺服比例控制器的频率特性试验。

主燃油泵在工厂产品试验台上进行整泵出厂试验中，闭环转速控制器调试时，输入信号是带动离心飞重转动电机的转速，观测的输出信号为油门开关后的油压。通过增加电机转速，观察油门开关后油压变化，调试油门杆角度对应的转速。电机的转速信号直接决定伺服比例控制器分油活门的位置。输出的油门开关后的油压也能间接反映反馈活塞位移。调试油门杆角度对应转速的过程中，通过微调可找到分油活门的中立平衡位置及中立平衡位置内偏上的位置。所以，通过输入一定幅值的正弦转速信号就能得到伺服比例控制器分油活门的偏离信号输入，通过观测油门开关后的油压可间接获取反馈活塞输出。

试验前，对转速电机电路做一定改造，在电机调整开关上并联一可调电阻分压器，用一PLC可编程控制器精确控制继电器通断，接通和关闭可调电阻分压器，模拟转速的正弦频率信号。试验步骤为：

(1)按试验转速大小调整转速扰动量幅值。通过手动开关调节电机至试验转速，接通继电器，调节可调电阻分压器阻值，使转速降低量满足试验要求。

(2)将油门杆置于自始转速以上某点(可事先设定，本文以3 500 r/min为例)。按调试大纲调试该油门杆角度对应的协同转速，调整到位后观察油门开关后的压力，压力降低后手动略微减小转速，使油门开关后的压力恒定。此时的位置对应平衡转速位置内偏上的位置。

(3)启动可编程控制器，输入频率分别为0.1 Hz、0.5 Hz、1.0 Hz、2.0 Hz、5.0 Hz、10.0 Hz的开关信号，接通和关闭可调电阻分压器，产生转速正弦频率信号。用数字示波记录仪记录油门开关后压力。

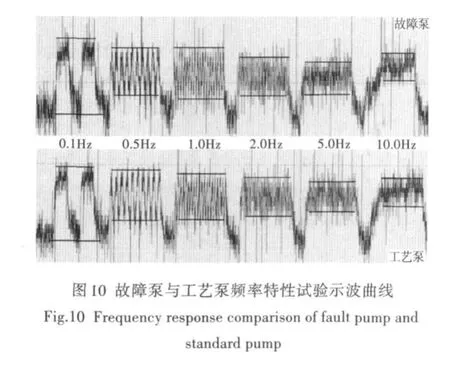
用两台泵做对比试验：一台为性能合格的工艺泵，另一台为故障泵(转速摆动范围0.8%，摆动频率约1～2 s)。在3 500 r/min试验转速下输入幅值为21 r/min的模拟正弦频率信号，观测结果如图10所示。可见，工艺泵频率特性表现出一阶惯性环节特性，能满足0.6%(即±0.3%)的精度要求；而故障泵在1.0 Hz频率处的输出幅值明显比0.5 Hz和2.0 Hz频率处的大，不满足±0.3%的精度要求，发生了转速摆动，摆动频率在1.0 Hz附近。

以上试验验证了前文对转速摆动原因分析的正确性。同时，这种开环频率特性的试验方法能检测主燃油泵的闭环转速控制精度，使用开环稳态试验台就能方便地发现转速摆动征兆，具有非常强的工程实用价值。

4.3 转速摆动问题的解决思路

解决转速摆动问题的思路可明确为三点：一是增大伺服比例控制器交接频率，使摆动频率表现为高频摆动；二是提高伺服比例控制器精度，这是解决转速摆动问题的“本”；三是在伺服比例控制器精度范围内，控制与反馈活塞一体的反向活门的闭死区间，减小积分环节开启对转速摆动量的影响，这是解决转速摆动问题的“标”。

增大伺服比例控制器交接频率的方法即减小惯性环节时间常数，可采用改进结构的方法实现。第三代发动机液压机械转速控制器中的比例控制器采用校正活塞实现，摆杆偏差通过液压力变化快速比例作用到校正活塞弹簧，惯性环节时间常数小，交接频率大，基本解决了转速低频摆动问题。

目前，工程中常用来提高分油活门式伺服机构精度的方法包括：提高分油活门和衬套的配合精度；提高凸台和窗口的锐边尖度；加强工艺管理防止锐边磨损。根据本文方法，可通过频率特性试验方法定量研究锐边尖度与伺服比例控制器精度间的关系。

另外，在保证控制稳态精度的前提下，适当加大反向活门的正重叠量，并提高凸台与窗口的锐边尖度，以此减小积分环节在摆动过程中的开启，加大对转速摆动量的影响。

5 结束语

本文建立了某型发动机闭环转速控制器的仿真模型，对闭环转速控制器的原理进行了分析和仿真验证。提出了该液压机械式闭环转速控制器采用了带比例积分最大值限制的比例积分控制器，分析了控制系统稳定性与结构参数间的关系，并否定了用提高控制系统稳定性的方法来解决转速摆动问题的思路。通过频率特性研究，发现转速控制器中伺服比例控制器的截止频率与转速摆动频率基本接近。根据比例伺服机构特性，分析得到转速摆动的根源是伺服比例控制器的精度，并能通过频率特性仿真方法得到。根据主燃油泵稳态调试台现有条件，结合现有调试方法，设计了主燃油泵频率特性试验。在同等输入下，对故障泵和工艺泵分别进行频率特性试验，有力地验证了转速摆动原因分析的正确性。该试验方法具有很强的工程实用性。

[1]樊思齐.航空发动机控制[M].西安：西北工业大学出版社，2008.

[2]Merovitch L.Elements of Vibration Analysis[M].New York：McGraw-Hill，1975.

[3]Rosenberg R C，Zou T.Power-Based Model Insight[C]//.Proceedings of the 1988 ASME Winter Annual Meeting,Symposium on Automated Modeling for Design.1988.

[4]高光良，樊 丁，戚学锋.航空发动机机械液压建模及仿真技术研究[J].计算机仿真，2006，23(1)：62—64.

[5]唐有才，王占勇，于德会，等.航空发动机转速摆动故障分析及预防措施[J].航空维修，2002，4：23—24.

[6]张睿智，曲东才.模糊推理在军用飞机转速摆动故障诊断中的应用研究[J].计算机测量与控制，2008，16(2)：153—155.

[7]田 巍.军用发动机转速摆动故障分析及预防措施研究初探[J].长沙航空职业技术学院学报，2007，7(2)：36—39.

[8]管彦深，张加桢.航空动力装置控制：系统部分[M].北京：国防工业出版社，1985.

[9]廉筱纯，吴 虎.航空发动机原理[M].西安：西北工业大学出版社，2005.

[10]Vickers.带反馈的比例方向控制阀[EB/OL].(2010-12-06).http://wenku.baidu.com/view/7793b56f58f afab069dc028b.html.