一种新的去强相关信号方法的波达方向研究

乐兵兵，吴多龙

（广东工业大学 物理与光电工程学院，广东 广州 510006）

DOA估计[1]是智能天线中非常重要的无线定位算法，且该算法也已广泛应用于雷达等目标定位领域。经典Music算法相比传统的DOA估计算法具有分辨率高，计算量小等优点。但是经典的Music算法不能分辨相干信号，因此探索一种适用于相干环境下的目标方位估计算法显的尤为重要。基于空间的平滑技术的改进的Music算法具有比较好的去相关性能，但是它是以牺牲天线的有效阵元数为条件了，而且它将天线接收阵分成了多个子阵，也一定程度上大大增加了计算量[2-4]，并且它对小信噪比信号和DOA相隔比较近的信号分辨率较低。文中利用TOPELITZ矩阵[5]多次重构输入协方差矩阵，再与经典的Music算法相结合，得到一种新的去相关信号的DOA估计方法，该方法能有效解决信号强相关问题。

1 信号基本模型

Music算法是基于对阵列输出信号协方差进行特征分解来估计DOA[6]的。将Rx分解为D个较大的和M-D个较小的特征值，D个较大的特征值对应的特征向量生成一个信号子空间，M-D个较小的特征值对应生成噪声子空间，基于信号子空间和噪声子空间正交的特性，决定信号零点，即信号DOA。设有D个信号源入射到M个天线阵列上，则接收的信号为：

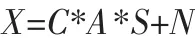
对X（t）的相关矩阵R进行特征值分解：

其中M=diag[λ0，λ1， …λM-1]，λ0≥λ1≥…λM-1为特征值，diag表示对角阵，V=[q0，q1，…qM-1]是R相应的特征向量，定义信号子空间为a（θ）={α（θ0），α（θ1），…α（θD）}，噪声子空间Vn=[qD，qD+1，…，qM-1]，则a（θ）与Vn正交，定义 Music 空间谱为：

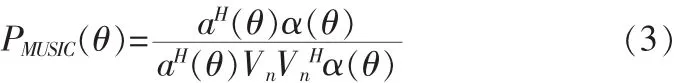
则通过谱峰搜索便可求出DOA。

2 改进Music算法的基本原理

若D个信号源中有某些信号源是相关或完全相关 （相干）的，则相干的几个信号就可能合并成一个信号，于是到达阵列的独立信号源数目将减少，即阵列输出信号协方差的秩Rank（RX）＜D，对信号协方差矩阵进行特征值分解后，得到的较大的特征值个数将小于D，而特征值为σ2的个数将大于M-D。与此相对应的信号子空间的向量也小于D，即特征向量生成的信号子空间的维数小于A={α（θ0），α（θ1），…α（θD）}的列数。 对某些相干源的方向矢量 α（θi）（i=1，…，D）将不再正交于噪声子空间，因而不出现信号零点，所以，有些信号源在空间谱曲线中将不呈现峰值，造成谱估计的漏报。

因此，要对Music算法进行改进，就是对阵列输出信号协方差矩阵进行处理，使信号协方差的秩恢复为Rank（RX）=D，从而能有效地估计出信号的DOA。

尽管对于相干信号源的情况已经有了空间平滑法，但它是以牺牲天线的有效阵元数（阵列孔径）为条件的，同时也增加了计算量，而且它对小信噪比信号和DOA相隔比较近的信号不能分辨。改进Music算法能在实现Music算法功能的基础上，分辨出相干信号源。

设阵列输出信号的协方差矩阵为

式中：

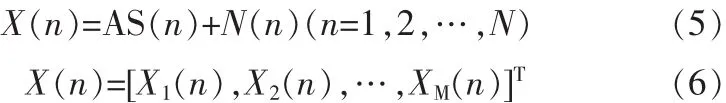
为M个阵元的输出。

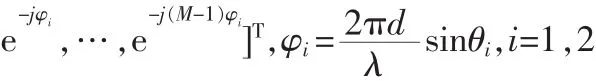
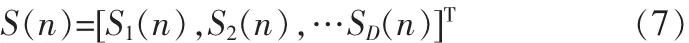
为入射信号向量；Si（n）是第i个信号源在阵元上的信号强度，即复振幅。

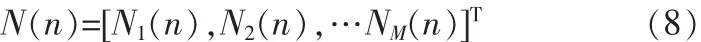
为噪声向量。其中：Ni（n）为零均值、方差为σ2的高斯白噪声，且与信号源不相关；N为采样数。

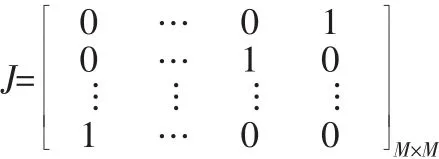
令J为M×M的反向单位矩阵，即

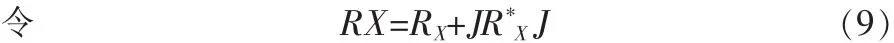
取Vn=U（：，D+1：M）为噪声特征值对应的特征向量，即噪声子空间。

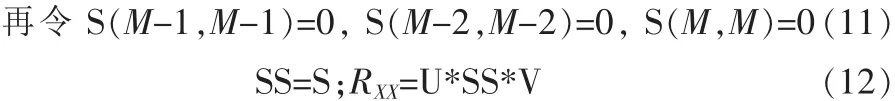
利用低秩逼近法，用一个低秩矩阵来代替满秩矩阵RX。

再对RXX进行分解，即：

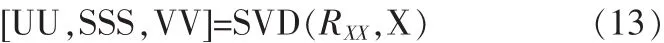
取Vnn=UU（：D+1：M）为噪声特征值对应的特征向量，即噪声子空间。

再对两次得到的噪声子空间向量进行平均，即：

此即为经过处理后的噪声子空间。再用这个噪声特征向量代入计算，Music算法就能有效地估计出信号的DOA了。这里的推导主要是从RX的数学特征上入手，使噪声子空间经过处理后能够与方向矢量充分正交，从而估计出信号的DOA。

3 改进Music算法的实现

现将改进Music算法的运算步骤归纳如下：

1） 收集输入样本X（i），i=1，…，N，估计输入协方差矩阵，即

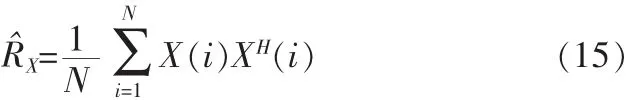
2）构造新的协方差矩阵RX，即：

式中：J为M×M的反向单位矩阵；为的共轭。

3）对上面得到的新的协方差矩阵RX进行特征分解，即：

取Vu=U（：，D+1：M）构造噪声子空间Vu。

4）再用低秩矩阵代替满秩矩阵RX，构造新的协方差矩阵，并进行特征分解，重复上述步骤，再一次构造噪声子空间Vnn。

5）计算两次得到的噪声子空间的平均，得到最后的噪声子空间VU，即：VU=（Vnn+Vn）/2 （18）

6）构造空间谱函数，即：

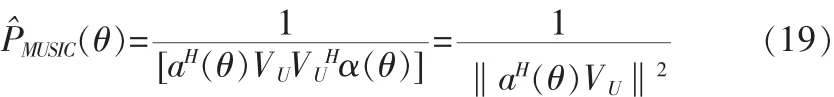
4 仿真结果及其分析

4.1 经典MUSIC仿真

1）仿真条件为：阵元数为n=8；阵元间距为 1/2波长；信号源数目为N=3， 信号源入射方向分别为-13°、-10°，35°，SNR1=20 dB和SNR2=5 dB采样数为1 000。如图1所示。

2）仿真二：仿真条件为：阵元数为n=8；阵元间距为 1/2波长；信号源数目为N=3信号源入射方向分别为-60°、35°，45°，其中 35°与 45°信号为强相关信号。 SNR=10 dB。采样数为1 000。如图2所示。

从图中可以看到，Music在信噪比降低和信号相关度较强的情况下分辨率较低，不能有效估计来波角度。

4.2 改进的Music算法仿真

仿真条件3：阵元数为n=8；阵元间距为 1/2波长；信号源数目为 N=3，信号源入射方向分别为-13°、-10°，35°，SNR=5 dB。采样数为1 000。

图1 不同信噪比下的Music算法空间谱Fig.1 Music algorithm space spectrum of different SNR

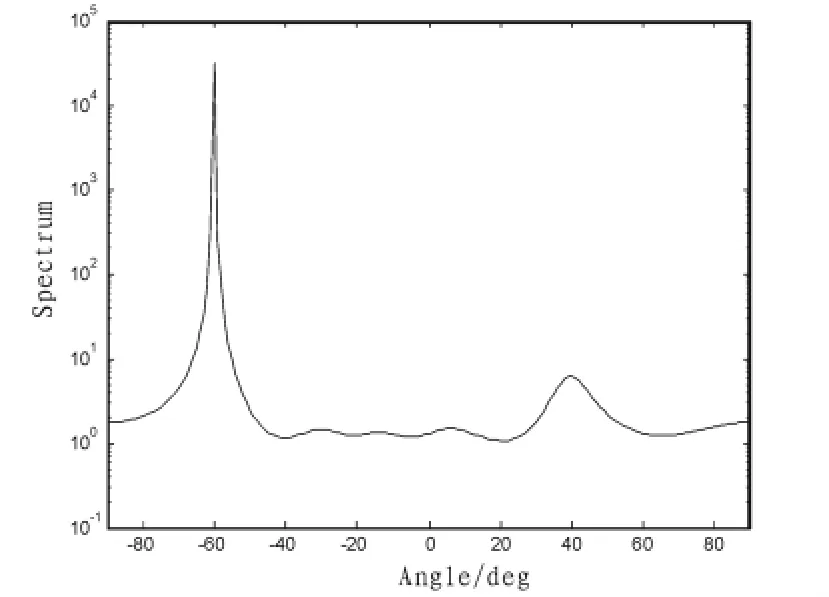
图2 强相关信号下的Music算法空间谱Fig.2 Music algorithm space spectrum of strong correlation signal

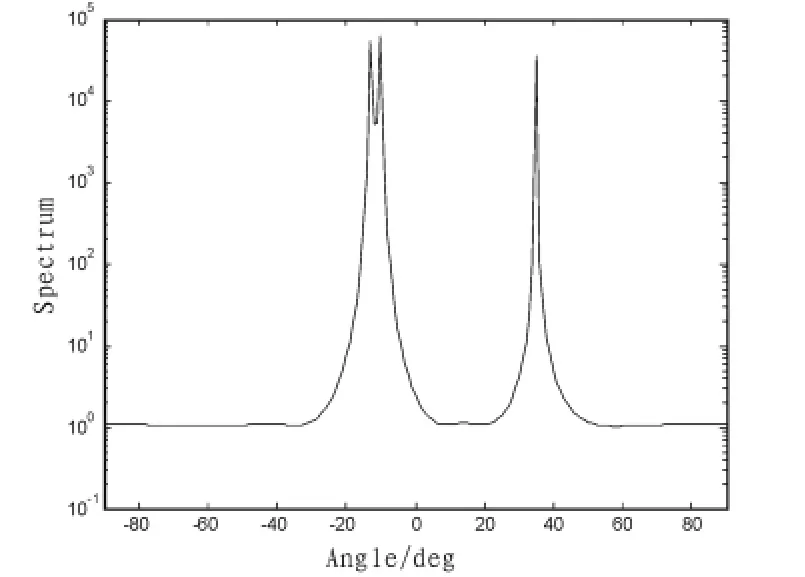
图3 信号间相差较小且信噪比为5 dB下的改进的Music算法的空间谱Fig.3 Improved Music algorithm space spectrum in SNR=5 and small signal interval

仿真4：仿真条件为：阵元数为n=8；阵元间距为1/2波长；信号源数目为 N=3 信号源入射方向分别为-60°、35°、45°，其中35°与45°信号为强相关信号。 SNR=10 dB。采样数为1 000。

较分析：通过图1和图2对比可看出，Music算法虽然可以精确地估计出各信号的波达角，但是随着信噪比的降低，空间谱的谱峰也在降低，当SNR=5时，Music算法不能分辨出-13°和-10°的信号。当存在强相关信号时，Music算法也不能分辨出强相关信号的波达方向，但改进的Music在信噪比低或信号相关的情况下均能很好的分辨出波达方向，并且性能更好。

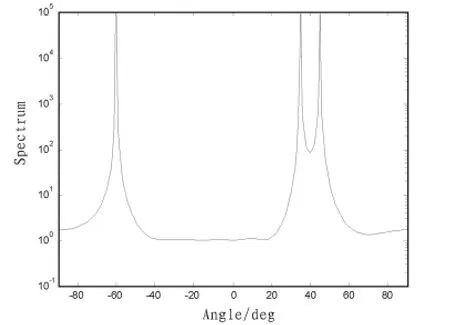
图4 强相关信号下的改进的Music算法的空间谱Fig.4 Improved Music algorithm space spectrum of strong correlation signal

5 结 论

文章对主要在针对经典Music算法不能很好的分辨强相关信号，而常用的空间平滑Music算法又以牺牲有效阵元数，且计算量过大的情况下，提出一种结合新的TOPELITZ和Music结合的算法，有效地解决了分辨率和算法复杂度的问题。实验也证明该算法的有效性。

[1]Bienvenu G，Kopp L.Decreasing high resolution method sensitivity by conventional beamformerpre-processing[C]//Acoustics， Speech， and Signal Processing， IEEE International Conference.San Diego.CA，USA，1984（9）：714-717.

[2]Shan T J，Waxm，Kailath.Ton spatial smoothing for direction of arrival estimation of coherent signals[J].IEEE Trans on ASSP，1985（33）：806-8111.

[3]WilliamsR T，Prasad S，MahalanabisA K，etal.An improved spatial smoothing technique for bearing estimation inamul2tipathenvironment[J].IEEETransonASSP，1988（36）：425-4321.

[4]Taga F，Shimotahira H.A novel spatial smoothing technique for the MUSIC algorithm[J].IEICE Transcommun，1995（78-B）：1513-1517.

[5]高书彦，王永良，陈晖.模式空间矩阵重构波束形成算法研究[J].电子与信息学报，2008，30（5）：1096-1099.

GAO Shu-yan，WANG Yong-liang，CHEN Hui.Model space matrix reconstruction beam-forming algorithm research[J].Journal of Electronics and Information Technology，2008，30（5）：1096-1099.

[6]熊键，董李梅.波束空问的超分辨测向算法研究[J].电子对抗，2007，30（2）：4-8.

XIONG Jian，DONG Li-mei.The super resolution direction finding algorithm research of beam space [J].Electronic Countermeasure，2007，30（2）：4-8.