基于MATLAB的PMSM混沌系统仿真

唐文，赵莉

（桂林空军学院 广西 桂林 541003）

永磁同步电动机 （Permanent Magnet Synchronous Motor，PMSM）由于其结构简单，高效节能，调速范围宽和波纹转矩小等优点，在高级轿车，航天，航空，计算机，通讯等各个行业得到广泛应用。在改变电机参数的条件下，电机会发生混沌现象[1]。混沌是发生在确定性系统中的一种不确定行为，混沌状态时平衡状态、周期状态、拟周期状态等以外的第4种状态[2]。张波等在研究了永磁同步电动机模型后，经过变换得到了一个适合分析永磁同步电动机混沌运动的模型[3]。文献[4]利用Lyapunov指数和容量维对该模型进行分析，进一步验证了永磁同步电动机中混沌运动的存在性。任海鹏等利用延迟反馈，控制永磁同步电动机的混沌现象[5]，韦笃取等利用微分几何理论中的状态反馈精确线性化，来控制PMSM中的混沌运动[6]。混沌现象的存在，将严重影响电机运行的稳定性，因而有必要对电机控制系统的混沌产生机理进行研究。MATLAB[7-8]中的Simulink的数值模拟及图形描绘给研究同步电动机混沌现象带来了方便。本文主要利用了MATLAB对永磁同步电动机进行仿真，验证了永磁同步电动机中混沌的存在。

1 基本分析

PMSM混沌系统的数学模型为：

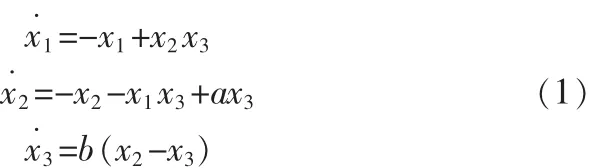
令a=28，b=3，显然系统（1）存在2个非线性项，在这个系统中状态变量分变为x1，x2，x3，为了求其平衡点，令：

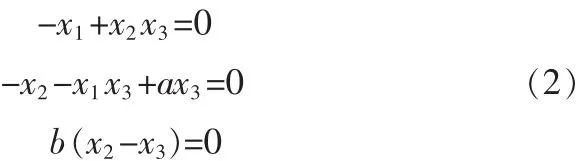
求解式（2），可得系统的 3 个平衡点：E0=（0 0 0）；E1=（27

在平衡点 E0=（0 0 0），对系统（1）进行线性化得 Jacobian矩阵为：

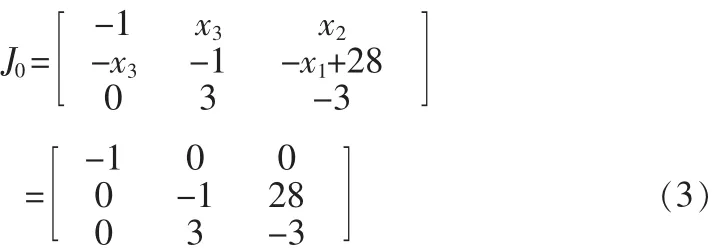
为了求系统相应的特征根，令：

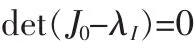
得其特征根为：λ1=-11.2195

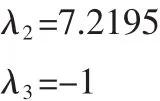
λ1和 λ3为负实根，而 λ2是正实根，因此平衡点 E0=（0 0 0）是不稳定的。

在平衡点 E1=（27），也对系统（1）进行线性化得Jacobian矩阵为：

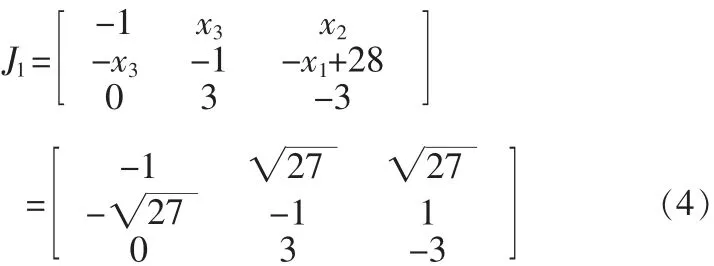
为了求系统相应的特征根，令：

得其特征根为：

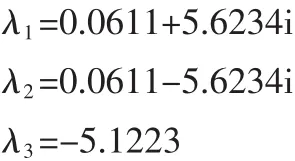
λ3为负实根，而λ1和λ2是一对具有正实部的共轭复根，由此可见它们也是不稳定的。

在平衡点E3=（27-），同样对系统（1）进行线性化得Jacobian矩阵为：

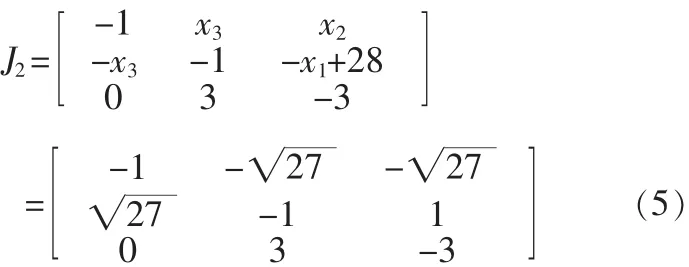
为了求系统相应的特征根，令：

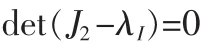
得其特征根为：

同样的，λ3为负实根，而λ1和λ2是一对具有正实部的共轭复根，由此可见它们同样是不稳定的。

从上述分析可知，系统（1）中的3个平衡点都是不稳定的。

2 PMSM混沌系统的动态仿真

MATLAB是由Math Work公司推出的一种面向科学与工程计算的高级语言，它集科学计算、自动控制信号处理、神经网络、图像处理等于一体，具有极高的编程效率。MATLAB提供的Simulink是一个基于Windows环境下的以图形进行编程的软件，可用来对动态系统建模、仿真和分析。同时，MATLAB语言编程直观易懂，MATLAB在数值计算及动态仿真等方面，研究人员不但工作量小，编程也很容易，开发周期也大大缩短，数据也更加直观，因此在混沌学领域中将发挥其重大作用。

本文在基于MATLAB环境，研究了离散混沌系统的数值解法和图形仿真。同时针对离散时滞混沌系统给出了数值仿真的MATLAB程序[9]。从数值仿真角度来说，本文所得方法对于离散混沌系统的混沌同步和控制仿真及误差描述都有积极的意义。

为了研究PMSM非线性动力学特性，首先用Simulink模型库构建仿真系统，将所需要用的单元功能模块（积分单元integrator，乘法单元 Product，求和单元 Add，相减单元Subtract，增益 Gain）拖入到 Untiled窗口中；按系统（1）所示的系统模型把模块连接起来，如图1所示。设系统初值为（10，10，0），仿真时间为 100 s，其他参数为默认值。 用 Scope（示波器）可分别观察到 x1，x2，x3的演化轨迹，如图 2所示。 用XY graph模块可观察系统在Y-Z平面的吸引子，如图3所示。

3 结束语

图1 PMSM混沌系统仿真模型Fig.1 Simulation model of PMSM chaotic system

本文对PMSM混沌模型进行了数学特征分析，发现该系统在特定参数情况下能够表现出丰富的混沌动力学行为。通过研究，MATLAB给PMSM模型的仿真研究提供了十分便利的平台，并且基于Simulink对该模型进行了仿真，仿真结果验证了该系统具有混沌的数学特征。

图2 PMSM混沌系统时序图Fig.2 The time-domain result of PMSM chaotic system

图3 PMSM混沌系统相图Fig.3 The phase result of PMSM chaotic system

[1]曹志彤，郑中胜.电机运动系统的混沌特性[J].中国电机工程学报，1998（5）：319-322.

CAO Zhi-tong，ZHENG Zhong-sheng.The chaos of nonlinear moving system for the synchronous motor[J].Proceedings of the CSEE，1998（5）：319-322.

[2]曲正修，张金春.混沌学研究进展评述[J].飞航导弹，2001（12）：30-33.

QU Zheng-xiu，ZHANG Jin-chun.Review of chaos research progress[J].Winged Missiles Journal，2001（12）：30-33.

[3]张波，庞敏熙.一类永磁同步电动机混沌模型与霍夫分叉[J].中国电机工程学报，2001（9）：13-17.

ZHANG Bo，PANG Min-xi.The chaotic model and Hopf bifurcation of a type of permanent-magnet synchronous motor[J].Proceedings of the CSEE，2001（9）：13-17.

[4]张波，李忠.利用Lyapunov指数和容量维分析永磁同步电机仿真中的混沌现象[J].控制理论与应用，2001（4）：589-592

ZHANG Bo，LI Zhong.Analyzing chantic phenomenon in permanent-magnet synchronous motors with lyapunov exponent and capacity dimension[J].Control Theory and Applications，2001（4）：589-592

[5]任海鹏，刘丁，韩崇昭.基于直接延迟反馈的混沌反控制[J].物理学报，2006（6）：2694-2701

RENG Hai-peng，LIU Ding，HAN Chong-zhao.Anticontrol of chaos via direct time delay feedback[J].Acta Physica Sinica，2006（6）：2694-2701.

[6]韦笃取，罗晓曙.基于微分几何方法的永磁同步电动机的混沌运动的控制[J].物理学报，2006（1）：54-59.

WEI Du-qu，LUO Xiao-shu.Controlling chaos in permanent magnet synchonousmotor based on the differential geometry method[J].Acta Physica Sinica，2006（1）：54-59.

[7]马茹，胡建伟，杨立成.GPS信号和其干扰的Matlab仿真[J].电子科技，2011（5）：17-22.

MA Ru，HU Jian-wei，YANG Li-cheng.The matlab simulation of the GPS signal and the interference[J].Electronic Science and Technology，2011（5）：17-22.

[8]杨金孝，朱琳.基于Matlab/Simulink光伏电池模型的研究[J].现代电子技术，2011（24）：192-194，198.

YANG Jin-xiao，ZHU Lin.Research on photovoltaic cell modelbased on matlab/simulink[J].Modern Electronic Technique，2011（24）：192-194，198.

[9]赵景波.Matlab控制系统仿真与设计[M].北京：机械工业出版社，2010.