高速成形滤波器的研究与实现

李艳萍，周胜源

（桂林电子科技大学 信息与通信学院，广西 桂林 541004）

随着现代数字通信技术的发展，频谱成形技术已成为一个重要研究课题。在高速传输系统中传输信道的带限和非线性两大特性，对发送信号的频谱也提出了较高要求。为了节约频谱资源，需要对发射的基带信号进行带限；为使传输误码率足够小，必须最大限度减小码间串扰（ISI）。频谱成形常常在基带实现，压缩基带信号频谱的主要方法就是采用基带成型滤波器[1]。基带成形可以采用模拟滤波器实现，也可采用数字滤波器实现。数字滤波器已成为当代 DSP算法中的基本设计之一，正在取代传统的模拟滤波器，而这种软件算法的基于FPGA实现则更有现实意义，FPGA由于其高速和可多次编程的特性而成为各种系统的首选，但是由于其内部资源的限制和结构特点，研究合理和优化的算法既有利于算法实现和速度提高，又有利于节省硬件资源。分布式算法的引入，极大地减少了对FPGA的资源占用，有效的提高了FPGA的内部资源的利用率，通过对分布式算法的改进，可有效地在资源运用和提高速度两者之间进行取舍[2]。

1 成形滤波器原理

1.1 函数确定

实际系统中，广义信道传递函数H（f）由发送滤波器HT（f）、信道HC（f）、收滤波器HR（f）3 部分共同构成[1]，即：

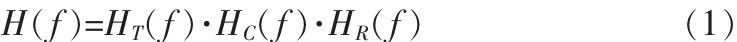
根据 Nyquist第一准则，当H（f）幅频特性满足的滚降系数为α升余弦滤波器特征，即发送端成形滤波器在频域上具有平方根升余弦滚降特性，与接收端的匹配滤波器级联后在频域上具有升余弦滚降特性时，可以实现无ISI传输时刻降低对采样时钟精度的要求，当信号噪声可以忽略时，取HC（f）≈1，按照接收滤波器的输出信噪比最大准则，有：

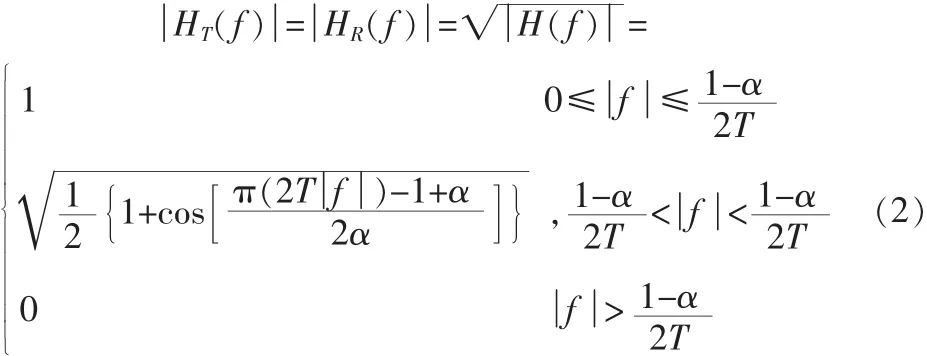
式中：T为输入码元的周期；α为滚降系数。α定义：α=fa/f0，滚降特性信道的带宽为fa+f0=（1+α）f0。 滚降系数越大，频谱在截止频率处越光滑；而频带利用率越低。记f0=1/2T，由上式可推出滚降系数为α平方根升余弦冲击响应为：

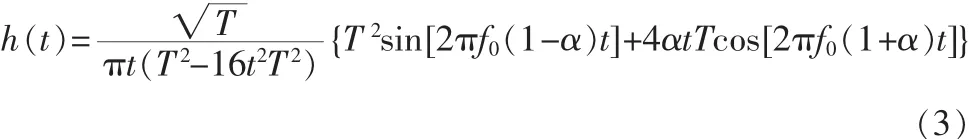
1.2 参数设置

在设计成形滤波器之前，有许多参数需要确定，先通过Matlab（FDATOOL工具）仿真，得出不同参数对信号传输误码率的影响（卫星通信要求：第一旁瓣的高度低于-40 dB，杂散频率低于-60 dB），寻找最佳的参数，同时还要兼顾具体硬件实现的难易程度。 本次设计选取 L=8，M=8，α=0.5，fs=600 MHz，fc=75 MHz阶数N=33的SRRC FIR滤波器。可得出系数h（0），h（1）h（2）.....h（31）h（32）的数值。

1.3 多相结构

本次研究的针对的高速数传系统是卫星通信，设置基带速率为150 Mbps，该成形滤波器的采样速率为4×150=600 MHz，就现有的FPGA中直接进行600 MHz这么高速率的滤波运算是不可能的。由信号处理[2]知识知，在4倍采样的条件下，FIR成形滤波器相当于一个4倍的内插滤波器。其实现结构可以采用多相结构，一方面可以减少运算负担，提高运算速度，另一方面也可减小滤波运算的累积误差，提高计算精度，降低滤波器的运算速率。

在FIR滤波器中，转移函数为：

式中N为滤波器长度。将冲激响应h（n）按下列的排列分成M个组[3]，并设N为M的整数倍，即N/M=Q，Q为整数，则：

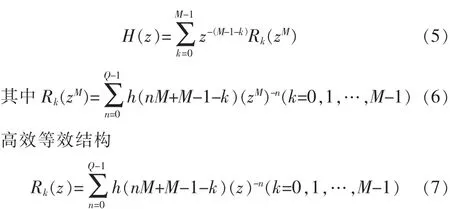
由此得出多相内插滤波器高效等效结构和等效的开关结构分别如图1、图2所示。

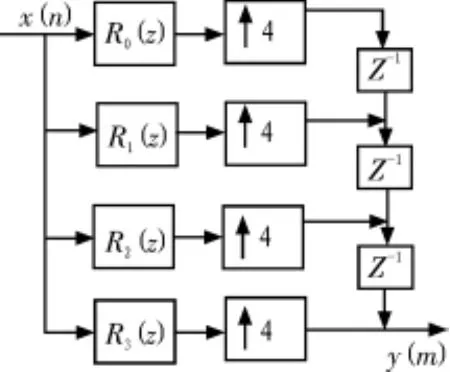
图1 多相内插滤波器高效等效结构图Fig.1 Efficient equivalent structure of Polyphase interpolation filter

图2 多相内插滤波器开关结构Fig.2 Switch structure of Polyphase interpolation filter

关于多相滤波器的设计往往限制原型内插滤波器的长度N是内插倍数M的整数倍，则多相子滤波器将是长度为N/M的FIR滤波器。但本次设计针对的是根升余弦滤波器的阶数N=33.M=4，N与M不成整数倍关系，鉴于分数倍的复杂度，现针对滤波器的系数进行优化处理。

在数字化波形成形时，为确保h（t）采样后的h（n）保持第一类线性相位，可舍去h（t）|t=0样点，同时对N-1（偶数）点h（n）右移 N-1/2[4]。

根据该思想，针对本次设计，即舍去原滤波器的系数h（0），修改后的对称系数[5-6]，

由一个33阶的滤波器演变成由4个并行的8阶子滤波器构成。 观察上述系数得：R0（Z），R3（Z）包含的元素相同而排列顺序正好相反，一般称之为镜像对称（互为镜像对称），R1（Z），R2（Z）也互为镜像对称。如何利用这种对称特性对各个子滤波器进行优化，具体方法不做介绍。

2 DA算法

分布式算法（DA）巧妙的利用 ROM查找表将固定系数的乘累加运算转换成查找表操作，避免了乘法运算。同时，查找表后的数据执行的都是简单的加法运算，可以较大程度地提高运算速度和插入流水。这种方法是目前比较常用的基于FPGA设计FIR滤波器的方法。传统DA算法当N增大时，查找表的规模将呈指数倍增加，单个的查找表是完成不了的。并且当位数B增大时，累加运算也将增加，导致工作速度降低。“改进的分布式算法”[7]主要针对两个方向：第一个改进是缩小查找表规模，第二个改进是提高速度。

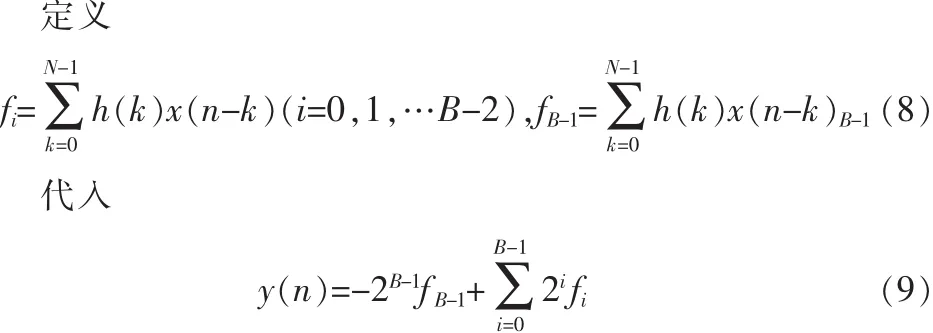
为了分析的方便，且与 FPGA的 4输入 LUT相关，假定N为 4的整倍数。将fi作如下变形，得：

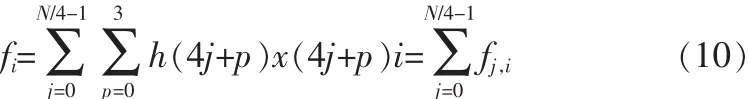
可得到了fj，i的查找表，于是将fi的大查找表转化为 N/4个基于fj，i的查找表，所需ROM的大小也大大降低。

本次研究DA算法针对4个并行8阶子滤波器，则每个子滤波器各自使用改进DA算法实现。在速度与硬件规模权衡之下采用1BAAT和2个查找表的方法结合使用，每个查找表使用并行结构实现。

3 FPGA实现

3.1 总体框架

各部分主要模块功能[8]

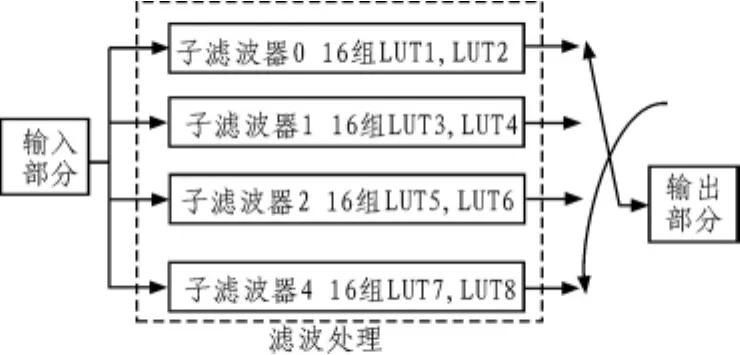
图3 FPGA实现总体框图Fig.3 Overall diagram of FPGA implementation

1）输入部分

这个模块主要是负责向滤波器模块传输数据x（n），并且产生滤波处理模块、查找表、输出模块的控制时钟。

2）核心滤波

这个模块主要是利用改进的DA算法实现4个并行滤波器。每个子滤波器的大查找表分割成为2个小查找表，每个小查找表再利用并行结构实现.

3）输出部分

该模块是结合内插滤波器的开关结构而设计的，以达到输出的时钟是输入时钟4倍的一个内插过程。

3.2 仿真结果

在ISE和Modelsim的联合建模仿真下，结果表明成型滤波器成功，仿真图中有短暂的时延。

4 结束语

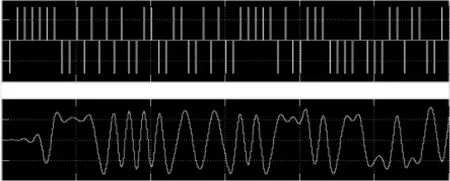
图4 仿真结果图Fig.4 Results of simulation

文中介绍了成形滤波的原理和设计数字滤波器的基本步骤。该滤波器满足平方根升余弦的频率特性，采用多相结构实现高速基带成形滤波，打破了硬件限制，实现了数据的高速处理。基于FPGA的改进式DA算法分布式算法的引入，极大地减少了对FPGA的资源占用，有效的提高了FPGA的内部资源的利用率，有效地在资源运用和提高速度两者之间进行取舍。

[1]曹志刚，钱亚生.现代通信原理[M].北京：清华大学出版社，2004.

[2]皇甫堪，陈建文，楼生强.现代数字信号处理[M].北京：电子工业出版社，2003.

[3]宗孔德.多抽样率信号处理 [M].北京：清华大学出版社，1996.

[4]赵林军.根升余弦脉冲成形滤波器FPGA实现[J].现代电子技术，2011，34（1）：23-28.

ZHAO Lin-jun.FPGA implementation of square root raised cosine pulse shaping filter[J].Modern Electronics Technique，2011，34（1）：23-28.

[5]李增红，何攀峰，时惠.多相滤波在脉冲成形中的应用[J].仪器仪表学报，2010（8）：330-332.

LI Zheng-hong，HE Pan-feng，SHI Hui.Polyphase filter in the application of pulse shaping[J].Chinese Journal of Scientific Instrument，2010（8）：330-332.

[6]Vaidyanathan P.Multirate digital filters，filterbanks，polyphase networks and applications[J].Proc.IEEE，1990，78（1）：56-93.

[7]李文刚，基于FPGA的高速高阶FIR滤波器设计[D].成都：电子科技大学，2005.

[8]KING Myung Soon，CHUNG Jin Gyun.Look-up table based pulse shaping filter [J].Electronics Letters，2000，36（17）：1505-1507.