基于BA无标度的复杂有向网络演化模型
2012-07-13马秀娟
马秀娟
(青海师范大学 计算机科学学院,青海 西宁 810008)
当前,各国研究人员在无向网络的拓扑结构特征,建立无向网络模型以帮助人们理解真实系统中各种宏观性质的微观生成机制,研究具有不同结构的无向网络中发生的各种动力学过程的特征,比如研究流行病的传播行为在无标度网络和指数网络中分别具有什么特征等方面已经取得了很大的进展,获得了许多令人兴奋的结果[1]。但以上研究大多是基于无向网络的,然而现实世界中许多复杂系统更适合于利用有向网络来表示和研究,这些复杂系统广泛的存在于科技、信息、社会及生物领域中,于是对有向网络基本理论及其应用的研究具有重要的实际意义。近年来,研究者们对有向网络进行了相对广泛的研究,他们通过实证万维网、细胞网络、电话网、引文网及食物网等有向网络而发现了它们的一些特征,并在此基础上提出了一些有向网络模型,研究了这些模型的特点及其简单应用[2-15]。例如,B.Tadic[12]等人提出了一个表示WWW网的有向网络模型;A.Ramezanpour[13]等人对发生在有向网络中的传播进程进行了研究;N.Schwartz[14]等人研究了有向无标度网络中的逾透问题;日本的TetsuroMurai[15]等人对有向网络的谱的性质进行了初步的研究。
近年来,随着对有向网络研究的逐步深入,研究者发现对有向网络的研究将有助于人类对与有向网络相关的许多领域有更深入的理解。对在信息通信、网络搜索、信号传输、传染病控制,网络的安全性和可靠性等方面都具有重要而深远的意义[16-20]。
1999年 Barabási和 Albert提出 Scale-free (无标度)网络模型[21]。与古典模型相比,这种模型较好地解释了一些实际网络(如因特网和演员合作网等)的特性。研究人员对大量的实际网络进行了实证分析[22,23],发现许多网络都具有无标度的特性。
上述网络模型是基于无向网络建立的,文中根据BA无标度网络模型提出了一种具有无标度特性的有向网络演化模型,并设计程序进行了仿真实验,对有向网络的度分布进行了分析,结果表明,利用文中提出的有向网络演化模型生成的复杂有向网络的度分布符合幂律分布,能有效的模拟现实世界的具有无标度特性的复杂有向网络,可以在此模型上展开对复杂有向网络的其他相关拓扑性质的分析及研究。
1 有向网络及其相关概念
1.1 有向网络
一个具体的网络可以抽象为一个由点集V边集E组成的图G=(V,E)。 节点数记为N=|V|,边数记为M=|E|,E中每条边都有V中一对顶点与之相对应,如果任意点对(i,j)与(j,i)对应同一条边,则该网络成为无向网络(undirected network),否则称为有向网络(directed network)[24]。图1给出了两种不同类型的网络。
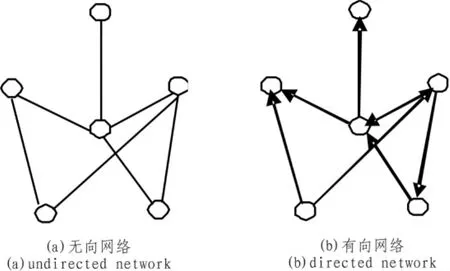
图1 不同类型网络结构图Fig.1 Different types of network structure
1.2 有向网络的度、出度、入度和邻接矩阵
节点i的度deg ree(i)定义为与该节点连接的其他节点的数目[25]。有向网络中一个节点的度分为出度(out-degree)和入度(in-degree)。节点的出度是指以该节点为弧尾指向其他节点的边的数目,记作deg-(i)-;节点的入度是指以该节点为弧头由其他节点指向该节点的边的数目,记作deg+(i)。特别地,在有向网络中 deg ree(i)=deg+(i)+deg-(i)。 从直观来看,一个节点的度越大就意味着这个节点在某种意义下相对重要。
设G是含有P个节点 (或顶点),q条有向边的有向网络。令

则称由元素 mij=(i=1,2,…p,j=1,2,…q)所构成 p×p 的矩阵为有向网络G的邻接矩阵,记作D。
2 BA无标度复杂有向网络演化模型
1999年Barabási和Albert[21]提出了一个以增长和择优连接机理演化的无标度网络模型,它揭示了各类现实网络最普遍的现象,但该模型只是一个无向的网络模型,它无法体现有向网络的一些主要特性,为了研究有向网络的相关性质,需要建立有向网络的动态演化模型以模拟现实世界中的复杂有向网络。文中在前人提出的BA无标度网络模型的基础之上提出了具有无标度特性的复杂有向网络演化模型。具体演化过程如下:
1)初始网络:初始给定m0个节点,m0条有向边,首尾连接,保证网络的连通性;固定网络的规模为N。
2)增长机制:每一时刻将N-m0中的一个节点s作为新节点加入到有向网络中。为了保证有向网络的连通性,结点s连入网络时,增加以结点s为弧尾的min条入边和以结点s为弧头的mout条出边;网络中不允许重连边,也不允许自身连边;新节点连接到网络后,N减1;
3)择优机制:新节点s连入网络时,将与网络中的已有结点进行连接,由于网络是一个连通的复杂有向网络,因此连接时考虑如下两个方面:
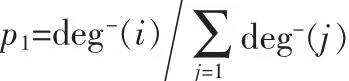
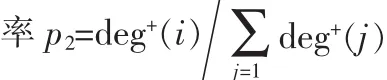
4)输出数据:输出最终得到的N个节点的邻接矩阵,该矩阵表示了利用上述演化模型生成的规模为N的复杂有向网络,同时输出该有向网络结点的度分布图,有向网络中结点的度为 deg ree(i)=deg+(i)+deg-(i),(其中 deg+(i)表示结点i的入度,deg-(i)为结点 i的出度)。
图 2 显示了当 N=5,m0=4,min=3,mout=1 时的 BA 无标度有向网络的演化过程。

图 2 BA 无标度有向网络演化示意图(N=5,m0=4,min=3,mout=1)Fig.2 BA scale-free directed network diagram evolution(N=5,m0=4,min=3,mout=1)
3 仿真结果及分析
文中通过计算机利用matlab程序设计语言,编写程序对上述演化模型进行了仿真实验。模拟了10 000个节点的BA无标度复杂有向网络模型,并得到了该复杂有向网络的邻接矩阵及网络中结点度分布图如图3所示。实验中的相关数据为网络的规模N=104,初始网络中的结点数m0=4,新节点连入网络时以该节点为弧头的入边min=3,以新节点为弧尾的出边mout=1。图中星号表示实验得到的数据(30次实验的平均值),直线是对于双对数图的拟合直线,可以看出通过上述BA无标度复杂有向网络演化模型得到的复杂有向网络的度分布满足幂指数为-3的幂律分布,具有明显的无标度特性。
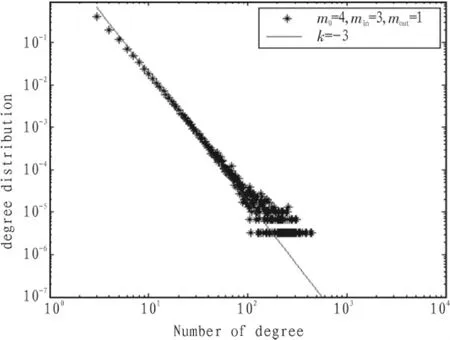
图3 BA无标度复杂有向网络的度分布Fig.3 Degree distribution of BA scale-free comple direction network
4 结 论
现实世界中有很多网络都是有向网络,例如神经网络、电子邮件网络等,文中提出的有向网络演化模型,对于研究复杂有向网络的相关特性具有重要的意义。通过仿真实验,本模型得到的复杂有向网络具有明显的无标度特性,能有效的模拟现实世界的具有无标度特性的复杂有向网络,可以在此模型上展开对复杂有向网络的其他相关拓扑性质及其动力学行为的分析及研究,依据本模型得到的仿真数据对于我们更进一步了解复杂有向网络具有重要的参考价值。
[1] Ralbert,Albarabasi. Statistical mechanics of complex networks[J].Rev.Mod.Phys,2002,74(1):32-35.
[2]Newman M E J.The strueture and function of complex networks[J].SIAM Review,2003(45):167-256.
[3]ErdosP,RenyiA.On random graphs[J].Publications Mathematicae,1959(6):290-297.
[4]Erdos P,Renyi A.On the evolution of random graphs[J].Pub.Math.inst.hung.Acad, sci,1960(5):17-61.
[5]Erdos P,Renyi A.On the strength of connectedness of a randomgraphs[J].ActaMath.Sci.Hungary,1961(12):261-267.
[6]Barabási,A.-L,Albert R.Emergenee of scaling in random networks[J].Scienee,1999(286):509-512.
[7]Barabási A L, Albert R, Jeong, H.Scale-free characteristics of random networks:The topology of the World Wide Web[J].Physica A,2000(281):69-77.
[8]Barabási A L ,Bonabeau E.Scale-Free Networks[J].Scientific American,2003(288):60-69.
[9]Newman M E J,Moore C,Watts D J.Mean-Field Solution of the small world network model[J].Physical Review Letters,2000,84(14):3201-3204.
[10]Watts D J,Strogatz S H.Collective dynamics of“smallworld”networks[J].Nature,1998(393):440-442.
[11]Barthelemy M L,AmaralA N.small-world networks:Evidence for a crossver picture[J].Phys.Rev, Lett,1999(82):3180-3183.
[12]Tadie B.Dynamies of directed graphs:the world-wide web[J].Physical A,2001(293):273-284.
[13]Ramezanpour A,Karimipour V.Simple models of smallworld networks with directed Links[J].Phys.Rev.E,2002(66):036-128.
[14]Schwartz N,Cohen R,Ben-Avraham D A.et al.Havlin.Percolation in directed scale-free networks [J].Physical review E,2002(66):151-442.
[15]Murai T.Master thesis:SpectralAnalysisofDirected Complex Networks[D].Japan:Tokyo,2002.
[16]De Angelis D L.Stability and connectance in food web models[J], Ecology,1975(56):238-243.
[17]J E C.Ratio of Prey to Predators in community food webs[J].Nature,1977(270):165-167.
[18]Morelli L G.Simple model for directed networks[J].Physical Review,2003(67):66-107.
[19]Siganos G,Faloutsos M,Faloutsos P, et al.Power-laws and the AS-level Internet topology [J].IEEE/ACM Trans.on Networking,2003(11):514-524.
[20]郭进利.供应链型网络中双幂律分布模型[J].物理学报,2006,55(8):3916-3921.
GUO Jin-li.The bilateral power-law distribution model of supply chain networks[J].Acta Phys.Sin.,2006,55 (8):3916-3921.
[21]BarabásiA L, AlbertR.Emergence ofscaling in randomnetworks[J].Science,1999,286(5439):5092512.
[22]Dorogovtsev S N,Mendes J F F.Evolutionof networks[J].Adv.Inphys.,2002(51):1079-1187.
[23]Strogatz S H.Exploringcomplex networks[J].Nature,2001(410):268-276.
[24]汪小帆,李翔,陈关荣.复杂网络理论及其应用[M].北京:清华大学出版社,2006.
[25]王朝瑞.图论[M].2版.北京:北京理工大学出版社,2000.
[26]杨韬,刘崇新,许喆,等.基于神经网络与混沌理论的电力系统短期负荷预测[J].陕西电力,2008(6):6-9.
YANG Tao,LIU Chong-xin,XU Zhe,et al.Short-term load forecasting based on Chaos theory and neural network in power system[J].Shaanxi Electric Power,2008(6):6-9.
