基于非参数核密度估计的中国水果市场收益率分布研究

李干琼，许世卫，李哲敏，董晓霞

（中国农业科学院农业信息研究所 农业部智能化农业预警技术重点开放实验室，北京 100081）

0 引言

我国是世界水果生产大国，产量多年稳居世界第1。水果产业在我国农业产业中占据重要地位，是继粮食、蔬菜之后的第三大农业种植产业，也是许多地方农民致富的支柱产业。近年来我国农产品市场波动风险加大，包括水果在内的多种农产品市场价格循环涨跌时有发生。2006年上半年猪肉价格持续下跌，2007年下半年出现暴涨，2009年上半年又大幅度下降，2010年低位运行，2011年又出现暴涨，据农业部监测2011年7月份全国批发市场猪肉价格涨至每公斤26.0元以上，价格波动如此之大实属罕见。近两年尤为突出，2010年上半年相继出现大蒜、玉米、辣椒、绿豆、生姜等农产品价格暴涨，再到下半年的棉花、白糖、苹果的大幅上涨；2011年4月份山东卷心菜价格一度跌至每斤8分钱，5月份海南香蕉经历了过山车，香蕉价格一个月内从每公斤6.8元跌至1.2元。在我国经济走向市场化、国际化的今天，较大的农产品市场风险已严重影响到农业的稳定和国计民生。因此，科学分析我国水果市场收益率分布（或称市场价格波动率分布），有助于准确分析与研判市场价格风险，为农业管理部门提供决策依据。

1 研究方法

1.1 核密度估计方法

假设变量x的概率密度函数为f(x),且f(x)=F'(x)，∫f(x)dx=1，则有：

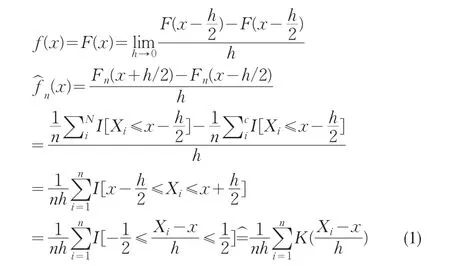
其中，K（·）为kernel函数，K(u)=I(||u≤1/2)，满足条件：∫K(x)dx=1;∫xK(x)dx=0;∫x2K(x)dx＜∞ 。h为窗宽（bandwidth）。可知，核密度估计需要选择核函数和窗宽。常见的kernel函数有以下4种：

③二次核函数（Quadratic kernel(p=4)）:

④三角核函数（:K(x)=(1-|x)I|x|≤1

1.2 窗宽的选择方法

选择合适的窗宽是核函数密度估计的关键所在。理论上，最优窗宽的选择是基于估计密度与真实密度之间误差最小来考虑的，即的MSE最小。MSE可表示如下：

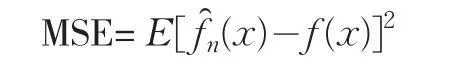
可以证明：

当n→∞时，h→0，nh→∞，这时有

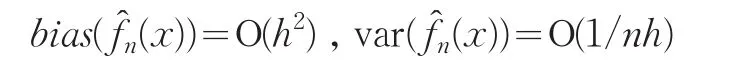
故式(2)又可表示为：

在实际应用中，常用的窗宽选择方法有4种：least squares cross-validation method（简称LSCV法;Rudemo,1982;Bowman,1984）、拇 指 法(rule-of-thumb;Silverman,1986)、插 入 法 (plug-in)、LCV 法 (likelihood cross-validation)。本研究最优窗宽h的选择采用LSCV法，即ISE满足：

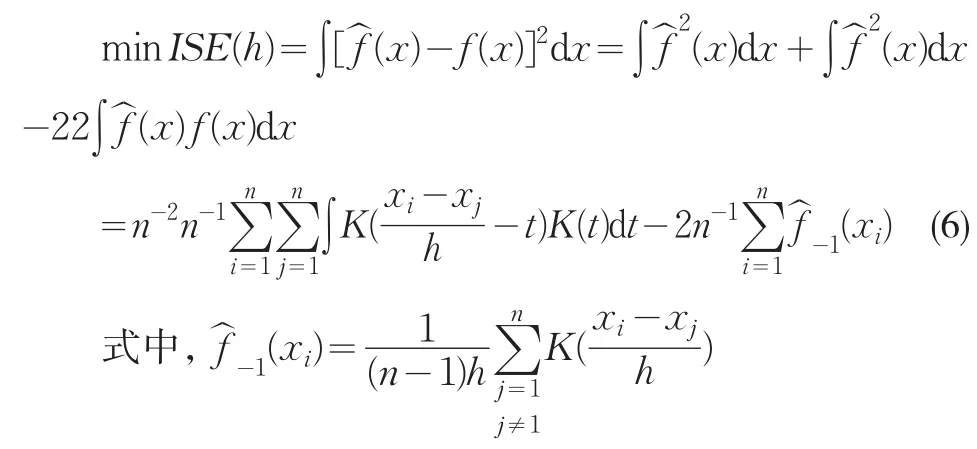
式（6）中的窗宽h初始值选取可采用采用拇指法确定，即h1=1.06σn-1/5或h2=0.9An-1/5，其中A=min(σ,R/1.34)，σ是样本标准差，R是上分位数（0.75）和下分位数（0.25）的区间值。由于σ易受样本离群数据(outliers）的影响，故采用h2作为初始值。由于密度函数估计结果对窗宽h的选择更为敏感，而对核函数的选择不敏感，因此本研究中kernel函数采用高斯函数。

1.3 市场价格波动区间的风险概率估算

采用核密度估计得到农产品市场收益率的概率密度函数后，累积概率密度函数可表示为依据指定的波动区间，可计算相应的概率为：

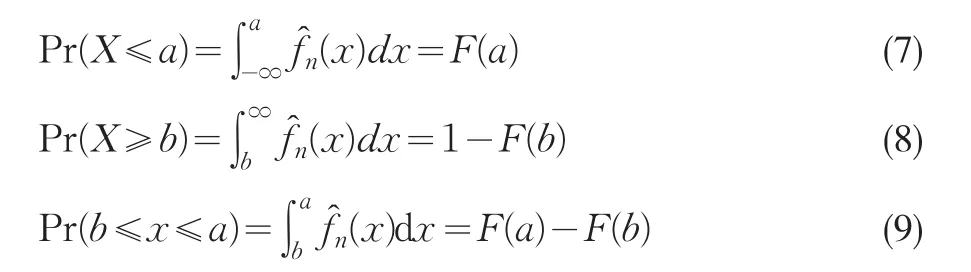
2 数据说明

本研究水果主要包括富士苹果、甜橙、鸭梨、国光苹果、蜜桔、香蕉、西瓜、菠萝、脐橙、巨峰葡萄、芦柑、桃子等12个品种。原始价格数据来源于农业部522个定点批发市场的日价格监测数据，全国日批发市场价格为522个批发市场大宗价的加权平均，全国月度批发市场价格采用全国日价格的平均值，数据起止期间为2000年1月～2010年12月。

关于市场收益率的表示方法有算术收益率和对数收益率两种方法，本质上没有区别，也不影响收益率分布的估计。本研究采用算术收益率表示（价格波动率），用Pi,t（i=1,2,…,12）分别表示12种水果的价格序列，则收益率可表示为：Ri,t=(Pi,t-Pi,t-1)/Pi,t。

表1为水果品种市场收益率（价格波动率）的基本统计量。可以发现：1）富士苹果、鸭梨、脐橙市场收益率为偏度值为负，表明其市场收益率的概率密度分布为左偏分布，其他9个品种为右偏分布；2）12个水果品种的峰度值均大于3，表明都呈“尖峰厚尾”分布。3）标准差来看，桃子价格波动最为剧烈，其次为甜橙；（4）JB统计量表明，甜橙、鸭梨、蜜桔、西瓜、芦柑和桃子等市场收益率明显不服从正态分布。

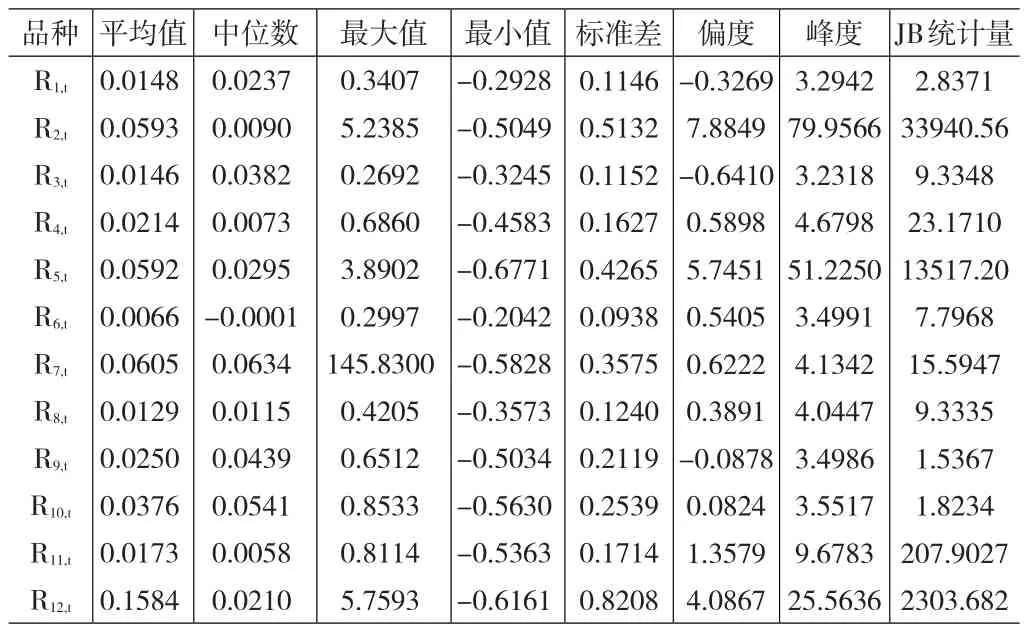
表1 水果市场收益率基本统计量分析

3 结果分析

本研究采用的软件为R2.11.1，结果如下：

3.1 窗宽的确定。

根据序列Ri,t，采用LSCV法和拇指法确定的窗宽如图1所示。其中，hopt表示根据LSCV法确定的最优窗框，h表示根据拇指法确定的窗框。由CV曲线图可以看出（根据式（6）计算），大多数情况下拇指法确定的窗框h不是最优的，只有CV值为曲线最低点时所确定的窗宽才是最优的。图1表明，只有富士苹果和国光苹果采用两种方法确定的窗宽是无差异的，其他品种由LSCV法确定的窗宽都要优于拇指法。

图1 基于LSCV法和拇指法确定的不同水果品种窗宽比较

图2 不同水果品种市场的收益率分布

3.2 收益率分布

根据最优窗宽值（hopt），得到不同水果品种序列Ri,t的概率密度分布如图2所示。从中可以看出，只有富士苹果和国光苹果比较接近正态分布，其他水果品种呈现“尖峰厚尾”分布比较明显。其中甜橙、蜜桔、桃子等的收益率分布相类似，为明显的右偏分布。

3.3 概率密度函数

根据窗宽和核函数，由式（1）得到不同水果品种市场收益率（价格波动率）的概率密度函数分别如下：

3.4 波动区间的概率值。

根据式(7)、式(8)和式(9)，计算的全国不同水果品种批发市场价格波动区间的概率值见表2。水果价格波动区间的制定参照了农业部有关农产品价格波动幅度界定标准，将监测预警的警级划分为4个等级，即无警(0～±5%，用绿灯表示)、弱警(±5%～±10%，用蓝灯表示)、中警(±10%～±15%，用黄灯表示)和强警(±15%以上，用红灯表示)。表2可以得出几点结论：1）大多数水果品种涨价的概率高于降价的概率，即出现价格上涨的概率在50%以上；只有香蕉和芦柑的涨跌风险基本相当；2）从全国不同水果品种出现强警（红灯区域）的情况来看，桃子的风险最大，出现概率高达69.93%；其次为西瓜，出现强警的概率为67.70%；巨峰葡萄和甜橙涨跌幅度在15%的概率也都在50%以上；香蕉的风险最小，出现强警的概率仅为9.76%。

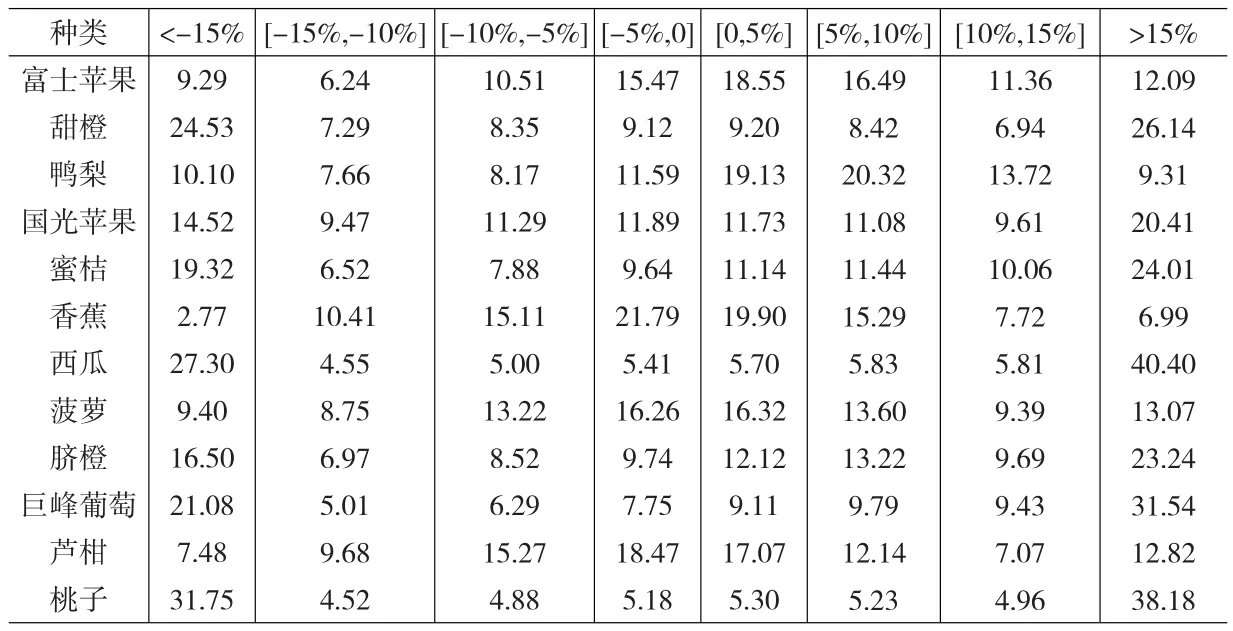
表2 全国水果批发价格波动区间的概率值

4 主要结论与讨论

4.1 结论

通过本研究，可以得出以下基本结论：非参数核密度估计结果表明，不同水果品种的市场收益率分布存在差异，且不服从的正态分布，尤其甜橙、鸭梨、蜜桔、西瓜、芦柑和桃子等与传统经验分布差异大；水果的市场收益率分布是不对称的，本研究的水果品种中有10种涨价的风险要大于降价的风险，即涨价的概率为50%以上，只有香蕉和芦柑2个品种的涨跌概率基本相当；水果总体上属于季节性产品，不同上市季节价格差异较大，也即价格季节性波动尤为明显，从全国不同水果品种出现强警（红灯区域）的情况来看，桃子的风险最大，出现概率高达69.93%；其次为西瓜，出现强警的概率为67.70%；香蕉的风险最小，出现强警的概率仅为9.76%。

4.2 需要说明的问题

本研究采用非参数核密度估计得到了12种水果品种价格波动的概率密度分布，与传统的参数估计结果相比更为准确，但也都是非条件的概率密度分布。条件概率密度分布（conditional density）能够提供更加充分的信息，而农产品市场领域关于这方面的研究刚刚起步。

[1]Izeman AJ.Recent Developments in Nonparametric Density Estimation[J].Journal of the American Statisti⁃cal Association,1991,86(413).

[2] Jones MC,Marron JS,Sheather SJ.A Brief Survey of Bandwidth Selection for Density Estimation[J].Journal of the American Statistical Association,1996,91(433).

[3] Cao R,Delgado MA,Gonzalez-manteiga W.Nonpara⁃metric Curve Estimation:an Overview[J].Investigacions Economicals,1997,(2).

[4] Li Q,Racine J.Nonparametric Estimation of Distribu⁃tions with Categorical and Continuous Ddata[J].Journal of Multivariate Analysis,2003,（86）.

[5] Li Y,Singii RS,Sun YG.Goodness-of-fit Tests of a Pa⁃rameric Density Functions:Monte Carlo Simulation Studies[J].Journal of Statistical Research,2005,39(2).

[6] Shabri A.Nonparametric Kernel Estimation of Annual Maximum Stream Flow Quantiles[J].Matematika,2002,18(2).

[7] 陈启欢.中国股票市场收益率分布曲线的实证[J].数理统计与管理,2002,21(5).

[8] 封建强,王福新.中国股市收益率分布函数研究[J].中国管理科学,2003,11(1).

[9] 唐林俊,杨虎.沪深股市收益率分布特征的统计分析[J].数理统计与管理,2004,23(5).

[10] 曹志广，王安兴，杨军敏.股票收益率非正态性的蒙特卡罗模拟检验[J].财经研究,2005,31(10).

[11] 张峭,王川,王克.我国畜产品市场价格风险度量与分析[J].经济问题,2010(3).

[12] 王川.基于VaR的我国粮食期货市场基差风险度量与分析[J].农村经济与科技,2010，(7).

[14] 谭英平.非参数密度估计在个体损失分布中的应用[J].统计研究,2003，(8).

[15] 梁来存.我国粮食单产保险纯费率厘定的实证研究[J].统计研究,2010,27(5).

[16] 李干琼，许世卫，李哲敏等.中国蔬菜市场价格短期波动与风险评估[J].中国农业科学,2011,44(7).