基于可能度优势关系的区间序粗糙集模型*
2012-07-12徐智明陈小卫
徐智明 刘 宏 马 琳 陈小卫
(1.92819部队 大连 116600)(2.海军驻航天一院军代室 北京 100076)(3.海军军训器材研究所 北京 100841)(4.海军航空工程学院 烟台 264001)
1 引言
粗糙集理论[1]是分析和处理各类信息的有效工具,已成当前研究的热点,被广泛知识发现、数据挖掘、决策分析等领域中[2~4]。在多属性决策中,属性值往往具有偏好关系,基于等价关系的经典粗糙集则难以满足需要。于是,Greco等[5~7]对粗糙集理论进行扩充,利用优势关系来代替等价关系,提出了基于优势关系的粗糙集,为多属性决策提供了一种新方法。
然而在多属性决策过程中,属性值往往难以用精确数来表达。区间型多属性决策则是多属性决策的一种特殊情况。在区间信息系统上基于优势关系的粗糙集方法已有研究。文献[8]将属性值具有偏好关系的区间值信息系统称区间序信息系统,并定义了几种优势关系;文献[9]针对条件属性和决策属性都为区间数的多属性决策问题,定义了三种优势关系;文献[10]研究了不完备区间信息上基于优势关系的粗糙集方法;文献[11]针对前面定义的几种优势关系的不足,假定各属性都服从给定区间数上的均匀分布,提出了一种概率优势关系,但表达形式过于复杂,同时该假定也缺乏依据。考虑到区间数多属性决策中,通过可能度[12~13]能较好的表达区间数比较的优于程度,本文将可能度的概念引入到优势关系中,提出一种基于可能度的优势关系,通过对可能度α∈[0.5,1]的变化,来调节优势关系的“优于”程度,能较好的克服当前区间序信息系统上的几种优势关系的不足。
2 问题提出
2.1 区间序信息系统
定义1[8]区间值信息系统是一个四元组S=(U,A,V,f),其中,U= {x1,x2,…,xn}为对象的非空有限集合,A为非空属性集合;V=∪a∈AVa,Va为属性a的值域,f:U×A→V为一信息函数,表示对每一个a∈A,x∈U,f(x,a)∈Va,其中,Va是一个区间数,定义如下
f(x,a)=[aL(x),aU(x)]={p|aL(x)≤p≤aU(x),aL(x),aU(x)∈R}
表示在属性a下对象x的区间值。特别的aL(x)=aU(x)时,f(x,a)退化为一个实数。因此单值信息系统是区间值信息系统的特殊形式。
定义2[8]对区间值信息系统S=(U,A,V,f),若所有属性都具有优势关系,则称之为区间序信息系统。
2.2 区间序优势关系
定义3设区间序系统S=(U,A,V,f),B⊆A,几种优势关系定义如下[8~11]:
1)上优势关系:

对定义3的几种优势关系进行分析,可以发现这几种优势关系存在入一定的缺陷,具体如下:
1)下上优势关系的定义则过于严格。如[4.9,100]和[2,5],不满足下上优势关系,但实际上可认为[4.9,100]应优于[2,5]。
2)上下优势关系的定义过于宽松。根据上下优势关系,[2,3[2.999,100],同时又有[2.999,100[2,3],这也不合理,将会使得信息系统知识获取中出现误分类的问题。
3)上优势关系和下优势关系的定义则介于前两者之间,但仍会产生不合理结果。如根据上优势关系,[1,3[2.98,2.99],这不符合事实。同理,根据下优势关系,[2,[1.999,100],这也不符合事实。
4)上上下下优势关系为同时满足上优势和下优势关系的特例,但难以实现部分区间数的比较,从而导致分类的遗漏。如[1,2]和[0.9,10]无法比较,而[0.9,10]应优于[1,2]。
因此,有必要引入一种新的区间序信息系统的优势关系。
3 基于可能度的优势关系
3.1 可能度
为了比较区间数的大小,文献[13]定义了可能度的概念。
定义4当a,b同为区间数或有一个区间数时,设a=[aL,aU],b=[bL,bU],且记la=aU-aL,lb=bU-bL,则称
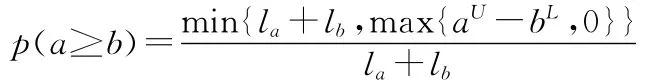
为a≥b的可能度。
可能度反映了区间数a≥b的可能性。通过可能度,能够实现任何两个区间数进行比较。因此,可将其引入到区间序信息系统中去。
对区间信息系统S=(U,A,V,f),对任意xi,xj∈U,a∈A,f(xi,a)=[aL(xi),aU(xi)],f(xj,a)=[aL(xj),aU(xj)],令=aU(xi)-aL(xi),=aU(xj)-aL(xj)。若f(xi,a)和f(xj,a)不同为实数,则
>>
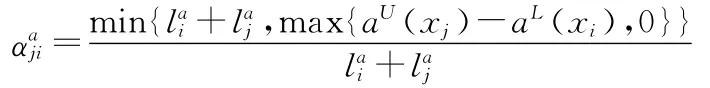
>
若f(xi,a)和f(xj,a)同为实数,则
>
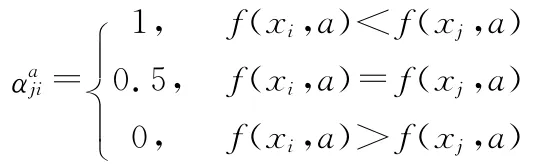
>
>
1)若=0,当且仅当aU(xj)≤aL(xi),即f(xj,a)≤f(xi,a)肯定成立。
>
>
3)若0<<1,则f(xi,a)与f(xj,a)相交或包含。
>
特别的,f(xi,a)=f(xj,a)时=0.5。即两个区间数相等时,一个数优于另外一个数的可能度为0.5。
>
3.2 α-可能度优势关系
定义5设区间值信息系统S=(U,A,V,f),B⊆A,给定可能度α∈(0,1],则可定义α-可能度优势关系和α-优势类:
>
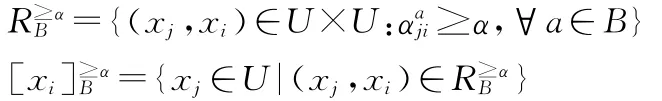
>
在区间序信息系统中引入可能度α后,可以通过阈值α∈(0,1]的调节来改变满足优势关系的可能程度,这样就提高了信息处理的灵活性。
>
定理1给定区间序信息系统S=(U,A,V,f),B⊆A,
>
1)若α∈(0,0.5],则是自反的,但不是传递的和对称的;
>
2)若α∈[0.5,1],则是传递的,但不是自反的和对称的。
自然灾害与气象问题对桥梁工程施工有着直接影响,火灾与爆炸这些安全事故受到工程施工现场环境的影响。针对这些工程环境风险,施工企业可以利用购买工程施工保险的方法转移风险。有意识地将风险与施工企业的经济效益联系在一起,在安全事故发生后,尽最大可能降低施工企业的损失。另外,要在施工过程中对一切安全因素进行有效监控,24小时监控施工现场的火灾发生影响因素与爆炸影响因素。安排专人负责工程环境风险管理,加强施工现场的监督力度,用规范的施工操作,预防工程环境事故的发生。
>
证明:(1)由α∈(0,0.5],则=0.5≥α,∀a∈B,则(xi,xi)∈,故是自反的。同时可以验证不满足自反性和对称性。
>
(2)由可能度的定义可知,α≥0.5时,对xi,xj,xk∈U,a∈B,若≥α≥α,则≥α,则可证明是传递的。同时可以验证不满足自反性和对称性。
>
不失一般性,和有以下性质:
>
定理2给定区间序信息系统S=(U,A,V,f),B⊆A,则
>
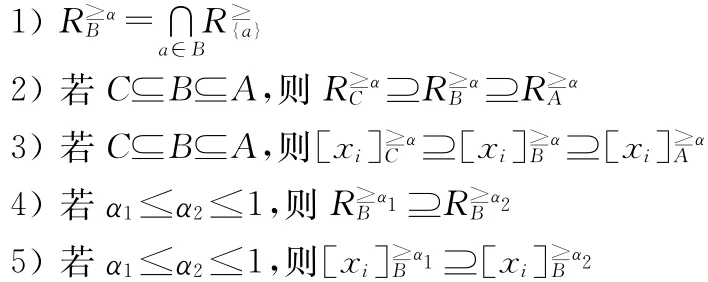
>
证明:1)~3)可由优势关系和优势类的定义直接证明。
>
4)由定义,={(xi,xj)∈U×U≥α2,∀a∈B},即对任意(xi,xj)∈,有≥α2,∀a∈B。由题设条件α1≤α2,则≥α2≥α1,∀a∈B,即(xi,xj)∈,由于(xi,xj)是任意的,则⊇。
>
5)由4)和α-优势类的定义可直接得到。
>
若在属性a下对象xj优于xi,则≥。有互补性知,≥0.5。由于α表示对象“优于”的最小可能程度,为保证分类的合理性,应取α∈[0.5,1]。
4 可能度优势关系下的粗糙近似
定义6设区间序信息系统S=(U,A,V,f),对给定的α∈[0.5,1],对任意B⊆A,X⊆U,上下近似定义如下:
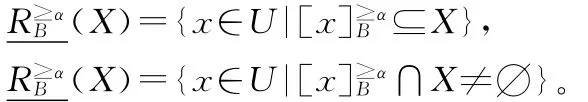
由定义6,能得到如下性质。
定理3区间序信息系统S=(U,A,V,f),B⊆A,α∈[0.5,1],则
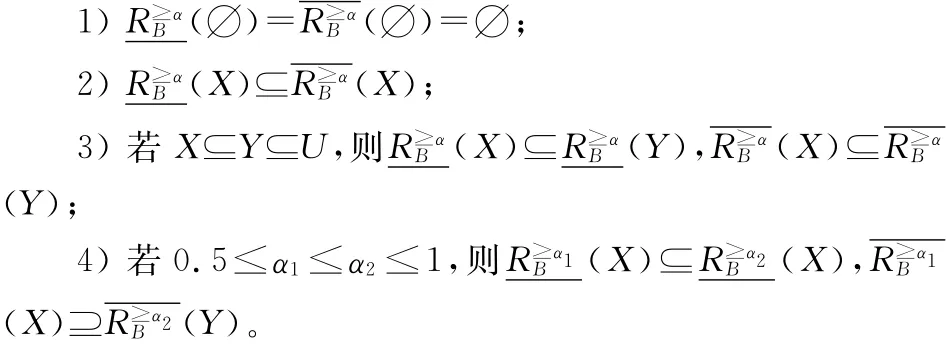
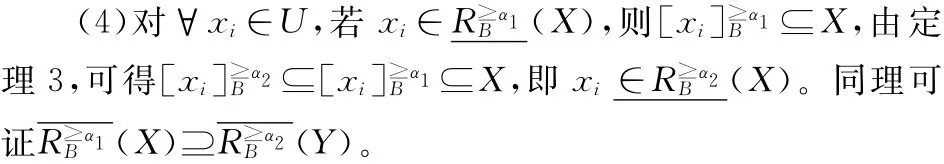
证明:1)、2)、3)可由定义直接证明。
5 算例
设有区间序信息系统S=(U,A,V,f),其中对象集U={x1,x2,…,x8},属性集A={a1,a2,a3,a4,a5,a6},所有属性均为效益型属性。区间序信息表如表1所示。
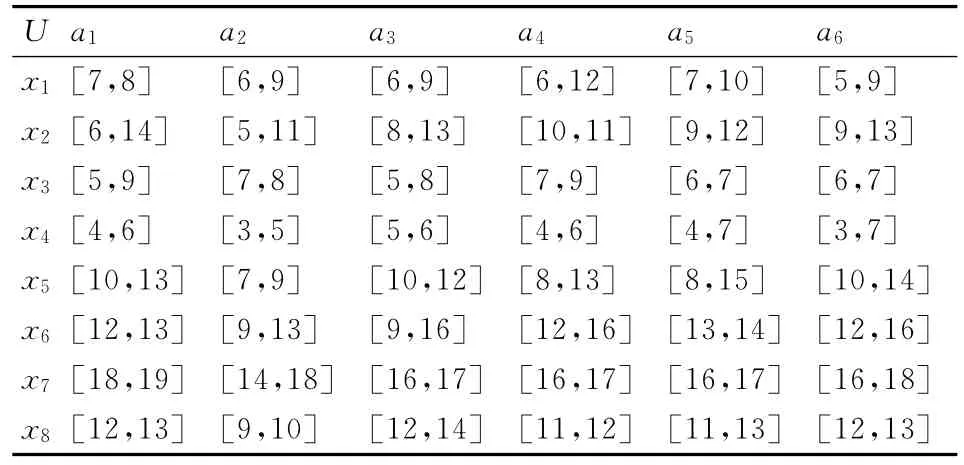
表1 区间序信息表
利用2.2节中五种优势关系对表1数据进行分类。由分类结果可知,下上优势关系虽然得到的分类准确性高,但过于严格,使得分类中含有的信息过少。如对象x1与x8,f(x1,a4)=[6,12],f(x8,a4)=[11,12],计算在a4下x8优于x1的可能度=0.857,即x8应划分到x1的优势类。但由下上优势关系,x8不能分到x1的优势类。而α-可能度优势关系而上下优势关系的定义过于宽松,虽然得到的分类信息量多,但容易引入不合理的信息。如对f(x1,a5)=[7,10],f(x2,a5)=[9,12],计算在a5下x2优于x1的可能度=0.833,即x2优于x1的概率大。而利用上下优势关系x1优于x2,这显然不合理。上优势关系和下优势关系的定义则介于前两者之间,但仍会产生不合理结果,同时也会遗漏部分有用信息。上上下下优势关系为同时满足上优势和下优势关系的特例,但难以实现部分区间数的比较,从而导致遗漏的问题。如对象x2和x6,由于f(x2,a1)=[6,14],f(x6,a1)=[12,13],采用上上下下优势关系则无法比较。计算在a1下x6优于x2的可能度=0.778,即x6优于x2的概率大。由α-可能度优势关系可知,x6优于x2,即上上下下优势关系产生了漏分的问题。
从上面分析可以看出,以往的五种优势关系的缺点在于没有对“优于”的程度进行合理的定义,从而造成分类中出现不合理或则遗漏信息的现象。下面采用本文提出的α-可能度优势关系进行计算,分别令α=0.5,0.6,计算结果如下
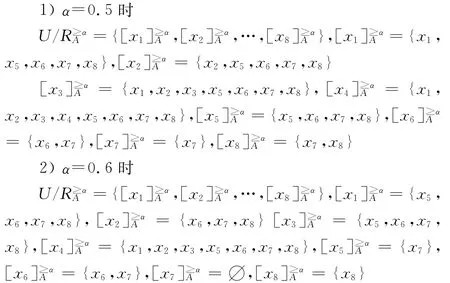
由计算结果可看出,α-可能度优势关系能够通过对α的变化来调节“优于”的宽松程度,这样就可以避免分类过宽和过窄而带来的不合理性。同时通过定义的α-可能度能够实现任意两个区间数的比较,这也避免分类中遗漏的问题。
6 结语
基于优势关系的粗糙集方法为多属性决策提供了一种新的思路。在现实世界中,由于决策问题的复杂性和不确定性,属性值难以直接用精确数来描述,而往往采用区间数的形式来表示。区间序信息系统是单值信息系统的扩展,针对区间序信息系统上的优势关系的研究对决策分析具有极其重要的意义。本文总结如下:
1)当前区间序信息系统上的几种优势关系存在着过宽或过窄的问题,从而导致分类出现不合理或遗漏的现象。针对这一问题,本文可能度的概念引入到优势关系中,提出了一种新的优势关系—α-可能度优势关系,进而研究了α-可能度优势关系的基本性质以及与其他优势关系的联系,并定义了基于α-可能度优势关系的粗糙集模型。通过对可能度α∈[0.5,1]的变化,来调节优势关系的“优于”程度,能较好的克服这些不足。
2)α表示一个对象优于另一对象的最小可能程度,能够反映决策者主观愿望,因此,可由决策者直接给定。
[1]Pawlak Z.Rough set[J].International Journal of Computer and Information Sciences,1982,11(5):341-356.
[2]H.L.Li,M.H.Chen.Induction of multiple criteria optimal classification rules for biological and medical data[J].Computers in Biology and Medicine,2008,38:42-52.
[3]J.F.Liu,Q.H.Hu,D.R.Yu.A weighted rough set based method developed for class imbalance learning[J].Information Sciences,2008,178:1235-1256.
[4]L.X.Shen,H.T.Loh.Applying rough sets to market timing decisions[J].Decision Support Systems,2004,37:583-597.
[5]S.Greco,B.Matarazzo,R.Slowinski.A new rough set approach to multicriteria and multiattribute classification[J].Lecture Notes in Artificial Intelligence,1998,1424:6067.
[6]S.Greco,B.Matarazzo,R.Slowinski,Rough sets theory for multicriteria decision analysis[J].European Journal of Operational Research,2001,129:147.
[7]S.Greco,B.Matarazzo,R.Slowinski,Rough sets methodology for sorting problems in presence of multiple attributes and criteria[J].European Journal of Operational Research,2002,138:247-259.
[8]QIAN Yuhua,LIANG Jiye,DANG Chuangyin.Interval ordered information systems[J].Computers and Mathematics with Applications,2008,56(8):1994-2009.
[9]DEMBCZYNSKI K,GRECO S,SLOWINSKI R.Rough set approach to multiple criteria classification with imprecise evalu-ations and assignments [J].European Journal of Operational Research,2009,198(2):626-636.
[10]YANG X B,YU D J,YANG J Y,et al.Dominance-based Rough se t approach to incomplete interval-valued information system [J].Data & Knowledge Engineering,2009,68(11):1331-1347.
[11]杨青山,王国胤,张清华,等.基于优势关系的区间值粗糙集扩充模型[J].山东大学学报(理学版),2010,45(9):7-13.
[12]沈丽容,黄洪.基于贝叶斯和可信度的糖尿病诊疗系统研究[J].计算机与数字工程,2011(11).
[13]Nakahara Y.User oriented ranking criteria and its application to fuzzy mathematical programming problems[J].Fuzzy Sets and Systems,1998,94:275-286.
[14]Nakahara Y,SaSakiM,Gen M.on the linear programming problems with interval coefficients[J].International Journal of Computer Industrial Engineering,1992,23:301-304.
