感应线圈电路分析＊

杨立志 周穗华 陈志毅

（海军工程大学兵器工程系 武汉 430033）

1 引言

使用导线绕制的感应线圈，不仅有直流电阻，它还是一个电感元件，另外，导线的匝与匝之间、层与层之间有分布电容［1］的存在。感应线圈是一个由电阻、电感、分布电容构成的串联谐振电路，其等效电路［2］如图1所示。从图中可以看出：实际检测到的信号并不是感应电动势，它实际上是感应电动势经过一个传递函数后的电压。

2 感应线圈工作状态分析

2.1 零输入响应

当通过感应线圈的磁通发生变化时，感应线圈才能产生感应电动势［3］，在无磁空间或者静磁场，感应线圈是没有感应电动势的，而此时感应线圈的等效电路［4］如图2所示。

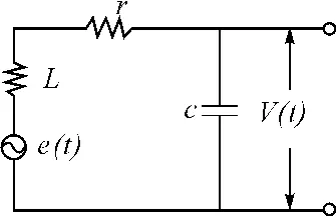
图1 感应线圈的等效电路

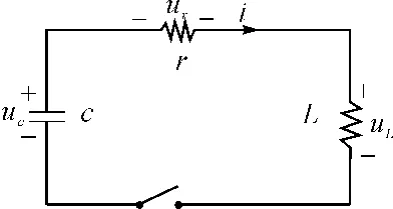
图2 感应线圈等效电路

这是一个二阶电路，假设电路有初始状态，电容两端电压为u0。当开关闭合后，此电路的放电过程其实就是二阶电路的零输入响应。在如上图所示，指定的电压、电流参考方向，根据基尔霍夫定律［5］可得：

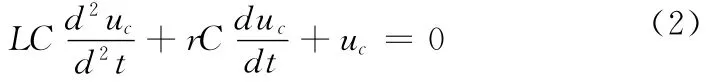
不妨设uc＝AeSt，其相应的特征方程为

通过解特征方程得：

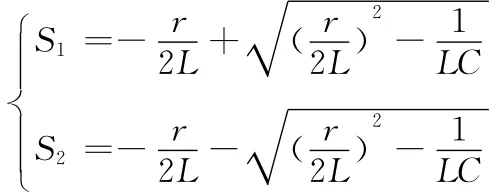
由上式可见，特征方程的根与元器件的初始储能没有关系，只和电路的参数和结构有关系。根据给定的初始条件，可得电容两端电压为

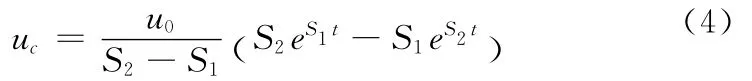
由于电路中r、L、C的参数不同，特征根有三种情况：两个不等的实根、一对相等的实根、一对共轭复根。

1）当r≥2时：

特征方程的特征根有两个不相等的实根，电容上的电压为

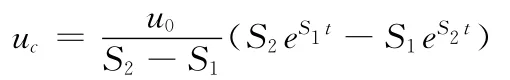
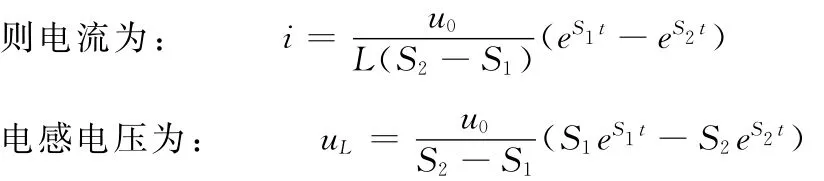
把uc、i和uL，分别除以u0归一化，利用Matlab仿真计算，可以得到它们随时间变化的趋势。

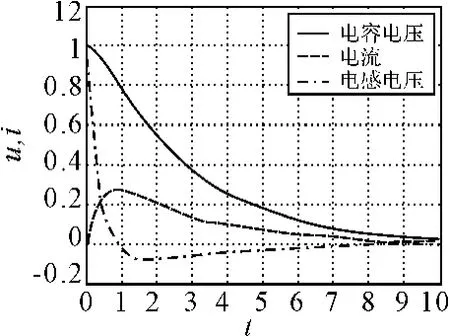
图3 uc、i和uL随时间变化的曲线

如图3所示，电容两端电压一直在减小，说明电容一直处于放电过程；电流先增大，随着电容两端的电压的减小到一定数值，电流开始减小，但是电流方向始终没有改变；电感在电流达到最大以前吸收能量，当电流过了最大值以后，电感开始释放能量。所以，当r≥2时，等效电路是一个非振荡电路［6］。

2）当r＜2时；

特征方程的特征根S1和S2是一对共轭复根。

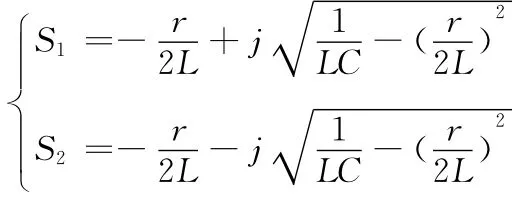
电容上的电压为

电流为

电感电压为

把uc、i和uL，归一化，利用 Matlab仿真计算，可以得到它们随时间变化的趋势。

图4 uc、i和uL随时间变化的曲线

如图4所示，电容电压先变小，电压变为零后，反向增大，然后再变小；电路中的电流先增大，再变小，电流变为零后，反向增大，然后再变小；电感电压的变化趋势和电容电压相似，只是变化趋势滞后与电容电压。电容电压、电流、电感电压将周期性的改变方向，它们的波形呈现衰减振荡的状态。所以，当r＜2时，等效电路是一个振荡电路。

为了使感应线圈对于外界的信号有一个良好的响应，感应线圈的等效电路应该是一个非振荡［7］的电路。要使等效电路是一个非振荡的电路，必须调整电阻、电感和电容的数值，使其满足r≥2。改变感应线圈的参数，就可以改变电阻、电感和电容的数值，电感主要由感应线圈的匝数决定，导线的线径会影响电阻和电容，导线材料的电阻率也直接决定电阻的大小。通过理论计算和实验验证，来合理搭配感应线圈参数，使电阻、电感和电容满足条件r≥2，从而使得感应线圈能够对信号有一个良好的响应。

2.2 正弦稳态响应

感应线圈在交变磁场中会产生感应电压，与静磁场或者无磁空间里的感应线圈的等效电路是不一样的［8］。在弱磁场中，感应线圈产生的感应电压比较小，必须加匹配电阻和后续的放大电路，才能满足通信的要求。当考虑匹配电阻和放大电路时，整个磁性天线的等效电路［9］如图5所示。

由图5可得：

图5 磁性天线等效电路

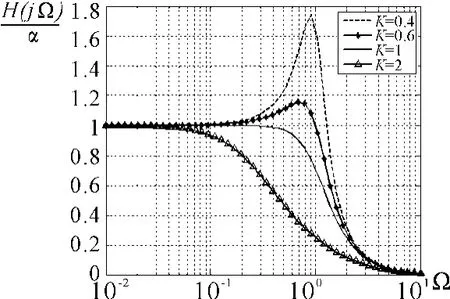
图6 磁性天线的幅频特性曲线

不同的K值，会使电路的幅频特性不同，如图6所示。K＞1时，磁性天线工作在过阻尼状态；K＜1时，磁性天线工作在欠阻尼状态。无论磁性天线工作在过阻尼状态还是欠阻尼状态，相对于输入信号来说发生了畸变。K＝1时，磁性天线工作在临界阻尼状态，对于输入信号在很宽的带宽内能够稳定的响应［12］。

3 工作状态调整

如图6所示，K＝0.4时，虽然峰值很高，但是峰很尖锐；K＝0.6时，峰值相对较小，但是峰值附近比较窄的带宽内幅值是相对平坦的。当磁性天线工作在欠阻尼状态时，频率系数Ω为1附近，幅值要比临界阻尼状态大；随着阻值系数K值的减小，幅值会增大，但是K值越小，幅频特性曲线越尖锐。

由阻值系数的定义式可知，阻值系数与匹配电阻成反比，所以，幅频特性曲线的峰值与匹配电阻成正比。对于单一频率通信或者比较窄带宽内的通信，可以通过调节匹配电阻，使阻尼系数小于1，让感应线圈工作在欠阻尼状态。这时，在感应线圈谐振频率点附近幅值较大，因此，在这一频段内进行通信时，会提高磁性天线的灵敏度。另外，调节匹配电阻，可以调整峰值附近曲线的平坦程度。

一个两万匝的感应线圈，实际测得的电感L为66.36H，谐振频率f为105Hz；其分布电容C可由公式：C＝1／（4π2f2L）得到，结果为31.58nF。感应线圈放置在磁场强度为B正弦变化的电磁场中，这个电磁场是由格拉斯磁环产生的。改变电磁场的频率f，感应线圈两端的感应电压V也发生变化。感应线圈的灵敏度定义为

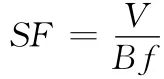
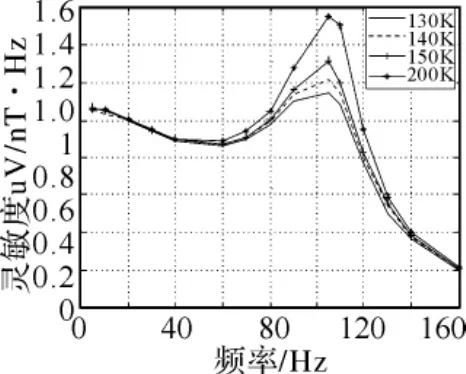
图7 感应线圈灵敏度曲线

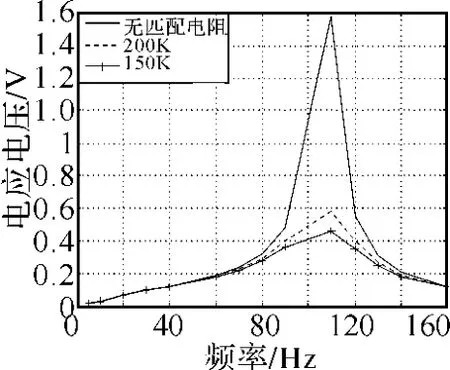
图8 感应线圈感应电压曲线

在感应线圈两端串联不同阻值的匹配电阻，测得几组数据，绘成曲线如图7、8所示。从图7、8中可以看出：1）当频率小于80Hz，大于120Hz时，四组试验的灵敏度、感应电压数值很接近，只有在谐振频率附近，它们的数值发生了很大变化；2）无匹配电阻时，谐振频率点处的数值与附近的值变化巨大；3）随着匹配电阻阻值的减小，灵敏度、感应电压曲线的峰值在减小。这说明，改变匹配电阻的大小，只对谐振点附近的幅值产生很大的影响，对其他频率段影响较小；感应线圈不进行电阻匹配，不能利用谐振点附近的频带进行通信；适当的匹配电阻，会使感应线圈在谐振频率附近比较窄的带宽内，对外界电磁场稳定响应，感应线圈在此处不能稳定的响应。

4 结语

当需要很大带宽时，感应线圈谐振频率应当很大，并且可以调整匹配电阻使其工作在临界阻尼状态；当需要带宽较窄时，可以利用谐振频率附近灵敏度较高的频带。在谐振频率附近时，需要选择合适的匹配电阻，才能使感应线圈对信号稳定的响应。

［1］王言章.混场源电磁探测关键技术研究［D］.吉林大学.

［2］C.Coillot，J.Moutoussamy，P.Leroy，G.Chanteur，A.Roux.Improvements on the design of search coil magnetometer for space experiments［J］.Sensor Letters，2007（5）：167－170.

［3］蒋安林.超长波水下磁性天线小型化研究 ［D］.海军工程大学，2011.

［4］梁岩冰.TEM接收线圈的测试分析［D］.吉林大学.

［5］康华光，陈大钦.电子技术基础［M］.华中理工大学.

［6］邱关源.电路［M］.北京：高等教育出版社，1999.

［7］巨汉基，朱万华，方广有.磁性感应线圈传感器综述［J］.地球物理学进展，2010.

［8］James E.Lenz.A Review of Magnetic sensors［J］.Proceeding of the IEEE，1990.

［9］Jones DL，Burke.ELF Radio［C］.London：IEE 100Years of radio conference Publicstion，1995.

［10］彭伟.铂电阻测温系统数值计算软件设计研究与实现［J］.计算机与数字工程，2012（5）.

［11］汪小亮，姚旺生.基于蚁群算法的时序电路测试生成研究［J］.计算机与数字工程，2011（10）.

［12］邵英秋.感应式磁传感器线圈参数及其接口电路的研究［D］.长春：吉林大学，2008.