三次抛物线形渠道断面收缩水深的简化计算公式

王志云 滕 凯

（1.齐齐哈尔市水利工程质量与安全监督站，黑龙江齐齐哈尔 161006；2.齐齐哈尔市水务局，黑龙江齐齐哈尔 161006）

由于抛物线形断面具有良好的水流条件及力学性能，因此在城市供排水及水利水电工程中，工程设计部门常根据输水流量及地质条件，将渠道断面设计为半立方抛物线、二次抛物线或三次抛物线形式之一，因此相关抛物线形式的水力计算问题也逐渐引起了有关学者的重视[1～5]，其中关于半立方抛物线及二次抛物线形渠道断面收缩水深的计算已有相关研究成果[6～9]，而三次抛物线形断面渠道收缩水深的计算研究则相对较少。

文献[10]针对三次抛物线形渠道断面收缩水深计算涉及高次方程的求解问题，弃用常规的计算过程繁复且成果精度不高的试算法及图解法，从三次抛物线形断面渠道收缩水深的基本方程入手，通过对初始迭代值的优化拟合，获得了可直接完成求解的近似计算公式，具有一定的实际意义。但因该公式需分别完成中间参数及初值计算，求解过程仍显繁琐。

为了进一步简化三次抛物线形断面收缩水深的计算过程，本文采用优化拟合的方法，以标准剩余差最小为目标函数，获得了一种表达式较为简捷、计算精度较高的近似公式。

1 收缩水深的基本计算公式

收缩水深的基本方程为[11]：

式中：E0为以收缩断面底部为基准面的过水建筑物上游总水头，m；hc为收缩断面处的水深，m；Q为过水流量，m3/s；g为重力加速度，m/s2；φ为流速系数；Ac为三次抛物线形断面面积，m2。

三次抛物线形断面的曲线方程为：

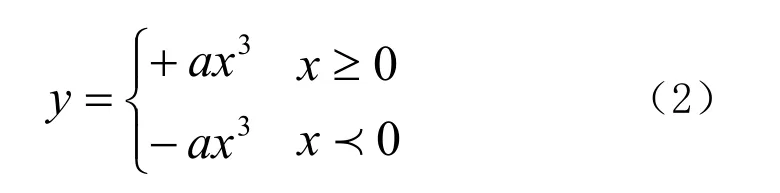
其过水断面面积为：

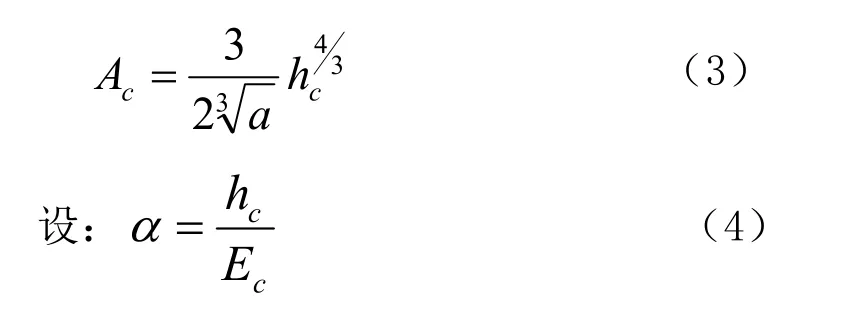
将式（3）、（4）代人式（1），并设：

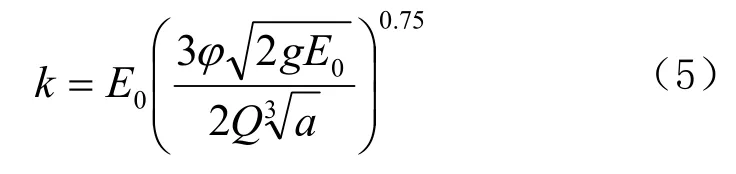
经整理即可获得计算三次抛物线形断面收缩水深的计算公式为：

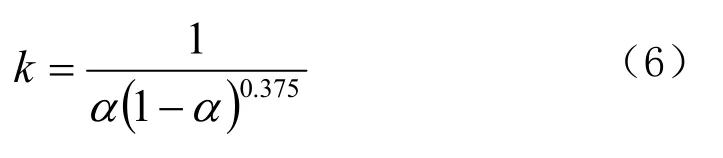
2 近似计算公式的建立及精度分析

2.1 公式建立

式（6）为高次函数的超越方程，无法直接获解。为避免利用式（6）的超越方程求解问题，现通过以下方法寻求其替代函数：

(1) 根据式（6）函数，展绘α～k关系曲线。

(2) 经对α～k关系曲线的线形分析，初步拟定以下函数为备选替代函数。

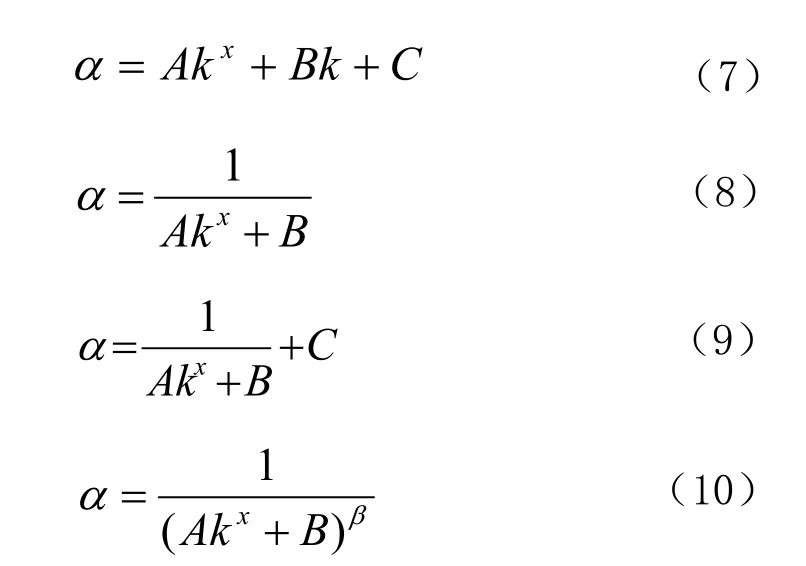
式中：A、B、C、x、β分别为待定系数及指数。

(3) 在工程实用范围内[10]（即 0.01≤α≤0.5），采用优化拟合的方法，以标准剩余差最小为目标函数[12]即：

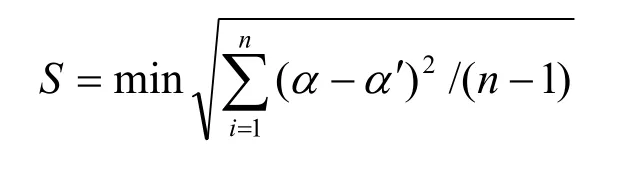
经对式（7）～（10）逐次逼近拟合[13]可知，式（10）的标准剩余差S最小，其替代函数式为

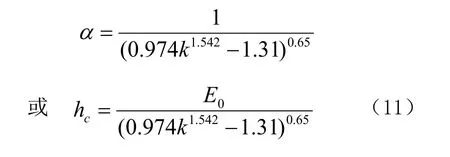
2.2 精度分析及比较

为比较式（11）与式（6）的拟合精度，考虑在工程实用范围内（即 0.01≤α≤0.5， 2.59≤k≤100.38），取不同的iα值即可由式（6）分别计算出与之相对应的ki，再将ki代入式（11）求得与之相对应的αi′，并由下式完成式（11）替代式（6）的拟合相对误差，结果见表1。

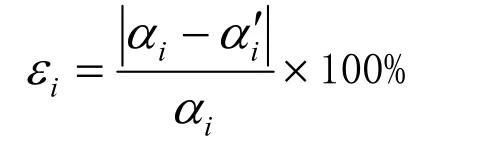
表1 式（11）替代式（6）误差计算结果

由表1可见，在工程实用范围内。

用式（11）替代式（6）的最大拟合相对误差：

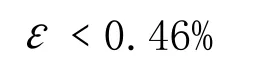
式（11）具有较好的拟合替代精度。

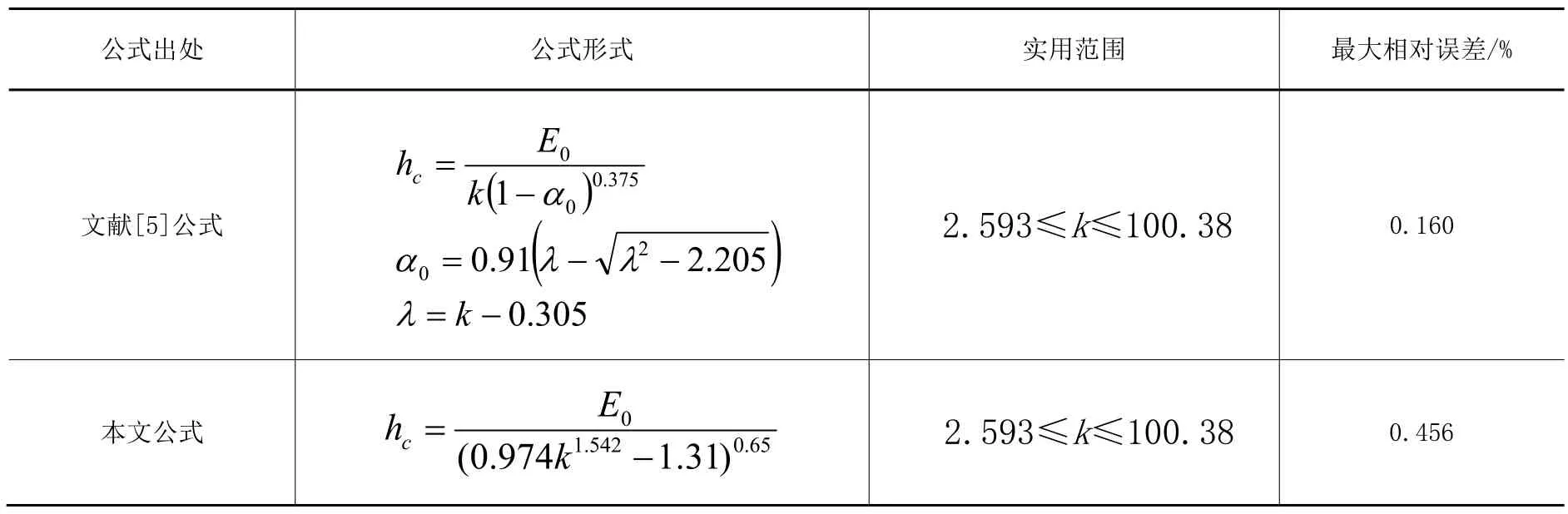
表2 抛物线均匀流水深公式形式、最大相对误差比较

通过对公式形式比较可见，本文公式较文献[5]公式更加简单，计算过程也更加简捷。具体比较结果见表2所示。

3 应用举例

选文献[5]计算实例：已知闸前断面总水头E0=15m，通过流量Q =162 m3/s，流速系数φ=0.95，若采用三次抛物线形断面渠道，其断面曲线方程为

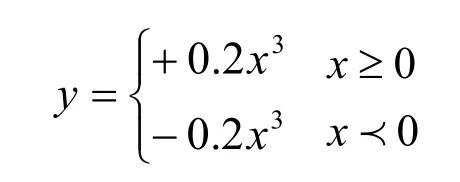
求闸后断面收缩水深hc。

将已知参数代人式（5）可求得

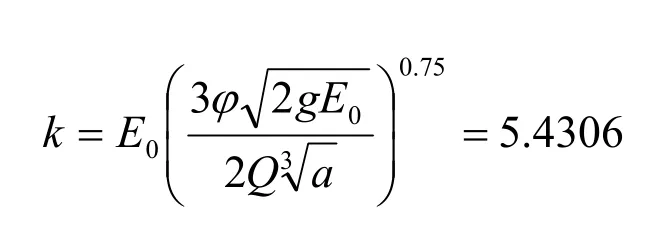
将k =5.4306代人式（11）即可求得

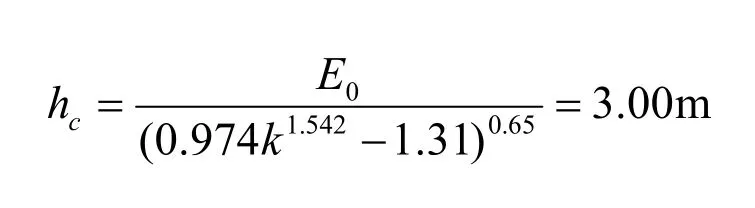
本例收缩水深的精确解为hc=3.00m，本文公式计算成果的相对误差为0。

4 结 语

通过优化拟合的方法完成了对三次抛物线形渠道断面收缩水深计算公式的拟合，获得了表达形式简单、求解精度较高的计算公式，经误差分析及实例计算表明，在工程实用范围内，本文公式的最大相对误差为0.46% 。

[1]魏文礼,杨国丽.立方抛物线渠道水力最优断面的计算[J].武汉大学学报：工学版,2006,(3)∶49-51

[2]张志昌,刘亚菲,刘松舰.抛物线形渠道水力最优断面的计算[J].西安理工大学学报,2002,18（3）：235-237

[3]明万才,黄开路,张晓莲.立方抛物线形断面明渠水力计算探讨[J].水利科技与经济,2002,8（2）：74

[4]文辉,李凤玲.立方抛物线形渠道水力计算的显式计算式[J].人民黄河,2010，（1）：75-76

[5]赵延风,王中正,方兴等.半立方抛物线形渠道正常水深算法[J].排灌机械工程学报,2011,2（3）：241-245

[6]文辉,李风玲.立方抛物线断面渠道收缩水深的直接计算方法[J].人民长江,2009,40（13）：58-59

[7]文辉,李风玲.抛物线形断面渠道收缩水深的解析解[J].长江科学院院报,2009,26（9）：32-33

[8]芦琴,王正中,任武刚.抛物线形渠道收缩水深简捷计算公式[J].干旱地区农业研究,2007,25（2）∶134-136

[9]赵延风,宋松柏,孟秦倩.抛物线形断面渠道收缩水深的直接计算方法[J].水利水电技术,2008,39（3）∶36-37

[10]冷畅俭，王中正.三次抛物线形渠道断面收缩水深的计算公式[J].长江科学院院报,2011,28（4）∶29-31,35

[11]清华大学主编.水力学（修订本）上册[M].北京∶清华大学出版社,1990

[12]王慧文.偏最小二乘回归法及其应用[M].北京国防工业出版社,1999

[13]阎凤文.测量数据处理方法[M].原子能出版社,1988