运动平台磁体感应磁场建模研究*
2012-07-11孙宝全林春生
张 宁 孙宝全 林春生
(海军工程大学兵器工程系 武汉 430033)
1 引言
运动平台磁性壳体及电磁设备所产生的磁场对平台搭载的磁场测量系统造成严重的干扰。为了有效地降低磁场干扰,为搭载的磁场测量系统创造良好的工作环境,需要对运动平台的磁干扰的特性及数学模型进行研究。
运动平台的磁场可分为固有磁场和动态磁场[1~3]。固有磁场是运动平台在地磁场长期磁化所形成的,其大小比较稳定。可以通过屏蔽或退磁的手段进行处理。运动平台的动态磁场包括地磁场磁化产生的感应磁场以及高速运动时产生的涡流磁场。涡流磁场是由于通过运动平台壳体的磁通发生变化而引起的,因此它与平台的运动速度、姿态、地磁矢量以及壳体的形状有关,一般产生的干扰较小。
感应磁场起源于运动平台内部的铁磁性材料在地磁场中运动,是铁磁性材料在地磁场中磁化形成的。铁磁性物体位于运动平台内,主要是舱内的各种电气设备和一些小型结构件,当背景磁场的大小或方向变化时,感应磁场也会随之变化。铁磁性材料的磁性参数差别很大,磁化特性差别很大,不同的磁性材料具有形状迥异的磁滞回线,目前还没有普适的分析方法与数学模型。
当这些铁磁性材料离磁场测量设备安装点较远,可以近似等效成一个或多个位于中轴线附近的磁偶极子[4~5]。本文就建立运动平台磁体感应磁场的磁偶极子模型进行研究,并对模型进行有效性验证。
2 感应磁场的磁偶极子模型
工程应用时,如果远场条件满足,则可采用磁偶极子模型对磁体的空间磁场进行描述。
在如图1所示的直角坐标系下,磁偶极子的磁位表达式为

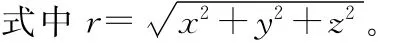
对式(1)求偏导可得磁偶极子模型的公式
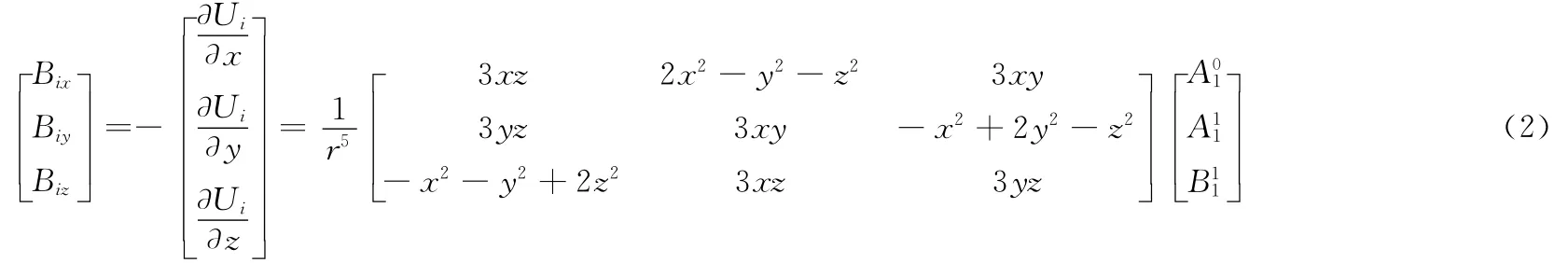
确定出系数A01、A11和B11,即可计算出空间任意点(远场区内)的磁场矢量。
在运动平台载体坐标系下,假定磁体所在的背景磁场矢量为
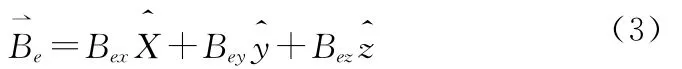

图1 磁体在背景磁场作用下感应磁场的示意图
该背景磁场矢量作用下的感应磁场可等效为背景磁场三分量Bex、Bey和Bez分别作用下感应磁场的矢量叠加。以Bex分量为例,如图1所示,磁体内部的感应磁场Mix沿x轴方向,且
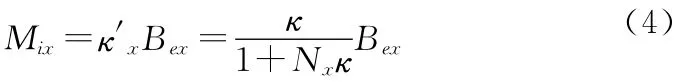
式中κ′x为磁体x轴方向的视磁化率,κ为材料真磁化率,Nx为磁体x轴方向的消磁系数(退磁系数)。
由磁偶极子模型可得

式中~κ′xBex,记作=mxBex。当测量点在载体坐标下确定后,式(5)中的矩阵也随之确定,式(5)可写成
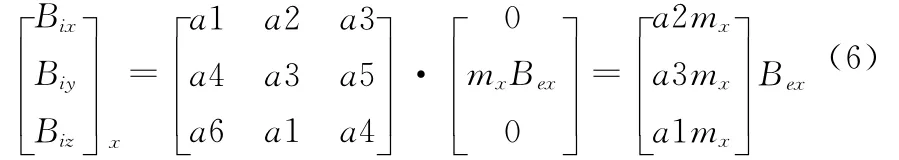
同理,对于背景磁场矢量,有
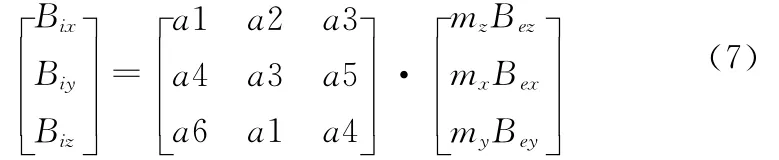
由上分析可知,背景磁场矢量作用下,磁体的感应磁场在远场区可用磁偶极子模型进行描述,模型中的系数、和分别为mzBez、mxBex和myBey。当背景磁场矢量(即Bex、Bey和Bez)变化时,磁偶极子描述的感应磁场也将随之变化。由于磁体形状的关系,一般的mx≠my≠mz,故磁体内部的感应磁场与背景磁场不同向,两者具有一定的夹角。
已知背景磁场矢量,若考虑x轴上的磁场,即y=0,z=0,则有

其它两轴的情况与此一致。按式(8)对磁场三分量进行计算,即可得出mx、my和mz,进而根据式(7)推算出不同背景磁场矢量下磁体磁偶极子场在远场区的空间分布。
3 模型系数的拟合计算与分析
以矩形磁体为例,用ANSYS软件得到感应磁场的数值计算数据对磁偶极子模型的系数进行拟合,以分析磁偶极子模型描述磁体远场区磁场的有效性。矩形磁体的参数:尺寸为2×3×1,相对磁导率为100(由于材料结构的消磁效应,增大磁导率对计算结果的影响不大)。为研究方便作四点假设:1)铁磁性材料磁各向同性;2)铁磁性材料未发生磁饱和(地磁场为弱磁场[6~7]),且工作在磁滞回线的线性区;3)铁磁性结构产生的感应磁场可线性叠加;4)只考虑铁磁性结构的感应磁场。通过建立亥姆霍兹线圈组计算模型产生三维变化的背景磁场,背景磁场三分量分别取Bex=50000nT、Bey=90000nT和Bez=70000nT,在线圈组的公共区内,空间磁场比较均匀[8~10],可用来作为磁体的背景磁场。
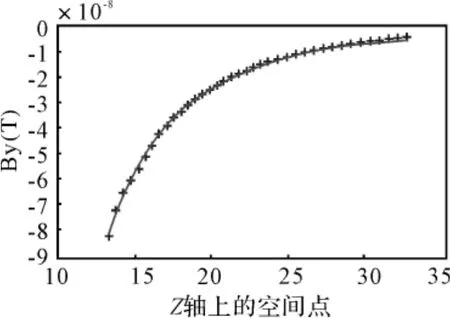
图2 Z轴上磁场分量By的计算结果及其拟合曲线
图2所示为Z轴上磁场分量By计算结果的拟合曲线,“+”线是计算结果,红色实线是拟合曲线,拟合效果较好,得到系数my。表1为解算得到的三组模型系数。

表1 解算得到的三组模型系数
4 模型误差分析及验证
模型误差的计算公式为
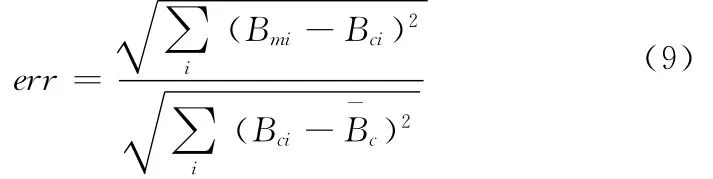
式中Bmi表示模型推算的第i个空间点的磁场值,Bci表示有限元计算的第i个空间点的磁场值,对应点的空间坐标相同为计算的空间磁场的平均值。计算结果表明,当空间点与磁体干扰源的距离大于干扰源尺度的3~4倍时,即可认为该点位于远场区。由于存在背景磁场,Bci为两次数值计算的差值,第一次有限元计算模型中不加磁体,计算所得的是背景磁场的空间分布;第二次在模型中加入磁体,计算所得的是背景磁场与感应磁场空间分布的叠加。
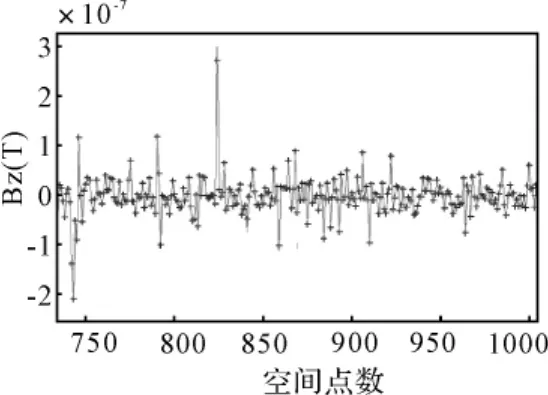
图3 远场区磁场分量Bz的计算结果及其模型推算曲线
磁偶极子模型推算远场区空间点磁场的效果如图3所示,“+”线是计算结果,实线是模型推算曲线,两者一致度很好,说明了磁偶极子模型描述磁体远场区磁场的有效性。
通过改变加载电流将背景磁场三分量分别变为Bex=80000nT、Bey=30000nT和Bez=40000nT,利用有限元计算出该磁场背景下的磁场空间分布,同时利用表1中的模型系数进行模型推算,效果如图4所示,“+”线是计算结果,浅绿色实线是模型推算曲线。
根据式(9),两次模型推算的误差如表2所列,基本都在10%左右,说明了磁偶极子模型的有效性,且利用一个背景磁场下的感应磁场数据可推算任意背景磁场下的感应磁场分布。
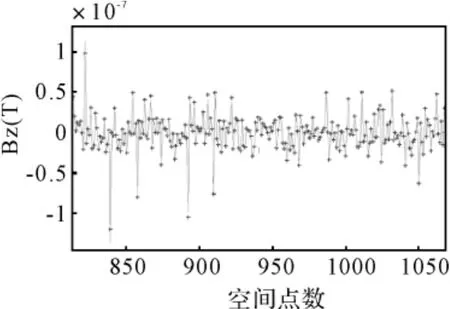
图4 另一组远场区磁场分量Bz的计算结果及其模型推算曲线

表2 磁偶极子模型的推算误差
5 结语
本文建立的磁偶极子模型可描述感应磁干扰的远场空间分布,模型误差约为10%,模型适用于单个磁体干扰源,当载体内包含多个磁体干扰源时,其感应磁场空间分布可看成多个磁偶极子模型的线性叠加,每个模型对应一个磁体。
[1]林春生,龚沈光.舰船物理场[M].北京:兵器工业出版社,2007:25-45.
[2]庞学亮,林春生,张宁.基于改进型偏最小二乘回归法导弹磁补偿研究[J].弹箭与制导学报,2009,29(5):49-52.
[3]庞学亮,林春生,张宁.飞机磁场模型系数的截断奇异值分解法估计[J].探测与控制学报,2009,31(5):48-51,68.
[4]张朝阳,肖昌汉,高俊吉,等.磁性物体磁偶极子模型适用性的试验研究[J].应用基础与工程科学学报,2010,18(5):862-868.
[5]杨云涛,石志勇,关贞珍,等.一种基于磁偶极子磁场分布理论的磁场干扰补偿方法[J].兵工学报,2008,29(12):1485-1491.
[6]赵晓伟.地磁场测量的研究[J].延安大学学报:自然科学版,2009,28(4):48-49,53.
[7]康伟芳,杨溢.用自旋阀巨磁电阻传感器测量地磁场[J].武汉理工大学学报:信息与管理工程版,2009,31(4):584-586,601.
[8]陈修芳.亥姆霍兹线圈磁场分布及其测量[J].大学物理实验,2009,22(3):33-36.
[9]杨能勋,薛琳娜.亥姆霍兹线圈磁场均匀性的研究[J].延安大学学报:自然科学版,2011,30(1):29-31.
[10]朱业俊,陶小平,孙腊珍.亥姆霍兹线圈磁场的探究[J].物理实验,2010,30(3):42-46.
