基于拓扑相似度的航迹关联算法＊

郭 强 符 拯

（1.海装西安局 西安 710054）（2.海军驻航天三院军事代表室 北京 100074）

1 引言

在多雷达跟踪系统中，融合来自多部雷达对同一目标的观测信息可以获得更为精确的目标状态估计。实际系统多采用分布式的融合体系结构，即单部雷达产生局部航迹传送到融合中心，在融合中心进行航迹关联；对同一目标的航迹进行融合，得到系统航迹。多目标环境中，航迹关联是多雷达数据融合中的一个关键问题，也是实现航迹融合的前提，关联判决结果将直接影响整个融合系统的性能［1～2］。系统中的多种不确定性，包括雷达自身的系统误差、随机误差以及密集的杂波干扰，是航迹关联实际应用中面临的主要问题。

用于航迹关联的算法通常可分为两类：一类是基于统计的方法，另一类是基于模糊数学的方法。统计方法的思想是将航迹关联问题转换为假设检验问题，构造利用两局部节点的航迹估计服从特定分布的检验统计量，并根据事先确定的门限值来判断两航迹是否来自同一目标。在文献［3］中，提出了一系列基于统计方法的航迹关联算法。模糊方法的思想是利用在航迹关联判决中存在的模糊性，用模糊数学的隶属度函数来表示，也就是用隶属度概念来描述两个航迹的相似程度。为此，文献［4］又研究了模糊航迹关联算法，讨论了多传感器航迹关联中模糊因素集与隶属度函数选择，研究模糊因素的确定与模糊权集的动态分配等问题。然而，当系统包含较大的导航、传感器校准及转换和延迟误差时，有时统计和模糊的方法均显得力不从心。

本文提出了一种新的航迹关联算法——拓扑相似法［5］，该算法充分利用目标之间的拓扑信息来衡量航迹间接近的程度，对样本量的大小没有太高的要求，分析时也不需要典型的分布规律，为航迹关联问题探索一条新的途径。

2 问题的描述

设目标状态矢量由目标的位置、目标的速度、目标航向以及目标加速度等p个特征参数构成。

为了讨论问题的方便，假设送至融合中心的所有状态估计＾Xij（i＝1，2，…M；j＝1，2，…ni）都在相同的坐标系里，并且各传感器同步采样，这里M是局部节点数，ni是节点i的航迹个数。对于特殊的应用可以定义需要的坐标转换和恰当的时间校正，另外，还假设数据的传输延迟时间为零。统一的坐标转换是容易实现的工作，时间延迟可以通过延迟修正和外推补偿，而采样与更新的不同步可通过平滑、插值及外推完成目标状态估计点的时间校准。为了进一步简化分析这里假定M＝2讨论。

设局部节点1、2的航迹号集合分别为

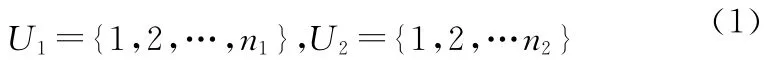
把来自局部节点2的n2条航迹看成是n2个已知模式，而把局部节点1的航迹i（i∈U1）看成是待识别模式，那么航迹关联问题实际上就是一个典型的模式识别问题。

3 拓扑相似法的原理

3.1 目标拓扑结构

受到人工判别过程的启发：将待关联目标周边的其他目标作为参照物，目标间的空间信息就可为关联判决提供更多的参考。定义这种新的信息称为目标的拓扑结构［6］，即以待判目标为原点，周边的目标作为参照物所构成的拓扑结构，空间上相距较近的目标，拓扑结构是截然不同的。因此，拓扑结构是区分目标的一个有效的特征。将不同雷达观测到的同一个目标的拓扑结构进行比较，实际上就是把雷达观测坐标进行了平移变换，把坐标原点平移到了待判决目标上。图1中显示了5个目标在空间的分布情况，图2（a）中比较了不同雷达对目标C观测的拓扑结构，方位偏差导致了拓扑结构之间的旋转，虽然观测的目标的绝对位置有较大差异，但拓扑结构的差别却不大；图2（b）是两部雷达看到的不同目标（B目标和C目标）的拓扑结构之间的比较，差异很大。

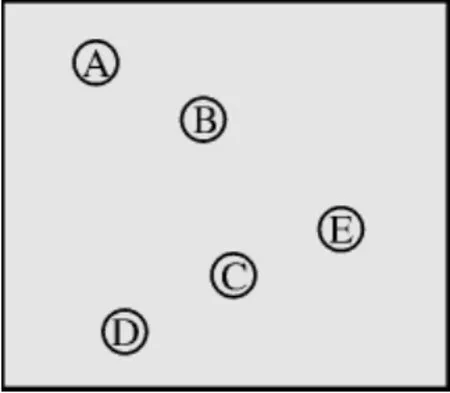
图1 目标空间分布

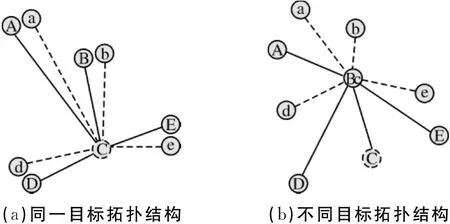
图2 拓扑结构

3.2 计算拓扑相似度

依据每个雷达在k时刻探测到的目标，以任一目标为参考点，其他目标到参考点的距离差向量为成员，可以计算出每个目标的拓扑。这个拓扑表示为一个向量序列，其中的每一个成员是邻居到该目标参考点的距离差向量，而且按方位角递增顺序排列［7］。

假设雷达监视区内有N个目标，则局部节点1的目标参考点t及其N－1个邻居的坐标向量序列是

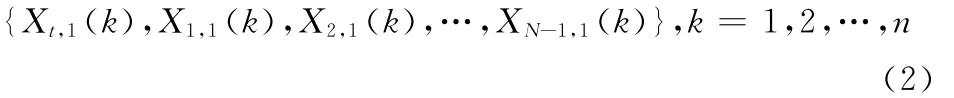
拓扑序列是

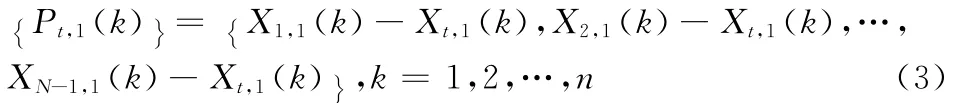
同理，局部节点2的目标参考点r及其N－1个邻居的坐标向量序列是

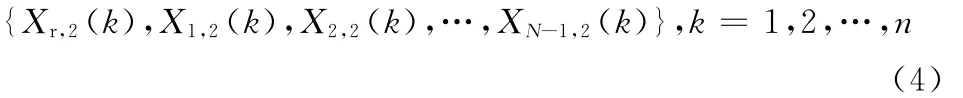
拓扑序列是

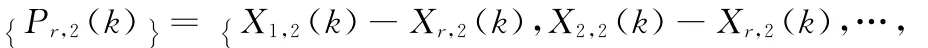
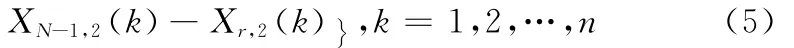
所以对局部节点1来说，目标到参考点的距离可以表示为

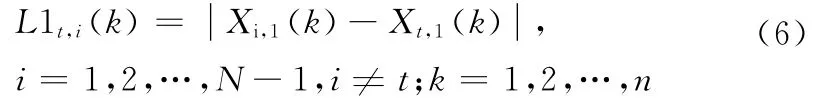
同理，对局部节点2来说，目标到参考点的距离可以表示为

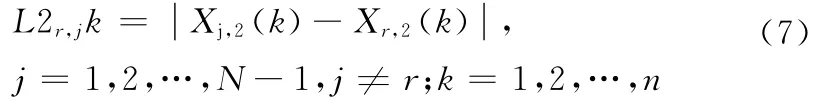
这样，航迹与航迹之间的相似程度用拓扑相似度来表示

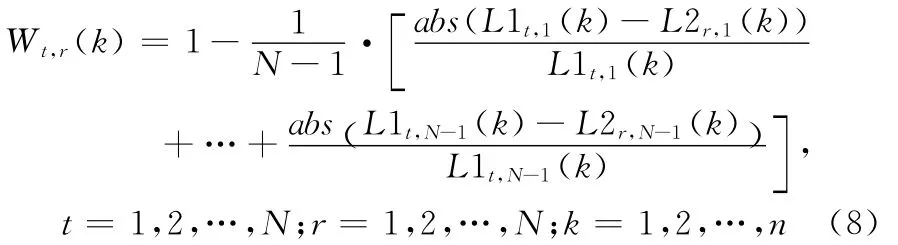
这里，abs为求绝对值运算，计算拓扑相似度的拓扑算子为St，r（k）

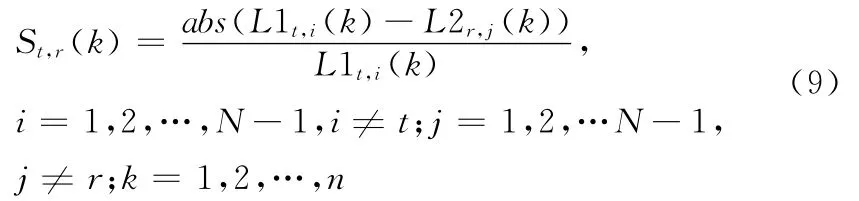
3.3 拓扑相似法关联准则

当计算出描述两航迹接近程度的拓扑相似度之后，下一步就是如何判决两航迹间的相似性。为了给出航迹i（i∈U1）与航迹j（j∈U2）间的相似性判决，需要对拓扑相似度按从大到小进行排序，即得相似序。这里我们采用最大相似度识别原则，即

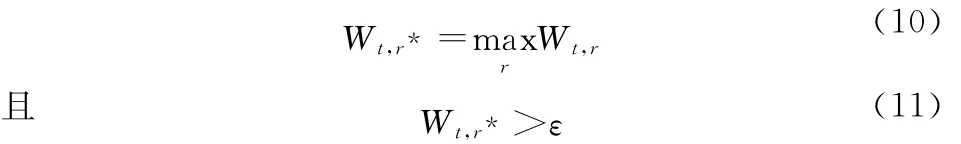
则判决航迹t在l时刻与航迹r＊关联，并且r＊在l时刻不再与其他航迹关联；否则来自局部节点的航迹t在l时刻不与来自局部节点2的任何一条航迹关联。其中ε为阈值参数，0.5≤ε＜1，阈值可以通过仿真来确定。

4 仿真分析

为了讨论问题的方便，这里仅考虑两个局部节点，并且每个局部节点配有一部2D雷达。仿真环境1：雷达测距和测角误差分别为σρ1＝170m，σθ1＝1°，σρ2＝180m，σθ2＝1°用蒙特卡洛方法进行50次仿真，每次仿真14步，采样间隔T＝4s，假设在两传感器的公共观测区域内有60批目标，模拟目标在一个二维平面上具有变速、存在有意和无意机动，具有可以认为在速度上变化的过程噪声，目标初始速度在4m／s～1200m／s之间均匀分布，初始航向在0～2π之间均匀分布，目标初始位置在x＝190km，y＝135km处按正态分布产生，两局部节点的位置分别为（125km，125km）和（235km，130km）。

仿真结果1：

仿真分析1：图3给出了在公共观测区域60批目标的运动轨迹，图4～6分别给出的是对图3所示的公共区域目标的航迹分别采用拓扑相似法和加权法仿真50次后的平均正确关联率、错误关联率和遗漏关联率曲线，由图3可以看出拓扑相似法的正确关联率明显高于加权法，并且它的正确关联率相当的高，几乎趋近于1，由图6可以看出拓扑相似法的漏关联率等于0，而加权法在一定程度上则存在着漏关联率，通过上面的比较，可见拓扑相似法较好的关联性能。

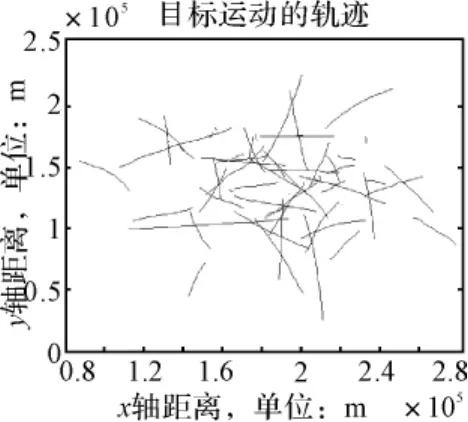
图3 60批目标的运动轨迹

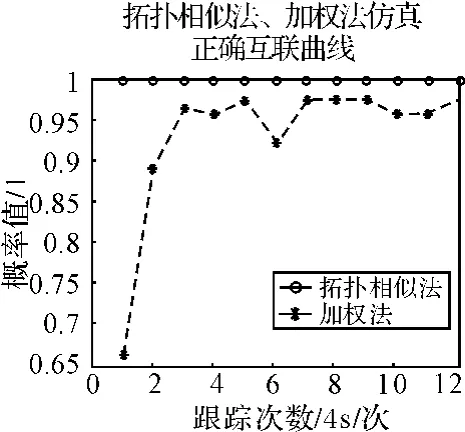
图4 拓扑相似法与加权法正确关联率对比

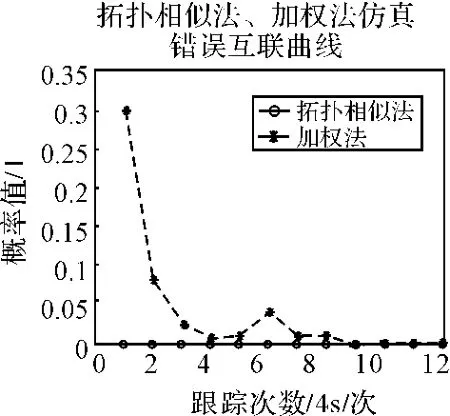
图5 拓扑相似法与加权法错误关联率对比

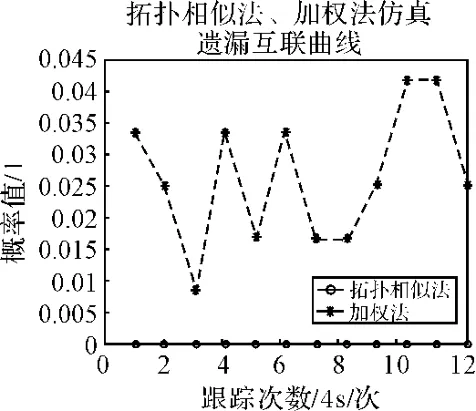
图6 拓扑相似法与加权法漏关联率对比

仿真环境1：雷达测距和测角误差分别为σρ1＝120m，σθ1＝0.6°，σρ2＝110m，σθ2＝0.6°，用蒙特卡洛方法进行50次仿真，每次仿真14步，采样间隔T＝4s，假设在两传感器的公共观测区域内有N＝10批目标，模拟目标在一个二维平面上做匀速直线运动，具有可以认为在速度上变化的过程噪声，目标速度为vx＝600m／s，vy＝600m／s，目标初始位置在x＝165km，y＝115km附近产生，目标之间的间距设为d＝2000m，两局部节点的位置分别为（125km，125km）和（235km，130km）。

在模拟目标运动时，取

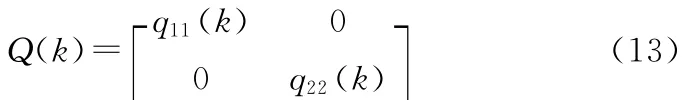
仿真结果2：

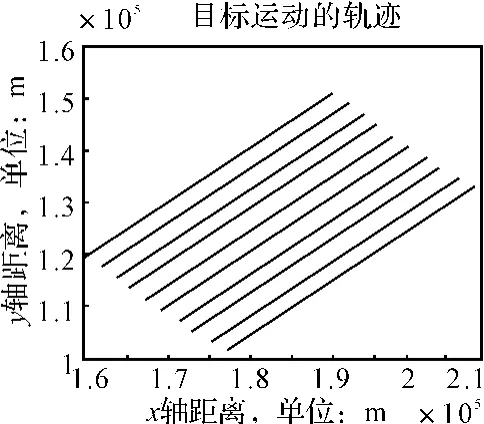
图7 10批目标的运动轨迹

仿真分析2：图7给出了在公共观测区域10批目标的运动轨迹，表1给出了拓扑相似法的正确关联率随目标间距变化情况，从表1可以看出拓扑相似法的正确关联率对目标的间距不敏感，当目标间距变化时，它的正确关联率指标基本保持稳定，只有少量的提升，特别是正确关联率都保持在95%以上，表2给出了拓扑相似法的正确关联率随目标个数变化情况，从表2可以看出拓扑相似法的正确关联率随目标个数的递增有少许的下降，当目标个数达到120时，它的正确关联率仍可以维持在91%以上，说明该算法能够很好的适应密集目标环境，表1和表2综合说明了拓扑相似法较高的关联精度和鲁棒性。

表1 拓扑相似法正确关联率随目标间距变化情况（N＝10）

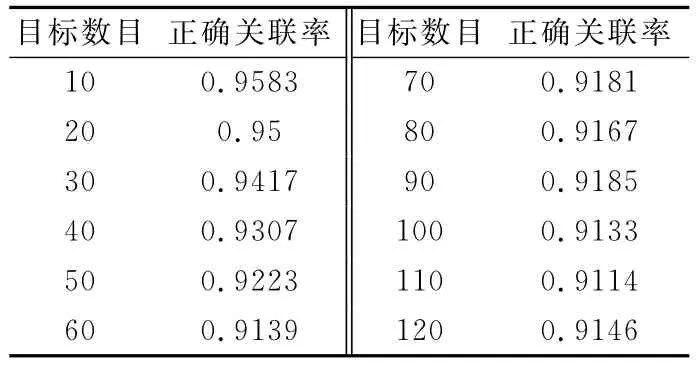
表2 拓扑相似法正确关联率随目标个数变化情况（d＝2000m）

5 结语

目标之间的拓扑关系可以为航迹关联提供更多的有用信息，利用目标拓扑结构这一新的特征进行判决与人工数据关联判决过程非常相似。本文提出了一种基于拓扑相似度的航迹关联算法，该算法充分利用了目标之间的拓扑信息来衡量航迹间接近的程度，避免空间划分不均匀、算法经验性太强、对密集航迹场景不适应等多种问题，仿真结果表明该方法具有很好的有效性和鲁棒性，值得推广。

［1］Bar－Shalom.Y.， William.D.B.， Multitarget－Multisensor Tracking，Applications and Advances［M］.Artech House，2001：225－231.

［2］Bar－Shalom.Y.A Tutorial on Multitarget－Multisensor Tracking and Fusion.1997，IEEE National Radar Conference，15 May 1997，Syracuse，NY：153－156.

［3］Chong，C.－Y.，Mori，S.，Barker，W.H.，and Chang，K.－C.Architectures and algorithms for track association and fusion.IEEE Aerospace and Electronic Systems Magazine，15，1（Jan.2000）：5－13.

［4］Rao，B.S.，and Durrant－Whyte，H.F.Fully decentralized algorithm for multisensor Kalman filtering.IEEE Proceedings，Pt.D，138，5（1991）：413－420.

［5］Bar－Shalom.Y.， William.D.B.， Multitarget－Multisensor Tracking，Applications and Advances［M］.Artech House，2001：155－157.

［6］何友.分布式多传感信息融合算法研究［D］.清华大学，2006.

［7］何友，王国宏，陆大金，等.多传感器信息融合及应用［M］.第二版.北京：电子工业出版社，2000：7－13.

［8］杨哲，韩崇昭，李晨，等.基于目标之间拓扑信息的数据关联方法［J］.系统仿真学报，2008，20（9）：2357－2360.

［9］石玥，王钺，王树刚，等.基于目标参照拓扑的模糊航迹关联方法［J］.国防科技大学学报，2006，28（4）：105－109.

［10］李启元，段立，李亚楠.海战场目标航迹间距离聚类方法［J］.计算机与数字工程，2010（5）.

［11］熊瑜，饶跃东.基于改进蚁群算法的无人飞行器航迹规划［J］.计算机与数字工程，2010（7）.

［12］吴泽民，任姝婕，刘熹.基于拓扑序列法的航迹关联算法［J］.航空学报，2009，30（10）：1937－1942.